La circonferenza
Luoghi geometrici
Luogo geometrico di punti: insieme di tutti e soli i punti che godono della proprietà p.
Un luogo di punti è quindi una figura geometrica F i cui punti hanno le seguenti caratteristiche:
• tutti i punti di F, nessuno escluso, soddisfano p
• non ci sono altri punti oltre a quelli di F che soddisfano p.
ESEMPI DI LUOGHI GEOMETRICI
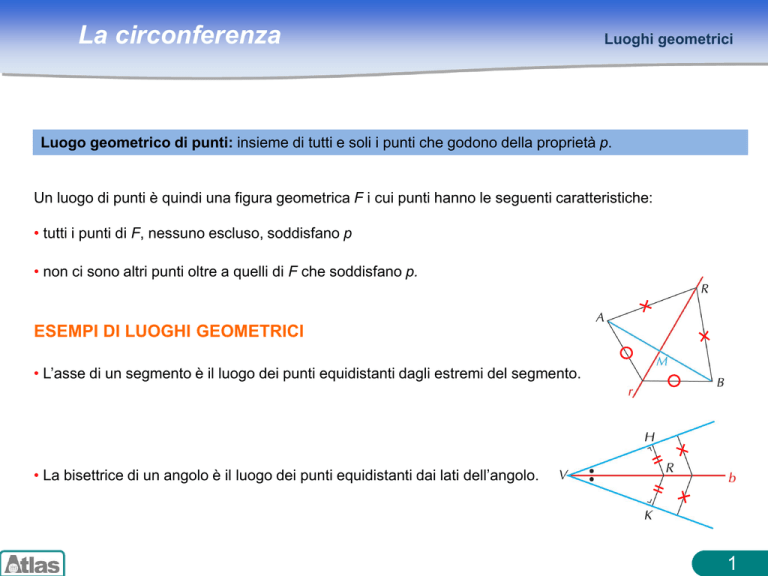
• L’asse di un segmento è il luogo dei punti equidistanti dagli estremi del segmento.
• La bisettrice di un angolo è il luogo dei punti equidistanti dai lati dell’angolo.
1
La circonferenza
Definizione e proprietà
Si chiama circonferenza il luogo dei punti del piano che hanno distanza
costante da un puto fisso assegnato detto centro.
Si chiama cerchio l’insieme dei punti di una circonferenza e dei suoi punti
interni.
La circonferenza e il cerchio sono figure che:
hanno un centro di simmetria
che è esattamente il centro
della circonferenza
hanno infiniti assi di simmetria
rappresentati dalle rette che
passano per il centro
sono unite in ogni rotazione
attorno al centro O
2
La circonferenza
Condizioni per individuare una circonferenza
Per un punto del piano passano infinite circonferenze.
A,B: punti base
Per due punti del piano passano infinite circonferenze.
Retta AB: asse radicale
Retta dei centri: asse centrale
Per tre punti del piano non allineati passa una e una sola circonferenza.
CONSEGUENZE:
due circonferenze distinte non possono avere più di due punti di intersezione; infatti se ne
avessero tre sarebbero la stessa circonferenza
una circonferenza non può avere punti allineati
3
La circonferenza
Elementi della circonferenza e del cerchio
Arco: ciascuna delle due parti in cui due punti (A e B) dividono la circonferenza
Corda: segmento che congiunge due punti della circonferenza
Diametro: corda passante per il centro
Si dice che l’arco AB sottende la corda AB.
Segmento circolare a una base: parte di cerchio delimitata da una corda e da
uno dei due archi che la sottendono.
Segmento circolare a due basi: parte di cerchio delimitata da due corde
parallele (AB e CD).
Caso particolare:
4
La circonferenza
Proprietà delle corde
In ogni circonferenza il diametro è maggiore di qualunque corda non
passante per il centro.
In ogni circonferenza, a corde congruenti corrispondono archi congruenti e
angoli al centro congruenti.
La retta perpendicolare ad una corda e passante per il centro della
circonferenza è asse della corda, dimezza l’arco che sottende ed è bisettrice
dell’angolo al centro corrispondente.
5
La circonferenza
Proprietà delle corde
In una stessa circonferenza (o in circonferenze congruenti) corde congruenti
hanno la stessa distanza dal centro e, viceversa, se due corde hanno uguale
distanza dal centro sono congruenti.
In una stessa circonferenza (o in circonferenze congruenti) se una corda è
maggiore di un’altra, la prima ha minore distanza dal centro della seconda e
viceversa
AB > CD
OH < OK
6
La circonferenza
Elementi della circonferenza e del cerchio e proprietà
Angolo al centro: ha il vertice
nel centro della circonferenza
Settore circolare: parte di cerchio
individuata da un angolo al centro
Si dice che l’angolo al centro ACB insiste sull’arco AB.
In una stessa circonferenza (o in circonferenze congruenti) angoli al centro
congruenti insistono su archi congruenti e viceversa.
In una stessa circonferenza (o in circonferenze congruenti) se due angoli al
centro sono disuguali, l’angolo maggiore insiste sull’arco maggiore e viceversa
7
La circonferenza
Posizioni reciproche tra rette e circonferenze
Teorema. Una circonferenza e una retta hanno al più due punti di intersezione.
Una retta è esterna ad una circonferenza se e solo se la sua distanza d dal
centro è maggiore del raggio r: d > r
Una retta è tangente ad una circonferenza se e solo se la sua distanza d
dal centro è congruente al raggio r: d = r
Una retta è secante rispetto a una circonferenza se e solo se la sua distanza d dal
centro è minore del raggio r: d < r
8
La circonferenza
Posizioni reciproche tra rette e circonferenze
Proprietà delle rette tangenti. Se da un punto P esterno ad una circonferenza si mandano le
tangenti alla circonferenza stessa, i segmenti di tangente sono congruenti e la semiretta di origine P
che passa per il centro è bisettrice dell’angolo formato dalle tangenti.
PA ≅ PB
APC ≅ BPC
9
La circonferenza
Posizioni reciproche tra circonferenze
Anche due circonferenze distinte non possono avere più di due punti di intersezione.
Indichiamo con d la distanza tra i centri di due circonferenze distinte e con r e r’ (con r > r’) i due
raggi.
Le circonferenze sono:
• esterne se e solo se d > r + r’
• tangenti esternamente se e solo se d ≅ r + r’
In questo caso le circonferenze sono entrambe tangenti alla retta t e hanno altre due tangenti in
comune (le rette in giallo in figura).
• secanti se e solo se r – r’ < d < r + r’
10
La circonferenza
Posizioni reciproche tra circonferenze
• tangenti internamente se e solo se d ≅ r - r’
In questo caso le circonferenze sono entrambe tangenti alla retta t ma non hanno altre tangenti comuni.
• interne se e solo se d < r − r’
• concentriche se e solo se d = 0
11
La circonferenza
Angoli alla circonferenza e angoli al centro
Si dice angolo alla circonferenza un angolo che ha il vertice sulla circonferenza e i lati o entrambi
secanti oppure uno secante e l’altro tangente (o entrambi tangenti) alla circonferenza.
AVB insiste sull’arco AB
(in rosso)
EPD insiste sull’arco EP
(in rosso)
All’angolo AVB alla circonferenza che insiste sull’arco AB possiamo
associare l’angolo al centro ACB che insiste sullo stesso arco. Esso si
costruisce tracciando le semirette che hanno origine nel centro della
circonferenza e passano per A e B
Teorema. Ogni angolo alla circonferenza è la metà del corrispondente angolo al centro.
12










