circuito puramente ohmico

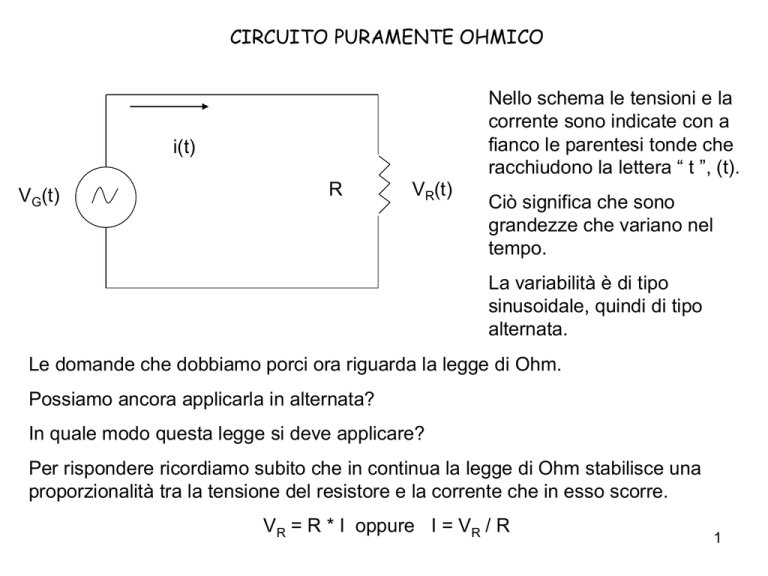
CIRCUITO PURAMENTE OHMICO
Nello schema le tensioni e la
corrente sono indicate con a
fianco le parentesi tonde che
racchiudono la lettera “ t ”, (t).
i(t)
VG(t)
R
VR(t)
Ciò significa che sono
grandezze che variano nel
tempo.
La variabilità è di tipo
sinusoidale, quindi di tipo
alternata.
Le domande che dobbiamo porci ora riguarda la legge di Ohm.
Possiamo ancora applicarla in alternata?
In quale modo questa legge si deve applicare?
Per rispondere ricordiamo subito che in continua la legge di Ohm stabilisce una
proporzionalità tra la tensione del resistore e la corrente che in esso scorre.
VR = R * I oppure I = VR / R
1
CIRCUITO PURAMENTE OHMICO
Nel seguente grafico rappresentiamo l’andamento di una corrente “ I “ che
scorre nel resistore “ R “ e cerchiamo di calcolare la tensione VR che si
produce ai suoi capi.
i
+2
+3
+1
+2
+1
t7
t8
t9
t1
T
t11
0
t1
t2
t3
t4
t5
t6
-1
-2
-1
-3
-2
Possiamo immaginare che la corrente variabile sia costituita in realtà da tantissimi
(infiniti !) valori di corrente continua, che cambiano tutti continuamente ad ogni istante
che passa. Nel grafico ne abbiamo disegnati solo alcuni.
Consideriamo l’istante t=0 quando la corrente vale zero. Applicando la legge di Ohm
anche la tensione su R sarà zero.
VR (0)= R * i(0) = R*0 = 0 V
2
CIRCUITO PURAMENTE OHMICO
Continuando con il ragionamento si ottengono tutti gli altri valori per ogni istante
di tempo.
t1 : VR (t1)= R * (+1) V
t2: VR (t2)= R * (+2) V
t3 : VR (t3)= R * (+3) V ecc.
…..
t7 : VR (t7)= R * (-1) V
t8 : VR (t8)= R * (-2) V
t9 : VR (t9)= R * (-3) V ecc.
….
Come si vede il grafico della tensione VR avrà in ogni istante il valore della
corrente moltiplicato per un fattore costante R, la resistenza.
Quindi la forma sinusoidale non cambierà, mentre il valori assunto si dovrà
calcolare, come abbiamo fatto sopra, con la legge di Ohm.
3
CIRCUITO PURAMENTE OHMICO
Facciamo un esempio numerico. Supponiamo che R = 10 W, troveremo che i
valori di VR, per ogni istante di tempo saranno i seguenti.
t1 : VR (t1) = 10 * (+1) V = 10 V
t2 : VR (t2) = 10 * (+2) V = 20 V
t3 : VR (t3) = 10 * (+3) V = 30 V ecc.
…..
t7 : VR (t7) = 10 * (-1) V = - 10 V
t8 : VR (t8) = 10 * (-2) V = - 20 V
t9 : VR (t9) = 10 * (-3) V = - 30 V ecc.
….
Il grafico risultante sarà il seguente.
VR
+20
+30
+10
+20
+10
t7
t8
t9
t1
T
t11
0
t1
t2
t3
t4
t5
t6
-10
-20
-10
-30
-20
4
CIRCUITO PURAMENTE OHMICO
Dal ragionamento fatto sembrerebbe che per conoscere la tensione VR ( ma anche la
corrente “ I ”, con la formula inversa) si debbano effettuare “infiniti” calcoli, cioè uno per
ogni istante di tempo.
Naturalmente questo non è possibile, quindi occorrerà affrontare il problema con un
altro ragionamento.
Osserviamo le due sinusoidi che rappresentano la corrente “ I “ e la tensione “ VR ”.
+3
i
+2
+2
+1
+1
T
t7
t8
t9
t1
t11
0
t1
t2
t3
t4
t5
t6
-1
VR
+20
+30
+10
-2
-1
-3
-2
+20
+10
t7
t8
t9
t1
t11
0
t1
t2
t3
t4
t5
t6
-10
-20
-10 5
-30
-20
T
CIRCUITO PURAMENTE OHMICO
Osserviamo che entrambe partono all’istante t=0 dal valore zero.
Entrambe raggiungono il valore massimo all’istante t3 ( cioè T/ 4).
Entrambe ritornano al valore zero all’istante t6 ( cioè T/ 2). Ecc.
Sappiamo che tale comportamento è tipico delle sinusoidi in fase.
Sappiamo anche che le sinusoidi si possono rappresentare facilmente con i
vettori.
Quindi possiamo disegnare due vettori, uno per la corrente “ I “ ed uno per la
tensione “ VR “ che rappresentino le due sinusoidi.
I due vettori disegnati hanno una lunghezza che rappresenta il valore massimo
(ampiezza della sinusoide) o della corrente o della tensione. Non bisogna quindi
fare dei paragoni tra le due lunghezze, poiché sono grandezze non omogenee
per le quali si può scegliere anche due scale diverse.
Domanda: perché entrambi sono
disegnati orizzontalmente?
I
VR
Se guardiamo la prossima figura ci
ricorderemo che in questo modo si
origineranno due sinusoidi in fase.
6
CIRCUITO PURAMENTE OHMICO
I
VR
7
CIRCUITO PURAMENTE OHMICO
Dall’osservazione dei vettori e delle sinusoidi possiamo trarre la conclusione
che possiamo fare il calcolo della legge di Ohm solo una volta, cioè
utilizzando solo con il valore assunto dal vettore (ampiezza) e disegnando i
vettori nella loro giusta relazione di fase.
Siccome dallo studio appena fatto abbiamo ricavato che corrente e tensione
per una resistenza risultano in fase, disegneremo due vettori paralleli.
I
VR
I due vettori si possono disegnare
anche sovrapposti, come
normalmente si fa.
8
CIRCUITO PURAMENTE OHMICO
Possiamo concludere lo studio di questo circuito dicendo che la formula della
legge di Ohm è ancora valida anche in alternata, però diventa una relazione tra
vettori. Quindi essa si dovrà scrivere facendo attenzione alla notazione grafica:
VR  RI
VR
I
R
Si definisce anche l’inverso della resistenza, che prende nome di
conduttanza G. Essa si misura in “siemens” = S.
G = 1/ R (S)
9
CIRCUITO PURAMENTE INDUTTIVO
ALCUNI SOLENOIDI (O INDUTTORI, O BOBINE)
10
CIRCUITO PURAMENTE INDUTTIVO
i(t)
VG(t)
L
VL(t)
2
N S
H 
L
l
INDUTTANZA o coefficiente di
autoinduzione (si misura in Henry = H)
Lo studio di questo circuito si effettua partendo dalla legge di Faraday-Neumann-Lenz
Nelle diapositive seguenti si farà un riepilogo del magnetismo già studiato al terzo
anno, ricordando le grandezze fisiche più importanti, che serviranno al nostro studio.
11
CIRCUITO PURAMENTE INDUTTIVO
Paragonando le due figure
risulta che un magnete
naturale (calamita in alto) e un
solenoide percorso da
corrente continua (in basso)
producono le stesse linee di
forza del campo magnetico H.
Si deduce che una corrente
continua genera una campo H.
H è in relazione con il campo
B (induzione magnetica)
secondo la formula: B =  H.
 permeabilità magnetica.
Infine il flusso f ci definisce
quanto campo B attraversa il
solenoide si sezione S.
f BS
f = Li
12
CIRCUITO PURAMENTE INDUTTIVO
Notiamo il modo di indicare il Nord ed il Sud prodotti dal campo magnetico H.
Per “convenzione” si indica il Nord magnetico dove “escono” le linee di forza di H (nel
disegno a destra), mentre il Sud dove rientrano le stesse linee (nel disegno a
sinistra).
Per individuare rapidamente i due poli si può adottare la regola delle dita della mano destra
(eccetto il pollice) che afferrano il solenoide con le punte dirette come la corrente. Il pollice 13
fornisce il Nord.
CIRCUITO PURAMENTE INDUTTIVO
Cosa succede se facciamo variare il flusso nel solenoide? Controlliamo le
seguenti figure.
L’esperienza a lato ci
mostra che nel solenoide
scorre una corrente per
tutto il tempo in cui il flusso
varia.
Possiamo notare anche
che il verso della corrente
cambia se invertiamo il
verso del movimento della
calamita.
Nelle figure il galvanometro
registra l’intensità ed il
verso delle correnti.
Come è evidente questa
corrente non è generata da
un generatore ma dal
movimento della calamita.
14
CIRCUITO PURAMENTE INDUTTIVO
Movimento!!
15
CIRCUITO PURAMENTE INDUTTIVO
Movimento!!
(2)
16
CIRCUITO PURAMENTE INDUTTIVO
17
CIRCUITO PURAMENTE INDUTTIVO
18
CIRCUITO PURAMENTE INDUTTIVO
Dall’esperienza appena illustrata possiamo ricavare che l’energia cinetica della
calamita si trasforma in energia elettrica (la corrente). Il fenomeno in fisica è noto
poiché l’energia non si può distruggere (si conserva), ma si può trasformare in una
di altra forma. Come conseguenza di ciò si può dedurre che se la calamita si ferma
non scorrerà corrente (poiché non c’è energia da trasformare!).
Dalle due figure precedenti si può notare un altro importantissimo fenomeno.
Nella figura di sinistra la spira genera un flusso che esce verso sinistra, dove quindi
si forma un altro nord (N’). Nella figura di destra invece la spira genera un flusso che
esce verso destra e quindi le polarità sono generate al contrario.
La conclusione è che la spira di sinistra “tende” a respingere la calamita, mentre la
spira di destra “tende” ad attrarla.
19
CIRCUITO PURAMENTE INDUTTIVO
Quali conclusioni si possono trarre dalle considerazioni precedenti ?
1° caso: dato che la calamita si
avvicina, il flusso che attraversa il
solenoide è in aumento. Notiamo che il
solenoide “reagisce” cercando di non far
aumentare il flusso (infatti N’ respinge la
calamita). Questo fenomeno è
denominato “induzione”, poiché il
solenoide viene indotto a contrastare
l’aumento di flusso.
2° caso: dato che la calamita si
allontana, il flusso che attraversa il
solenoide è in diminuzione. Notiamo
che il solenoide “reagisce” cercando di
non far diminuire il flusso (infatti S’ attira
la calamita). Anche ora il solenoide
viene indotto a contrastare la
diminuzione di flusso.
20
CIRCUITO PURAMENTE INDUTTIVO
Utilizzando ancora il principio di conservazione dell’energia dobbiamo attenderci che
se la calamita viene mossa più velocemente (in avvicinamento o in allontanamento
al solenoide) e quindi con una maggiore energia cinetica, questa deve generare una
corrente indotta che varia più velocemente.
In effetti questo è proprio quello che accade.
Riepiloghiamo i risultati ottenuti:
1.Se il flusso fe va aumentando il solenoide “genera” una corrente “indotta”
che provoca un altro flusso interno “indotto” fi che si sottrae a fe nel
tentativo di bloccarne l’aumento.
2.Se il flusso fe va diminuendo il solenoide “genera” una corrente “indotta” che
provoca un altro flusso interno “indotto” fi che si somma a fe nel tentativo di
bloccarne la diminuzione.
3.Se i flussi variano più velocemente (in aumento o in diminuzione) le correnti indotte
ed i flussi indotti sono di ampiezza maggiore.
21
CIRCUITO PURAMENTE INDUTTIVO
A questo punto possiamo anche sostituire la calamita che si sposta con un altro
solenoide. Esso genera un flusso che per un intervallo di tempo aumenta ed in un
altro diminuisce. Questo flusso viene inviato al solenoide che avevamo
precedentemente collegato alla calamita. Il risultato è assolutamente identico.
22
CIRCUITO PURAMENTE INDUTTIVO
Possiamo ora analizzare il comportamento del circuito iniziale. Al posto della
calamita esterna ora c’è un generatore che fornisce una corrente I(t) che origina il
flusso esterno fe. Il solenoide quindi si comporterà come quello sottoposto alle
variazioni di flusso della calamita.
Lo studio analitico si base sulla
legge di Faraday – Neumann - Lenz
i(t)
VG(t)
L
VL

i
 L
VL 
t
t
Significato dei simboli matematici:
1. VL = tensione indotta sul solenoide
2.   flusso
3. i = variazione di corrente
4.   L* i = variazione di flusso
5. t = intervallo di tempo
23
CIRCUITO PURAMENTE INDUTTIVO
Esempio: il flusso varia da (t1) = 0 Wb a (t2) = 50 mWb; t = t2 – t1 = 0,01 s.
10 mH. Quanto vale VL e i ?
L=
Calcolo:
  (t2) - (t1) = 50-0 = 50 mWb= 50*10-3 Wb =5*10-2 Wb
VL = (5*10-2)/0,01=5 V
i(t1)= (t1) / L = 0/10 = A
i(t2)= (t2) / L =50/10 = 5 A
i = i(t2) - i(t1) = 5 – 0 = 5 A
Lo stesso risultato si ottiene con la formula (identica alle precedenti, ma più veloce):
i = /L = (50*10-3) / (10*10-3) = 5 A
24
CIRCUITO PURAMENTE INDUTTIVO
Ricaviamo ora un diagramma vettoriale del circuito puramente induttivo,usato per
tutti i calcoli e per tutti gli studi su questo circuito.
Siccome il circuito sarà utilizzato in regime sinusoidale non è possibile studiarlo
con la matematica necessaria, poiché non si hanno le conoscenze adeguate.
Si userà una versione semplificata per raggiungere lo stesso risultato.
Consideriamo la seguente forma d’onda per la corrente “i” che somiglia
abbastanza ad una sinusoide. I valori sono uguali a quelli dell’esempio
precedente.
i (A)
5
50
0
10
30
40
70
t (ms)
80
-5
25
CIRCUITO PURAMENTE INDUTTIVO
La corrente aumenta da 0 A a 5 A in 10 ms. Il solenoide si oppone a tale
variazione e quindi genera una corrente indotta in verso opposto. VL =
5V
1
i (A)
VL (V)
5
+
t (ms)
+
i(t)
L
VG
5
VL
iI
t (ms)
10
0
10
0
La corrente non varia. Il solenoide non deve opporsi a variazioni di
corrente e quindi non genera correnti indotte. VL = 0 V
2
i (A)
VL (V)
5
i(t)
VG
L
VL
t (ms)
0
10
30
t (ms)
0
10
30
26
CIRCUITO PURAMENTE INDUTTIVO
3
i (A)
5
t (ms)
10
0
VL = - 5 V
40
30
La corrente diminuisce da 5 A a 0 A in
10 ms. Il solenoide si oppone a tale
variazione e quindi genera una
corrente indotta nello stesso verso.
+
VG
i(t)
L
VL
iI
+
VL(V)
30
0
40
t (ms)
10
-5
27
CIRCUITO PURAMENTE INDUTTIVO
4
In questo intervallo la corrente ha un
valore negativo, quindi significa che
va inverso opposto a quella vista fio
ad ora.
i (A)
50
10
0
30
La corrente aumenta da 0 A a - 5 A in
10 ms. Il solenoide si oppone a tale
variazione e quindi genera una
corrente indotta in verso opposto.
t (ms)
40
-5
VL = - 5 V
VL(V)
i(t)
40
L
VG
+
VL
iI
0
50
t (ms)
+
-5
28
CIRCUITO PURAMENTE INDUTTIVO
5
i (A)
5
50
70
0
t (ms)
La corrente non varia. Il
solenoide non deve opporsi
a variazioni di corrente e
quindi non genera correnti
indotte. VL = 0 V
-5
VL (V)
i(t)
VG
L
VL =0
50
0
70
t (ms)
29
CIRCUITO PURAMENTE INDUTTIVO
6
i (A)
70
80
0
t (ms)
-5
La corrente diminuisce da
- 5 A a 0 A in 10 ms. Il
solenoide si oppone a tale
variazione e quindi genera
una corrente indotta nello
stesso verso.
VL = + 5 V
+
i(t)
L
VG
+
VL
iI
VL (V)
+5
70
0
80
t (ms)
30
CIRCUITO PURAMENTE INDUTTIVO
Riepiloghiamo i risultati riportando i grafici sia della corrente che della tensione.
i (A)
5
50
0
10
30
40
70
t (ms)
80
-5
VL (V)
+5
0
-5
t (ms)
31
CIRCUITO PURAMENTE INDUTTIVO
Dal risultato ottenuto in
precedenza possiamo
immediatamente ricavarne
un altro se abbiamo una
corrente triangolare.
“ i ” = costante
i (A)
5
30
0
10
40
t (ms)
20
-5
VL (V)
“ i ” = costante
+5
t (ms)
L’osservazione che
possiamo fare riguarda
la corrente “i” che non è
mai costante. Infatti ci
sono solo due punti
dove, per un solo istante,
la corrente non varia.
Questi istanti solo 10 e
30. In questi due solo
istanti la tensione VL vale
zero
0
-5
32
CIRCUITO PURAMENTE INDUTTIVO
Osserviamo ora i seguenti grafici delle correnti e calcoliamo con la legge di
Faraday – Neumann – Lenz la tensione ai capi del solenoide, usando i valori
precedenti. (L = 10 mH)
Pendenza
minore
i (A)
i (A)
Pendenza
maggiore
5
5
t (ms)
t (ms)
0
10
V L  L
i
5
 10 103
 5V
3
t
10 10
Tensione
maggiore
VL (V)
0
10
20
V L  L
i
5
 10 103
 2,5V
t
20 103
Tensione
minore
VL (V)
5
2,5
t (ms)
t (ms)
10
20
33
CIRCUITO PURAMENTE INDUTTIVO
La deduzione derivante dall’esempio precedente è che se la corrente varia
della stessa quantità ( la corrente aumenta o diminuisce di 5 A) ma essa
avviene in più tempo ( occorrono 20 ms e non 10 ms), la tensione indotta
nel solenoide diminuisce. Questo si ricava anche matematicamente la legge
di Faraday – Neumann – Lenz in cui la tensione VL è inversamente
proporzionale alla variazione di tempo t.
Il risultato si può interpretare geometricamente, dicendo che se la pendenza
della corrente è minore, risulta minore anche la tensione indotta VL.
Al contrario se la pendenza della corrente è maggiore, risulta maggiore
anche la tensione indotta VL.
Queste due ultime considerazioni sono coerenti con l’osservazione fisica già
fatta in precedenza.
Cioè una pendenza maggiore significa una corrente che varia più
velocemente e quindi che dall’esterno si sta fornendo più energia cinetica (la
calamita che si allontana o si avvicina più rapidamente).
34
CIRCUITO PURAMENTE INDUTTIVO
Consideriamo una corrente che varii in modo più complesso e con le regole stabilite
disegniamo la tensione indotta VL.
i (A)
10
5
70
0
10
30
50
90
110
120
60
t (ms)
-5
-10
VL(V)
5
2,5
50 60 70
0
10
30
t (ms)
90
110
L’osservazione dei due grafici,
disegnati seguendo la legge di
Faraday – Neumann – Lenz,
mostra che quando la pendenza
della corrente è maggiore la
tensione assume un valore
maggiore, quando invece la
pendenza della corrente è
minore la tensione assume un
valore minore.
Questa proprietà si può ora
applicare alle sinusoidi e
verificare che anche per esse è
verificata la stessa regola.
120
- 2,5
-5
35
CIRCUITO PURAMENTE INDUTTIVO
10
8
6
4
2
0
0
0,005
0,01
0,015
0,02
0,025
-2
-4
-6
-8
-10
Notare come a pendenza maggiore di “I” corrisponda una tensione “V”
maggiore.
36
CIRCUITO PURAMENTE INDUTTIVO
10
8
6
4
2
0
0
0,005
0,01
0,015
0,02
0,025
-2
-4
-6
-8
-10
37
CIRCUITO PURAMENTE INDUTTIVO
Lenz
I
I,V
10
8
6
4
V
L
2
t
0
0
0,005
0,01
0,015
0,02
0,025
-2
-4
-6
-8
-10
38
CIRCUITO PURAMENTE INDUTTIVO
Dall’ultimo grafico corrente – tensione si ricava che queste due sinusoidi sono
sfasate di 90°, cioè V ed I sono in quadratura.
Quindi per rappresentare vettorialmente questa situazione si disegnano due vettori
come di seguito.
VL (5 V)
90°
Si deduce che la tensione VL è in
anticipo di 90° sulla corrente I.
I (10 A)
Oppure la corrente I è in ritardo di
90° sulla tensione VL
39
CIRCUITO PURAMENTE INDUTTIVO
Adesso dobbiamo chiederci se tra tensione e corrente sia ancora valida la
legge di OHM.
Come si è visto prima i vettori tensione e corrente sono vettori sfasati di 90°,
quindi possiamo rappresentarli sul piano di Gauss, come di seguito.
I = 10 A
VL = j 5 V
Im
j5
VL (5 V)
Re
10
I (10 A)
Secondo la legge
di OHM deve
esistere una
grandezza
elettrica che ci
misura la difficoltà
della corrente a
circolare nel
solenoide.
In questo caso la
grandezza si
chiamerà
REATTANZA
INDUTTIVA “ XL “.
40
Circuito puramente induttivo
La reattanza induttiva
I = 10 A
VL = j 5 V
V L j5

 j 0,5W
XL 
I
10
Dalla legge di Faraday – Neumann – Lenz è possibile ricavare l’espressione
matematica della reattanza induttiva.
i
V L  L
t
Notiamo che VL è sicuramente proporzionale all’induttanza L che è una costante
derivante dalla forma geometrica del solenoide ed anche dal materiale
magnetico usato.
Inoltre la tensione VL dipenderà da un altro fattore di seguito discusso.
41
Circuito puramente induttivo
La reattanza induttiva
V L  L
i
t
In questa formula c’è una operazione chiamata “derivata”, che si studierà il prossimo
anno. Quindi non è adesso possibile effettuare il calcolo seguendo le regole della
matematica. Possiamo fare delle considerazioni fisiche per giustificare la formula
della reattanza induttiva.
1. Se la corrente varia velocemente (pendenza elevata) anche la tensione deve
aumentare; abbiamo trovato che ciò si accorda con il principio di conservazione
dell’energia)
2. In una sinusoide la velocità è data dalla pulsazione
essere proporzionale ad essa.
w, quindi la tensione deve
Possiamo quindi scrivere la formula finale che lega la tensione VL alla corrente I.
( 
Ricordiamo che un vettore moltiplicato per “ j “ ruota di 90° antiorario.
V L  w  L  jI
V L  jw  L  I
V L  ( jw  L   I
Quindi se moltiplichiamo “ I “ per “ j “
otteniamo un vettore in fase con VL
42
Circuito puramente induttivo
La reattanza induttiva
Formula finale tra la tensione VL e corrente I.
V L  ( jw  L   I
Da questa formula si ricava la reattanza induttiva
(
j  w  L I
V
L

 j w  L
XL 
I
I
X L  j  w  L (W)
XL è sempre positiva !!
L’inverso della reattanza induttiva si chiama “suscettanza induttiva” BL e si misura in
“siemens” = S (W -1)
BL = 1/ XL
43
Circuito puramente induttivo
Riepilogo
Lenz
I,V
10
La tensione VL è in anticipo di 90°
sulla corrente I.
I
8
6
4
2
t
0
0
0,005
0,01
0,015
0,02
0,025
-2
Oppure la corrente I è in ritardo di
90° sulla tensione VL
-4
-6
-8
V
-10
V L  ( jw  L   I
VL
90°
X L  j  w  L (W)
I
44
Circuito puramente capacitivo
45
Circuito puramente capacitivo
46
Circuito puramente capacitivo
Tutte le volte che due parti di
materiale conduttore (che
chiameremo armature) vengono a
trovarsi vicine e separate da materiale
isolante (o dielettrico), si ha un
condensatore.
La carica è immagazzinata sulla superficie delle piastre, sul bordo a contatto
con il dielettrico. Poiché ogni piastra immagazzina una carica uguale ma di
segno opposto una rispetto all'altra, la carica totale nel dispositivo è sempre
zero. L'energia elettrostatica che il condensatore accumula si localizza nel
materiale dielettrico che è interposto fra le armature.
47
Circuito puramente capacitivo
Per valutare se un condensatore è in grado di accumulare una quantità più o meno
grande di carica si definisce la grandezza “capacità” C, la cui unità di misura è il
Farad (F).
Q
C
V C
Questa formula si può interpretare fisicamente considerando il
condensatore come un recipiente che contiene cariche.
Se a due condensatori diversi facciamo variare la tensione
della stessa quantità (per es.: 1 V), di quanto varia la carica?
Cioè fissiamo VC = 1 V, avremo che Q = C*VC = C.
Quindi possiamo concludere che la capacità è la variazione
della quantità di carica, quando la tensione varia di 1 V.
A
B
Un paragone idraulico semplice consiste nel prendere due
recipienti diversi e versare in entrambi una quantità d’acqua
che innalzi il livello di 1 cm (variazione di tensione). Allora il
recipiente che avrà aumentato maggiormente il suo volume
(cioè la carica) avrà una capacità maggiore.
48
Circuito puramente capacitivo
Alcune considerazioni fisiche con il paragone idraulico ci faranno comprendere il
comportamento del condensatore.
A
B
Supponiamo di versare dell’acqua nel recipiente, il livello
raggiungerà quello prefissato (diciamo 1 cm) dopo alcuni secondi.
Concludiamo quindi che all’istante t=0 si ha la corrente massima
(poiché chi versa l’acqua ha interesse a fare il più in fretta
possibile, salvo a diminuire il flusso quando si sta raggiungendo il
livello stabilito) e il livello sarà zero. Quando invece si sarà giunti
al livello stabilito la corrente diverrà zero.
Queste considerazioni si possono riassumere con le curve che
rappresentano la carica di un condensatore.
49
Circuito puramente capacitivo
Dai grafici della tensione e della corrente si è in grado di ricavare una
informazione: quando la corrente è massima allora la corrente è zero; viceversa
quando la tensione è massima allora la corrente è zero.
La conclusione di tutto ciò è che per caricare un condensatore è indispensabile
che arrivi prima la corrente, quando la tensione è zero, e successivamente
quando la tensione è arrivata al suo valore massimo, la corrente si azzeri.
Si può già disegnare vettorialmente questa situazione, facendo
successivamente una dimostrazione più rigorosa.
I
La corrente I è in anticipo di 90° sulla tensione,
oppure la tensione è in ritardo di 90° sulla corrente.
VC
50
Circuito puramente capacitivo
Facciamo adesso una considerazione sul tempo impiegato dal condensatore per
caricarsi.
Supponiamo di volere aumentare la carica del condensatore della quantità
C in un tempo t = 1 s.
Q = 1
Successivamente aumentiamo ulteriormente la carica del valore Q = 1 C ma in un
tempo molto più piccolo, per esempio t = 1/10 s = 0,1 s.
È intuitivo ricavare che le cariche debbano arrivare più velocemente!!!
In effetti il concetto di corrente elettrica è proprio questo: quantità di carica (positiva!)
che attraversa o arriva in un certo punto nell’unità di tempo (cioè in un secondo).
Ricordiamo allora la formula della corrente:
Q
i
t
Si può affermare che se la corrente “ i ” che sta caricando il condensatore è
grande, il tempo che occorre per la carica è piccolo (cioè corrente e tempo sono
inversamente proporzionali).
51
Circuito puramente capacitivo
Ritorniamo adesso al paragone idraulico considerando il solito recipiente da riempire
d’acqua fino ad un certo livello H (che corrisponde alla tensione VC del
condensatore).
Possiamo avere le seguenti due situazioni:
1. L’altezza H si raggiunge in poco tempo (t piccolo) : l’acqua deve essere versata
con un tubo di sezione grande (portata grande = corrente grande);
2. L’altezza H si raggiunge in molto tempo (t grande) : l’acqua deve essere
versata con un tubo di sezione piccola (portata piccola = corrente piccola);
Concludiamo questo esempio, adattandolo ai condensatori che
lavorano in regime sinusoidale, dicendo che:
1. la corrente è grande se occorre aumentare la tensione
velocemente, cioè se t è piccolo;
H
2. la corrente è piccola se occorre aumentare la tensione
lentamente, cioè se t è grande;
La corrente, quindi, è proporzionale alla velocità (w) di carica
52
del condensatore.
Circuito puramente capacitivo
La formula della capacità si può scrivere anche nel modo seguente.
Q
C
V C
Q  C   V C
dividendo primo e secondo membro per l' intervallo di tempo t si ha :
Q
V C
C
t
t
V C
i C
t
L’ultima formula è molto simile alla legge di Faraday – Neumann – Lenz,
con la differenza dello scambio di posto tra tensione e corrente.
Possiamo quindi dedurre immediatamente che il condensatore si comporta
esattamente al contrario del solenoide.
Avremo quindi che la corrente I è in anticipo sulla tensione VC.
53
Circuito puramente capacitivo
Riportiamo di seguito i due risultati raggiunti finora:
1. La corrente I è proporzionale alla velocità ( w) di carica del condensatore;
2. La corrente I è in anticipo sulla tensione VC
Dal secondo punto possiamo quindi ricavare il diagramma vettoriale per il
condensatore.
I
La corrente I è in anticipo
sulla tensione VC di 90°
VC
Dal primo punto possiamo la legge di Ohm per i condensatori.
Ricordiamo che per le sinusoidi, e per i vettori, la velocità angolare è w, alla
quale è proporzionale la corrente I.
54
Circuito puramente capacitivo
Possiamo quindi scrivere la formula finale che lega la tensione VC alla corrente I.
Ricordiamo che un vettore moltiplicato per “ j “ ruota di 90° antiorario.
Quindi se moltiplichiamo “ VC “ per “ j “ otteniamo un vettore in fase con “I”.
In formule la legge di Ohm per i condensatori si scrive:
(
I  w  C  j V C

I  j  w  C V C
I
j w  C
VC
 1 
  I
V C  
 j w  C 
1

XC
j w  C
1  1 
 I
V C  
j  w C 
XC si chiama REATTANZA
CAPACITIVA e si misura in
W.
 1 
 I
V C   j 
 w C 
La formula è una delle due
sotto riportate (ovviamente
equivalenti).
 j 
 I
VC  
 w C 
VC  XCI
XC 
1
j w  C
j
XC 
w C
XC è sempre negativa !!
55
Circuito puramente capacitivo
L’inverso della reattanza capacitiva si chiama “suscettanza capacitiva” BC e si
misura in “siemens” = S (W -1)
BC = 1/ XC
56