Programma dell’insegnamento di
Geometria e Algebra
a.a. 2013-2014
Prof. Raguso Grazia
Finalità del corso
Il corso intende fornire elementi di calcolo matriciale e vettoriale fondamentale in matematica,
fisica, informatica e scienze applicate, ed elementi di base di Geometria analitica di grande ausilio
nel mondo scientifico..
Il corso prevede lezioni ed esercitazioni tradizionali affiancate ad attività di tutoraggio.
Modalità di esame: Esame orale finale preceduto da valutazioni in itinere.
PROGRAMMA:
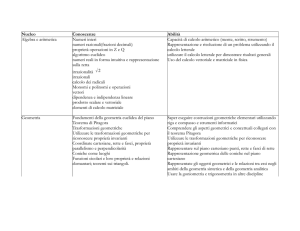
Introduzione all’algebra lineare
Matrici. Operazioni tra matrici. Matrici quadrate. Determinante di una matrice. Rango di una
matrice. Moltiplicazione righe per colonne. Proprietà del determinante. Teorema di Laplace.
Matrice inversa di una matrice non singolare. Rango o caratteristica di una matrice. Sistemi lineari.
Teorema di Cramer. Teorema di Capelli. Sistemi lineari parametrici.
Geometria
Geometria analitica nel piano. Proprietà affini e metriche. Fasci di rette. Relazione di ortogonalità
tra rette. Asse di un segmento. Bisettrice di un angolo. La circonferenza e le sue proprietà. Coniche
come luoghi geometrici. Invarianti di una conica. Equazioni canoniche.Coniche di rango1,2 e 3.
Geometria nello spazio. Riferimento metrico. Distanza tra due punti. Punto medio.
Rappresentazione del piano e fasci di piani. La retta e sue rappresentazioni analitiche. Parallelismo
ed ortogonalità tra rette. Rette sghembe. Minima distanza e retta di minima distanza.
Le superfici di rotazione: coni e cilindri. Piano ampliato con la retta impropria. Piano improprio.
Spazio ampliato. Coordinate omogenee. Le quadriche di rango 1, 2, 3 e 4.
Algebra lineare( continuazione)
Spazi vettoriali: Definizione di sottospazio vettoriale. Combinazione lineare. Vettori linearmente
dipendenti ed indipendenti. Basi di uno spazio vettoriale. Dimensione di uno spazio vettoriale. Lo
spazio vettoriale R n . Isomorfismo tra uno spazio vettoriale di dimensione n ed R n . Basi canoniche.
Applicazioni lineari e loro rappresentazione analitica. Ker f e Im f di un’applicazione lineare f.
Teorema del rango. Endomorfismo, autovalori ed autovettori. Diagonalizzazione di una matrice.
Testi consigliati:
-A. Sanini, Elementi di Geometria, con esercizi – Editrice Levrotto & Bella, Torino.
-G.Raguso, M. Tucci, Nozioni elementari di algebra lineare, Appendice del Calcolo differenziale 1
di R. Adams, Casa Editrice Ambrosiana.(1998).
-Anichini-Conti-Paoletti, Algebra Lineare e Geometria Analitica Eserciziario, Casa editrice
Pearson.
-Anichini-Conti, Geometria Analitica e Algebra Lineare, Casa editrice Pearson.