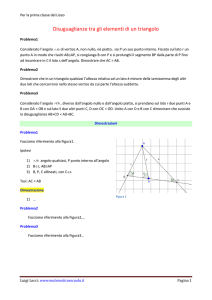
Teorema dell'angolo esterno
Angolo esterno
Un angolo esterno e' qualunque angolo
compreso fra il lato di un triangolo ed il
prolungamento di un'altro lato
quindi possiamo dire che un triangolo ha 6 angoli esterni,
come puoi vedere dalla figura qui a lato
Possiamo inoltre dire che gli angoli esterni sono due a due uguali perche'opposti al
vertice
Enunciato:
In ogni triangolo un angolo esterno e' maggiore di ogni angolo
interno non adiacente
Consideriamo come angolo interno l'angolo BAC^ e come
angolo esterno l'angolo ACD^
ipotesi
tesi
ACD^ esterno
ACD^ > BAC^
Per dimostrare che un angolo e' maggiore di un'altro basta prenderne una parte e
mostrare che la parte e' uguale all'altro angolo, quindi dovremo costruire due triangoli,
uno con l'angolo interno e l'altro con la parte dell'angolo
esterno
ti faccio la costruzione passo-passo.
Considero il punto medio M del
lato AC
Ora considero il
segmento BM e riporto un
segmento uguale sul
prolungamento di BM oltre M,
ottengo il segmento MN
congiungo N con C e considero i
triangoliABM ed MNC
essi hanno
AM = MC per costruzione
BM = MN sempre per costruzione
gli angoli AMB^ = NMC^ perche' opposti al vertice
Per il primo criterio di congruenza i due triangoli sono congruenti, in
particolare BAM^= MCN^ ed essendo MCN^ una parte dell'angoloACD^ si
avra' la tesi