Conversione Elettromeccanica
A.A. 2002/2003
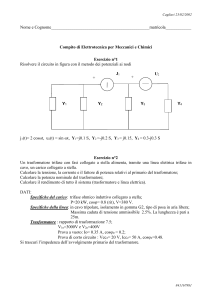
Esercizio 2. CALCOLO DEL RENDIMENTO DI UN TRASFORMATORE
TRIFASE IN DIVERSE CONDIZIONI DI CARICO
Premessa
Nei trasformatori trifase gli avvolgimenti di fase possono essere collegati tra di loro a stella (Y) o a
triangolo (∆).
Se il collegamento è a stella, le tensioni concatenate sono uguali a
3 volte le tensioni di fase
(tensioni ai capi di ciascuna bobina), le correnti di linea sono uguali alle correnti di fase e la
resistenza misurata ai capi di due morsetti è uguale alla serie di due resistenze di fase:
VABY = 3E fY
Ilinea Y = If Y
R ABY = 2R fY
R fY =
R ABY
2
Se il collegamento è a triangolo, le tensioni concatenate sono uguali alle tensioni di fase, le correnti
di linea sono uguali a
3 volte le correnti di fase e la resistenza misurata ai capi di due morsetti è
uguale al parallelo tra una resistenza di fase con una serie di due resistenze di fase:
VAB∆ = E f ∆
Ilinea ∆ = 3If∆
R AB∆ =
R f∆ =
R f∆ i( R f∆ + R f∆ )
R f∆ + ( R f∆ + R f∆ )
=
2R f2∆
3R f∆
=
2
Rf
3 ∆
3
R AB∆
2
Nello studio dei trasformatori trifasi, le potenze, le tensioni e le correnti nominali, così come quelle
misurate nelle prove a vuoto e in corto circuito, si riferiscono rispettivamente a potenze complessive
trifasi, tensioni concatenate e correnti di linea, indipendentemente dai collegamenti degli
avvolgimenti primario e secondario.
Ne consegue che, qualunque siano i collegamenti del primario e del secondario, la potenza
nominale di un trasformatore trifase è data da:
A n = 3V1n I1n = 3V2n I 2n
Esercizio 2 sui trasformatori
Pag. 1 di 4
Conversione Elettromeccanica
A.A. 2002/2003
Infatti, se calcoliamo la potenza nominale di un trasformatore trifase come tre volte la potenza di
ciascuna fase, otteniamo per i due diversi tipi di collegamento:
A n Y = 3E fY IfY = 3
VconcY
Ilinea Y = 3VconcY Ilinea Y
3
A n ∆ = 3E f ∆ If∆ = 3Vconc∆
Ilinea ∆
3
= 3Vconc∆ Ilinea ∆
Per ricondursi allo studio di un circuito equivalente semplificato analogo a quello del trasformatore
monofase, occorre prima di tutto considerare un trasformatore trifase equivalente stella-stella,
qualsiasi siano i collegamenti del trasformatore trifase di partenza.
Nel caso in cui un avvolgimento sia collegato a triangolo, occorre applicare la trasformazione
triangolo-stella:
R fY =
R f∆
3
In condizioni di carico simmetrico ed equilibrato, lo studio del trasformatore trifase equivalente a
stella viene ricondotto a quello del circuito equivalente semplificato di una singola fase.
Esercizio 2
Si consideri un trasformatore trifase di cui sono noti i seguenti dati:
−
potenza apparente nominale
An = 200 kVA
−
tensione primaria nominale
V1n = 20 kV
−
tensione secondaria nominale
V2n = 400 V
−
perdite a vuoto
P0 = 1,25 kW
−
collegamento e gruppo
Dyn11
−
resistenza misurata ai capi di 2 morsetti primari
RAB = 10 Ω
−
resistenza misurata ai capi di 2 morsetti secondari
Rab = 28 mΩ
−
fattore di potenza del carico
cosϕcarico = 0,9
Si determinino:
a) le perdite di corto circuito Pccn;
b) il fattore di carico xηmax per il quale il rendimento risulta massimo, essendo il trasformatore
connesso ad un carico con tensione V2 = V2n e cosϕcarico = 0,9;
c)
i rendimenti per diversi valori del fattore di carico: x = 0,2; 0,4; 0,6; 0,8; 1, con V2 = V2n e
cosϕcarico = 0,9.
Esercizio 2 sui trasformatori
Pag. 2 di 4
Conversione Elettromeccanica
A.A. 2002/2003
Soluzione dell’Esercizio 2
a) Calcoliamo la resistenza di una fase del primario e di una fase del secondario.
Il primario è collegato a triangolo, quindi:
R AB∆ =
2
Rf1
3 ∆
⇒
R f 1∆ =
3
3
R AB∆ = ⋅10 = 15 Ω
2
2
Il secondario è collegato a stella, quindi:
R abY = 2R f 2Y
⇒
R f 2Y =
R abY
2
=
28
= 14 mΩ = 0, 014 Ω
2
Dobbiamo ricondurci al circuito equivalente di una fase, facendo riferimento a un trasformatore
trifase equivalente con collegamento a stella sia al primario che al secondario.
Il circuito equivalente di una fase a cui faremo riferimento è analogo a quello utilizzato per lo
studio del trasformatore monofase. La tensione ai capi del primario è una tensione di fase.
Le impedenze di corto circuito Z1 e Z’2 possono essere suddivise nelle corrispondenti resistenze
e reattanze:
Le resistenze R1 e R’2 sono quelle di una fase del trasformatore trifase equivalente stella-stella.
Poiché il primario è collegato a triangolo, la resistenza corrispondente a una fase
dell’avvolgimento trifase equivalente collegato a stella è: R1 =
R f 1∆
3
=
15
= 5Ω
3
Il secondario è invece collegato a stella, perciò: R 2 = R f 2Y = 0, 014 Ω
Esercizio 2 sui trasformatori
Pag. 3 di 4
Conversione Elettromeccanica
A.A. 2002/2003
2
20000
La resistenza del secondario riportata a primario è: R '2 = k R 2 =
⋅ 0, 014 = 35 Ω
400
2
La resistenza complessiva riportata a primario è: R1cc = R1 + R '2 = 5 + 35 = 40 Ω
Le perdite in corto circuito, tenendo conto che il circuito equivalente considerato è relativo a
2
una sola fase, sono: Pcc = 3R1cc I1n
Calcoliamo la corrente nominale primaria: I1n =
An
200000
10
=
=
A
3V1n
3 ⋅ 20000
3
2
⇒
b)
10
Pcc = 3R I = 3 ⋅ 40 ⋅
= 4000 W = 4 kW
3
2
1cc 1n
x ηmax =
ηmax =
P0
1, 25
=
≅ 0,559 = 55,9%
Pcc
4
1
1
1
=
=
≅ 0,9758 = 97,58%
2 P0 Pcc
2 P0 Pcc
2 1, 25 ⋅ 4
1+
1+
1+
200 ⋅ 0,9
Pn
A n cos ϕcc
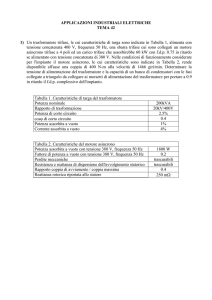
c) Per il calcolo del rendimento per diversi valori del fattore di carico si utilizza la formula:
η=
xPn
xPn + P0 + x 2 Pcc
con:
Pn = A n cos ϕcarico = 200 ⋅ 0,9 = 180 kW
Sostituendo i diversi valori del fattore di carico, otteniamo:
Esercizio 2 sui trasformatori
Fattore di carico x
Rendimento η
1
97,17%
0,8
97,42%
0,6
97,57%
0,4
97,44%
0,2
96,23%
Pag. 4 di 4