Esercizio svolto 1
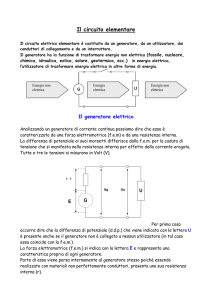
Dati:
R1 = 4
R2 = 3
R3 = 1
I G = 4A
=2
Determinare la corrente I e le potenze rispettivamente erogate dal
generatore Ig e dal generatore αI.
Per trovare la grandezza pilota uso la sovrapposizione degli effetti
1. Considero solo il generatore di corrente Ig, aprendo αI:
R1
I'
R2
3 3
I ' = IG
=4 =
R2
R1 R2R 3
8 2
R3
Ig
2. Considero solo il generatore di corrente dipendente αI:
R1
I''
R3
4
I'' = −I
=− I
R2
R1R2 R3
8
αI
R3
(metto il meno perché αI immette corrente nel verso opposto)
Per trovare la corrente I, effettuo la somma algebrica di I' e I'':
3
4
I = I' I ' ' = − I
2 8
4
3
3
3
I I =
I=
I =1
8
2
2
2
Per trovare le potenze erogate dai singoli generatori devo trovare le correnti su R2 ed R3:
Sapendo che αI = 4A e Ig = 4A
R1
1
2 I
I
IR2
R3
Scrivo le LKC:
α
R2
Nodo1 : − I R I G − I = 0
I
R3
Ig
Nodo 2: I I − I R = 0
Nodo3 : I R − I G − I I R = 0
{
3
Risoluzione della prima equazione:
−I R 4 − 1 = 0 I R = 3
2
2
2
3
2
3
Risoluzione della seconda equazione:
1 4 − IR =0 I R =5
3
3
Verifico i risultati ottenuti con la terza equazione (che è ridondante):
3 − 4 − 4 5 = 0 0 = 0 verificata
Calcolo la potenza erogata da Ig:
La tensione tra il nodo 1 e il nodo 3 si ottiene mediante: R2 I R = 3⋅ 3 = 9V
La potenza erogata si ottiene infine mediante: 9V⋅ I G = 9V ⋅ 4A = 36W
2
Calcolo la potenza erogata da αI:
La tensione tra il nodo 2 e il nodo 3 si ottiene mediante: R3 I R = 1⋅5 = 5V
La potenza erogata si ottiene infine mediante: 5V⋅ I = 5V⋅4A = 20W
3
Aleksandar Gotev – Elettrotecnica – Esercizi svolti con generatori dipendenti
1
Esercizio svolto 2
Dati:
R1 = 5
I3
R2 = 1
R3 = 2
I G = 2A
= 3
Determinare la corrente I e le potenze generate da Ig e αI.
Per trovare la corrente I ed I3 (necessaria per il calcolo della potenza),
uso la sovrapposizione degli effetti.
1. Considero solo il generatore di corrente Ig, aprendo αI:
R 2 R3
12
6
=− 2
=−
R 1 R 2 R3
512
8
R1
5 10
I 3' = I G
=2 =
R 1 R2 R 3
8
8
I ' = − IG
I3
2. Considero solo il generatore di corrente αI, aprendo Ig:
R3
2
6
= 3I = I
R1 R2 R3 8
8
R1 R2
6
18
I 3' ' = − I
= − 3I = −
I
R1 R 2 R 3
8
8
I ' ' = I
I3
3. Trovo I ed I3:
6 6
I
8 8
10 18
I 3 = I 3' I 3' ' =
−
I
8
8
I = I' I ' ' =−
6
6
I =−
8
8
10 54
I3 =
8
8
I−
2
6
I =−
8
8
I = − 3A
I 3 = 8A
Calcolo la potenza erogata da Ig:
P I = R1 ⋅ I ⋅ I G = 5⋅3 ⋅2 = 30W
G
Calcolo la potenza erogata da αI:
P I = R3 ⋅ I 3 ⋅ I = 2⋅ 8⋅3⋅ 3 = 144W
Aleksandar Gotev – Elettrotecnica – Esercizi svolti con generatori dipendenti
2
Esercizio svolto 3
Dati:
R1 = 1
R2 = 3
R3 = 2
I G = 3A
g = 0,5 S
*1 [S] (Siemens) = 1A/V (Conduttanza elettrica)
Determinare la tensione V2 e le potenze erogate da IG e gV2.
Per trovare V2 e V1 (necessaria per calcolare la potenza), uso la sovrapposizione degli effetti.
1. Considero solo il generatore IG, aprendo gV2:
R1 R3
3 9 3
=3 = =
R1 R2 R3
6
6 2
R2
3 9
3
I 1' = IG
=3 = =
R1 R2R3
6 6
2
I 2' = I G
I1
I2
2. Considero solo il generatore gV2, aprendo IG:
g V 2 = g ⋅ R2 ⋅ − I 2 = 0,5⋅ 3⋅ − I 2 = −1,5 I 2
Metto il meno davanti a I2 perché il resistore è un utilizzatore e
non può avere i versi concordi di tensione e corrente.
I1
I2
R1
1,5
0,5
=
I =
I
R1 R2R 3
6 2
2 2
R2R 3
7,5
2,5
I 1 ' ' = 1,5 I 2
=
I =
I
R1R 2R3
6 2
2 2
I 2 ' ' = 1,5 I 2
3. Trovo I1, I2, V1 e V2:
3 0,5
I 2 = I2' I2 ' ' =
I
2
2 2
I2−
0,5
3
I2=
2
2
I2=
3
= 2A
1,5
V 2 = − I 2 ⋅ R2 = − 2⋅ 3 = −6V
Metto il meno davanti a I2 perché il resistore è un utilizzatore e non può avere i versi concordi di tensione e corrente.
I 1 = I 1' I 1 ' ' =
3
2,5
2
2
2
I1 =
8
= 4A
2
V 1 = I 1 ⋅ R1 = 4 ⋅1 = 4V
Calcolo la potenza erogata da Ig:
P I = I G ⋅V 2 = 3⋅ 6 = 18W
G
Calcolo la potenza erogata da gV2:
P g V = V 1 ⋅ g V 2 = 4⋅ 0,5⋅6 = 12W
2
Aleksandar Gotev – Elettrotecnica – Esercizi svolti con generatori dipendenti
3
Esercizio svolto 4
Dati:
R1 = 4
R2 = 1
R3 = 2
E 1 = 30V
E 2 = 12V
=3
Determinare la tensione V2 e le singole potenze erogate da ogni
generatore.
Uso la sovrapposizione degli effetti.
1. Considero solo il generatore μV2, cortocircuitando E1 ed E2:
V AB =
VAB
I 3' =
I 2' =
I 1' =
V 2
R3
3 4
6
= ⋅ V2 = V2
1
1
1
2 7
7
R1
R2
R3
V AB − V 2
15 1
15
= − ⋅ V 2 =− V 2
R3
7 2
14
V AB 6
= V2
R2
7
V AB 6 1
3
= ⋅ V2=
V
R1
7 4
14 2
2. Considero i generatori E1 ed E2 cortocircuitando μV2 :
E1 E 2
30
−
−
− 12
R1
R2
4
78
=
=−
1
1
1
7
7
R1
R2
R3
4
V AB
78 1
39
=− ⋅ = −
R3
7 2
7
E 2 V AB
6
=
R2
7
E 1 V AB 132 1 33
=
⋅ =
R1
7 4
7
−
V AB =
VAB
I 3' ' =
I 2' ' =
I 1' ' =
3. Trovo le correnti I1,I2 ed I3:
V 2 = R2 ⋅ I 2 = I 2
6
6
6
6
I 2 = I 2 ' I 2' ' = I 2
I 2− I 2 =
I2 = 6
7
7
7
7
3
33
42
I 1 = I 1' I 1' ' =
6
I1 =
=6
14
7
7
15
39
84
I 3 = I 3' I 3' ' = −
6−
I3 = −
= − 12
14
7
7
4. Calcolo le potenze erogate dai generatori:
P V = V 2 ⋅ I 3 = 216W
P E = E 1 ⋅ I = 30 ⋅6 = 180W
2
1
P E = E 2 ⋅ I 2 = 72W
2
Aleksandar Gotev – Elettrotecnica – Esercizi svolti con generatori dipendenti
4
Esercizio svolto 5
Dati:
R1 = 4
R4 = 6
g = 0,5 S
R2 = 2
E1 = 12V
R3 = 4
E 2 = 12V
1[S ]Siemens = 1 V / A
Determinare le correnti dei resistori
Come prima cosa si nota che la tensione ai capi di R4 è imposta da E2, per cui si può calcolare subito
la corrente I4:
E
12
I4= 2 =
= 2A
R4
6
La resistenza R4 non influisce sul resto del circuito. Si nota che i rami del circuito sono posti tutti i
parallelo, per cui è possibile calcolare la tensione VAB supponendo noto il valore del generatore
dipendente:
E1
E
− gV 3 2
R
R3
3 −2I3 3
V AB = 1
=
= 6−2 I 3
1
1
1
1
R1
R2
R3
Trovo la grandezza pilota:
V − E2
− 6− 2I3
3 1
I 3 = AB
=
= − − I3
R3
4
2 2
3
3
I3 = −
2
2
I 3 = − 1A
A questo punto posso trovare il valore numerico di VAB:
V AB = 6 − 2 I 3 = 6 2 = 8V
Trovo le altre correnti:
E 1 − V AB 12 − 8
I1=
=
= 1A
R1
4
V
8
I 2 = AB = = 4A
R2
2
Aleksandar Gotev – Elettrotecnica – Esercizi svolti con generatori dipendenti
5
Esercizio svolto 6
Dati:
R1 = 4
E 1 = 8V
R2 = 10
R3 = 4
E 2 = 8V
= 3
Determinare le correnti nei resistori
Uso la sovrapposizione degli effetti.
1. Considero solo il generatore E1, cortocircuitando gli altri 2:
Noto che cortocircuitando gli altri due generatori, la resistenza R2 è collegata in parallelo ad un
corto circuito, per cui non la considero. Graficamente ho questa situazione:
Posso procedere a calcolare le due correnti:
E1
I 1' = −
= − 2A
R1
E
I 3 ' = 1 = 2A
R3
2. Considero solo il generatore αV1, cortocircuitando gli altri 2:
Noto che i punti A, B e C sono equipotenziali, dato che sono collegati
tramite dei cortocircuiti, quindi posso ridisegnare il circuito per
renderlo più facilmente interpretabile:
αV1
I 1' ' =
R1 I1
3V1 3
= V1
R1
4
R2 I2
I 2' ' =
Nota:
In R3 non scorre corrente
perché è ai capi di un
corto circuito
3V1
3
=
V
R2
10 1
3. Considero solo il generatore E2, cortocircuitando gli altri 2:
Noto che cortocircuitando gli altri due generatori, la resistenza R1 è collegata in parallelo ad un
corto circuito, per cui non la considero. Graficamente ho questa situazione:
Posso procedere a calcolare le due correnti:
E
E
8
I 2' ' ' = 2 =
A
I 3 ' ' ' = 2 = 2A
R 2 10
R3
4. Trovo tutte le correnti come somma algebrica dei contributi dei generatori:
3
I 1 = − 2 R1 I 1
I1 − 3 I1 = − 2
I 1 = 1A
4
12
8
I2=
= 2A
10 10
I 3 = 2 2 = 4A
Aleksandar Gotev – Elettrotecnica – Esercizi svolti con generatori dipendenti
6