CAPITOLO 6 - Il Mosfet Rev1

CAPITOLO VI
Il MOSFET
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-1
IV.1 Introduzione
Attualmente la tecnologia più utilizzata per la realizzazione di circuiti integrati fa uso del transistor
MOSFET. Il transistor MOSFET (Metal-Oxide-Semiconductor Field Effect Transistor) è un
dispositivo unipolare, al contrario del BJT.
Realizzato per la prima volta nel 1960 ha visto un enorme successo grazie all’avvento della tecnologia
CMOS (complementary MOS) che consente di realizzare nello stesso processo e sullo stesso substrato
transistor MOS complementari in modo più semplice e meno costoso rispetto alla tecnologia bipolare.
Presenta un consumo di potenza statica praticamente nullo ed è una tecnologia molto diffusa nei
circuiti digitali ma è anche usata in sistemi analogici. I circuiti digitali guidano lo sviluppo
tecnologico poiché permettono di realizzare memorie. Inoltre la CMOS è una tecnologia poco costosa
(rispetto alla Bipolare e BiCMOS).
Il MOSFET si basa sulla polarizzazione di una doppia giunzione tra tre materiali: metallo, ossido
(isolante) e semiconduttore. Il silicio è divenuto negli scorsi decenni il materiale principe della
microelettronica anche grazie alla possibilità di realizzare attraverso opportuni processi tecnologici sia
il conduttore (silicio policristallino o polisilicio altamente drogato), che l’ossido (ossido di silicio) che
ovviamente il semiconduttore (silicio monocristallino).
Se si prendono separatamente questi tre materiali essi hanno le proprie tipiche caratteristiche fisiche:
funzione di lavoro e affinità elettronica. La funzione di lavoro ci dà l’informazione su quanta energia
sia mediamente necessaria per strappare un elettrone dal materiale.
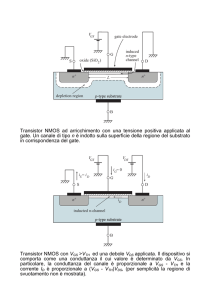
Per studiare il sistema MOS (Metallo-Ossido-Semiconduttore) consideriamo l’alluminio, il SiO2 ed il
silicio drogato di tipo p (vedi figura)
Si può osservare che la funzione di lavoro qφS del semiconduttore è maggiore di quella del metallo.
Quando si uniscono i tre materiali, si forma una doppia giunzione come in figura e si ha un
trasferimento di elettroni dal metallo che ha funzione di lavoro qφM < qφS . Il trasferimento però non
può avvenire attraverso lo strato di ossido che costituisce un’elevatissima barriera di energia da
superare per gli elettroni, ma attraverso un allontanamento di elettroni dall’interfaccia metallo-ossido (
cioè un addensamento di carica positiva) e un addensamento di elettroni all’interfaccia
semiconduttore-ossido (addensamento di carica negativa).
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-2
E’ dunque come se avessi un addensamento di carica ai capi del condensatore con la formazione di
una differenza di potenziale ΔV ai capi del SiO2.
Si ha la formazione di una regione di carica spaziale (o svuotamento) nel semiconduttore ed il sistema
equivale ad un condensatore costituito dalle due armature (carica addensata ai capi dell’ossido) ed un
dielettrico (il SiO2).
In prima approssimazione il potenziale a cui è caricato il condensatore è pari alla differenza delle due
funzioni di lavoro moltiplicata per q (carica dell’elettrone):
ΔV = φS − φM
Polarizzazione del sistema MOS con un potenziale negativo al metallo
Se applico una tensione esterna ovviamente modifico la carica immagazzinata nel condensatore.
Applicando un potenziale leggermente negativo al metallo riduco la carica positiva addensata
all’interfaccia M-O ed il piegamento delle bande viene ridotto. Questa regione si dice di svuotamento
ed in questo caso ho una leggera carica positiva al metallo (per effetto dell’allontanamento di
elettroni) e una leggera carica negativa all’interfaccia ossido-semiconduttore per effetto
dell’allontanamento di lacune che porta alla formazione di ioni negativi positivi (quindi la carica
negativa non è una carica mobile).
Aumentando il potenziale negativo, la carica positiva è azzerata si ha la condizione di banda piatta e
la tensione applicata si dice tensione di banda piatta VFB (flat band voltage).
Tale tensione compensa la differenza tra le due funzioni di lavoro e dipende oltre che da altri
parametri da:
• Densità di drogante (funzione di lavoro nel semiconduttore)
• Tipo di metallo (funzione di lavoro nel metallo)
Definisco
V 'FB = φM − φS = φMS
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-3
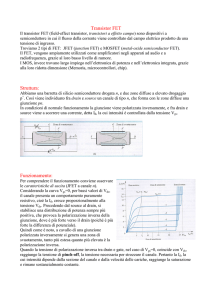
Quando la tensione negativa applicata è, in modulo, maggiore di V 'FB (con il semiconduttore a massa)
inverto la carica immagazzinata alle interfacce (negativa in M-O e positiva in S-O) ed il piegamento
delle bande si inverte. Si può osservare che adesso il livello di Fermi all’interfaccia semiconduttoreossido è ancora più vicino al bordo della banda di valenza del silicio drogato p, indice che vi è un
ulteriore accumulo di carica positiva in prossimità dell’ossido rispetto alla popolazione di lacune nella
regione quasi-neutra pari a N A .
Questa è la condizione di accumulo superficiale.
Polarizzazione del sistema MOS con un potenziale positivo al metallo
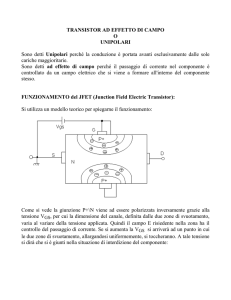
Se invece applico al metallo una tensione positiva, svuoto ulteriormente il silicio in prossimità
dell’ossido.
Con il potenziale positivo applicato al metallo si ha generazione di coppie elettrone-lacuna nel silicio.
Le lacune vanno verso la regione quasi-neutra (bulk) del silicio e gli elettroni si addensano
all’interfaccia ossido-silicio, dove sono bloccate a causa della presenza della barriera di ossido.
Questo fenomeno può portare alla creazione localizzata di portatori liberi alla superficie del silicio
(interfaccia con l’ossido) in equilibrio con quelli nel volume del silicio. Infatti il livello di Fermi è
costante e la concentrazione di elettroni segue la statistica di Fermi-Dirac.
Aumentando la tensione positiva il livello di Fermi E F attraversa il livello intrinseco Ei e la
concentrazione di elettroni aumenta ancora alla superficie del silicio.
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-4
Si crea uno strato di inversione, cioè un materiale drogato p, ha nella regione di superficie in
prossimità dell’ossido un’inversione di popolazione con un forte eccesso di elettroni. Tale regione
diventa dunque equivalente ad un materiale drogato n.
Si è dunque creata una giunzione p-n tra la superficie del silicio (n) e la regione p lontana dalla
superficie.
• Se vale Ei ≥ E f S , cioè se il livello di Fermi nella regione di volume del semiconduttore è
•
inferiore al livello di Fermi intrinseco all’interfaccia ossido-silicio allora si ha la condizione di
debole inversione.
Se ( EC − E fS ) all 'interf .O − Si < ( E fS − EV ) nel Sibulk , cioè se la concentrazione di elettroni
all’interfaccia Si-O risulta maggiore di quella di lacune nel volume si ha la condizione di forte
inversione.
Quindi l’applicazione di una tensione positiva porta a :
• Allontanamento di lacune dalla regione di svuotamento
• Richiamo di elettroni nello strato di inversione.
In regime di forte inversione l’estensione W della regione di carica spaziale si mantiene in prima
approssimazione costante con la tensione applicata.
Campo elettrico e potenziale all’interfaccia e lungo la sezione del dispositivo sono illustrati in figura.
Il campo elettrico è discontinuo a causa della differente costante dielettrica dei materiali (ossido e
semiconduttore) e ovviamente nullo nel metallo.
Il potenziale VGB applicato tra metallo (gate - G) e substrato (bulk – B) si distribuisce tra l’ossido( Vox ),
dove la caduta di potenziale è lineare (quindi il campo elettrico è costante) e la regione di carica
spaziale del semiconduttore ( Vs ).
La condizione di banda piatta è quella in cui il potenziale è costante (neutralità di carica) per cui il
potenziale applicato risulta in realtà VGB − VFB
Quindi vale VGB − VFB = Vox + Vs
Se definisco QG la carica per unità d’area indotta nel metallo (positiva) e QB la carica (negativa) per
unità di area indotta nel substrato si ha
QG = −QB = CoxVox
quindi posso scrivere
Q
Q
VGB − VFB = Vox + Vs = Vs + G = Vs − B
Cox
Cox
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-5
Ricapitolando, la superficie del silicio può essere:
1. altamente conduttiva e connessa elettricamente al volume quando è accumulata ( VGB < 0 ,
VGB < VFB )
2. altamente isolante quando è svuotata ( VGB > VFB )
3. altamente conduttiva e non connessa elettricamente al volume quando è in inversione
(VGB  0 )
Capacità del sistema MOS
Se VGB < 0 il sistema MOS visto in precedenza con substrato drogato p. si trova in condizione di
accumulo di cariche positive all’interfaccia ossido-silicio. Se sovrappongo una tensione alternata di
piccola ampiezza, la capacità totale è prossima a quella dell’ossido, infatti la carica che si accumula
per effetto del segnale è piccola rispetto al condensatore costituito dalle due armature (cariche
accumulate alle interfacce M-O e O-S) e dallo spessore dell’ossido xoss .
In accumulazione la capacità MOS per unità di area vale:
C 'oss =
ε oss
xoss
Se VG > VFB dalla condizione di banda piatta comincia a crearsi una regione svuotata ed ho la serie di
due capacità:
• Capacità dell’ossido
• Capacità della regione di carica spaziale
Quindi la capacità diviene:
1
C'=
1
+W
C 'oss
ε silicio
Quindi la capacità diminuisce all’aumentare di W (regione di carica spaziale).
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-6
Proprietà elettroniche del sistema MOS
Consideriamo un’interfaccia in equilibrio con il substrato.
Vediamo le proprietà elettroniche in funzione delle diverse regioni di funzionamento sapendo che il
potenziale applicato nel sistema MOS si distribuisce secondo la relazione
Q
Q
VGB − VFB = Vox + φs = φs + G = φs − B
Cox
Cox
Regione di accumulazione
Abbiamo visto che per VGB < VFB si ha accumulazione di lacune in prossimità dell’interfaccia O-S.
In questa condizione QG è negativa.
La carica si addensa tutta in prossimità dell’interfaccia, la regione di carica spaziale è ridottissima e si
può considerare nulla, e quindi il campo elettrico ed il potenziale nel semiconduttore nulli
Q
Q
VGB − VFB = Vox = G = − B
Cox
Cox
Regione di svuotamento
Se la tensione VGB è di poco maggiore della tensione di banda piatta ( VGB > VFB ma di poco) la carica
QG è positiva e QB negativa.
Si ha una regione svuotata costituita da ioni negativi, causata dalla repulsione di lacune dalla
superficie del substrato.
Si assume che nella regione svuotata:
• Tutti gli atomi di drogante siano ionizzati
• La regione si estende xd
• Sia priva di portatori liberi ( p = n = 0 )
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-7
Sotto queste ipotesi la concentrazione o densità di carica può essere espressa come:
ρ s ( x) = −qN AB per 0 ≤ x ≤ xd
La carica QB in queste condizioni è pari alla carica della regione svuotata che viene indicata con Qd .
xd
QB = Qd = ∫ ρs ( x)dx = −qN AB xd
0
Il campo elettrico si ricava dall’equazione di Poisson:
qN AB
ρ ( x)
ρ ( x)
d
( x) = s
⇒
( x) = ∫ s
dx = −
x + C1
dx
εs
εs
εs
ε
ε
per
0 ≤ x ≤ xd
La costante C1 si ricava ponendo l’annullamento del campo elettrico in xd (fine della regione di
carica spaziale e inizio di quella quasi-neutra) come condizione al contorno
qN AB xd
qN AB xd
−
+ C1 = 0
⇒
C1 =
εs
εs
ε ( x) = − qNε
AB
( x − xd )
per
0 ≤ x ≤ xd
s
Integrando una seconda volta ottengo il potenziale:
V ( x) = − ∫ ε ( x)dx =
qN AB
εs
( x − xd ) 2 + C2
per
0 ≤ x ≤ xd
La costante C2 si ricava ponendo l’annullamento del potenziale in xd (in realtà in xd il potenziale si
trova a un potenziale −φ p che considero quale potenziale di riferimento) come condizione al contorno
da cui
qN AB
V ( x) =
( x − xd ) 2
per
0 ≤ x ≤ xd
2ε s
Il potenziale di superficie quindi è dato da
qN AB 2
φs = V (0) =
xd
2ε s
da cui si ricava anche xd in funzione di φs , xd =
2ε sφs
che sostituito nella
qN AB
xd
QB = Qd = ∫ ρs ( x)dx = −qN AB xd permette di ricavare la carica della regione svuotata in funzione del
0
potenziale di superficie Qd = − 2qε s N AB φs ;
quindi posso calcolare la carica QB , in funzione del potenziale applicato VGB , sostituendo Qd nella
Q
Q
espressione VGB − VFB = φs − B = φs − d
Cox
Cox
Regione di inversione
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-8
Aumentando ulteriormente la tensione VGB rispetto a VFB si è visto che aumenta la carica di superficie
QB e si può creare un canale di inversione attraverso l’avvicinamento di una carica di elettroni liberi
Qc che in prima approssimazione si può considerare concentrata in una regione di spazio molto
ristretta in prossimità dell’interfaccia O-S.
Adesso QB = Qd + Qc
In prima approssimazione Qc è proporzionale alla carica di portatori liberi alla superficie del silicio
n(0) che si può calcolare dall’equazione di Boltzmann per gli elettroni, in cui la differenza di
concentrazione tra due punti è esponenzialmente legata alla differenza di potenziale tra i due punti
stessi.
n(0) = n( xd )e
q (V (0) −V ( xd ))
kT
inoltre sappiamo che per la legge di azione di massa n( xd ) =
ni 2
N AB
e
V (0) − V ( xd ) = φs
quindi
qφ
ni 2 kTs
n(0) =
e
N AB
Quindi la carica all’interfaccia dipende esponenzialmente dal potenziale di superficie.
Analizziamo in dettaglio la precedente relazione per capire come Qc influisca su QB .
Se il potenziale di superficie diviene abbastanza grande e pari a φs =
kT N A
allora
ln
q
ni
la concentrazione n(0) diviene pari alla concentrazione intrinseca nel silicio n(0) = ni . Ricordando
kT N A
che
ln
= φF (potenziale di Fermi) si ha che la caduta di potenziale ai capi della regione
q
ni
svuotata è pari al potenziale di fermi φF = φs .
Quindi se il potenziale di superficie è maggiore del potenziale di Fermi φs > φF allora n(0) > ni , cioè
la concentrazione di elettroni liberi è maggiore della concentrazione intrinseca ed il semiconduttore
può essere considerato di tipo n ed entro nella regione di inversione.
Qc non è però ancora confrontabile con Qd , e Qc si può ancora ritenere nullo o trascurabile.
La carica di canale Qc (proporzionale a n(0) ) diviene almeno pari alla carica della regione svuotata
Qd (proporzionale a N AB ) quando ns = n(0) = N AB , che sostituita nella n(0) =
qφ
ni 2 kTs
e porta a
N AB
qφs
N AB 2 = ni 2e kT
2
kT N AB
kT N A
φs =
ln 2 = 2 ⋅ ln B = 2φF
q
ni
q
ni
Ricapitolando:
- Per φF < φs < 2φF ho la condizione di debole inversione
- Per φs > 2φF ho la condizione di forte inversione.
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-9
In condizione di forte inversione, per il legame esponenziale tra n(0) e φs , piccole variazioni di φs
portano a grosse variazioni di n(0) e di fatto il valore di φs non varia molto rispetto a 2φF e si può
considerare
φs ≅ 2φF
Il valore della massima estensione della regione svuotata xd = xd MAX si può ricavare sostituendo
φs = 2φF in φs = V (0) =
xdMAX =
qN AB
2ε s
xd 2 e si ottiene
4ε sφF
qN AB
che sostituita nell’espressione QB = Qd =
xd
∫ ρ ( x)dx = −qN
s
AB
xd permette di ottenere il massimo valore
0
della carica della regione svuotata
QdMAX = − 4qε s N AB φF
Quindi in regione di inversione si ha che
2qε s N AB φs Qc
Q
Q
QB
= φs − d − c = φs +
−
Cox
Cox Cox
Cox
Cox
Quindi un aumento della tensione applicata VGB comporta un aumento della carica di canale
(avvicinamento di elettroni) e di quella della regione svuotata (allontanamento di lacune).
VGB − VFB = φs −
Tale espressione si può riscrivere in ipotesi di debole inversione e forte inversione.
In debole inversione la carica Qc si può ritenere trascurabile:
2qε s N AB φs
Q
QB
≈ φs − d = φs +
Cox
Cox
Cox
In forte inversione il potenziale di superficie φs ≅ 2φF e
VGB − VFB = φs −
4qε s N AB φF Qc
Qd
Q
QB
= 2φF − MAX − c = 2φF +
−
Cox
Cox Cox
Cox
Cox
Solo in quest’ultima condizione si assume presente la carica Qc e risulterà dunque presente un canale
elettronico sotto il gate.
VGB − VFB ≈ 2φF −
Tensione di soglia
La tensione di soglia VTH 0 è quella applicata tra gate e substrato VGB perché si verifichi la formazione
del canale, cioè la creazione di carica Qc .
Come in precedenza si assume nulla la carica Qc in debole inversione, e si considera il canale formato
solo in forte inversione dove il potenziale superficiale si assume pari a 2φF . Si è visto che in forte
inversione
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-10
4qε s N AB φF
Qc
Q
= 2φF + γ 2φF − c
Cox
Cox
Cox
dove il coefficiente γ è chiamato coefficiente di effetto substrato è
VGB − VFB = 2φF +
γ=
−
2qε s N AB
Cox
Risolvendo la precedente espressione per Qc si ottiene
−Qc = Cox ⎡⎣VGB − (VFB + 2φF + γ 2φF ) ⎤⎦
e quindi il canale si forma per VGB > (VFB + 2φF + γ 2φF )
Quindi la tensione di soglia è
VTH0 = VFB + 2φF + γ 2φF
Quindi nota la tensione di soglia, la carica nel canale può essere ottenuta dalla relazione
−Qc = Cox (VGB − VTH 0 )
Applicazione di una polarizzazione alle regioni diffuse
Si è visto che polarizzando il sistema MOS positivamente posso raggiungere la condizione di
inversione con la formazione di una giunzione p-n tra la superficie ed il volume del silicio.
Se applico Vc ad una delle regioni diffuse provoco un aumento della regione svuotata sotto di essa e
quindi della carica Qd (come in un diodo polarizzato inversamente). Poiché la carica QB si ripartisce
tra carica di canale Qc e carica Qd , l’aumento di quest’ultimo comporta una diminuzione di Qc .
Quindi applicando Vc > 0 devo applicare una tensione di gate maggiore per per mantenere costante
Qc .
Applicando Vc il potenziale di superficie in forte inversione diviene (2φF + Vc ) e
xdMAX =
2ε s (2φF + Vc )
con Qd = − 2qε s N AB (2φF + Vc )
qN AB
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-11
La caduta di potenziale sul sistema MOS diviene:
2qε s N AB φs Qc
2qε s N AB (2φF + Vc ) Qc
Q
Q
Q
VGB − VFB = φs − B = φs − d − c = φs +
−
= (2φF + Vc ) +
−
Cox
Cox Cox
Cox
Cox
Cox
Cox
Successivamente all’applicazione del potenziale Vc le due regioni si possono scrivere:
- Per φF < φs − Vc < 2φF ho la condizione di debole inversione
- Per φs − Vc > 2φF ho la condizione di forte inversione.
qφs
La carica del canale diviene quindi non più proporzionale a e kT ma a e
q (φs −Vc )
n2
n(0) = i e kT
N AB
q (φs −Vc )
kT
:
e per la legge di azione di massa
q (φs −Vc )
−
ni2
p(0) =
= N AB e kT
n(0)
Se esiste il modo di accedere alla superficie del silicio è possibile polarizzare questa giunzione.
La figura mostra che è possibile polarizzare la giunzione con una tensione (VC − VB ) opportuna.
Per non avere correnti circolanti tra l’interfaccia ed il volume (correnti parassite e dannose per il
dispositivo) la giunzione è polarizzata inversamente.
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-12
L’applicazione di una tensione di source e di una tensione di drain fanno sì che si determini un
potenziale di canale Vc ( y) che è funzione della posizione tra 0 e L lungo y al di sotto del gate tra i due
elettrodi tra cui scorre la corrente source (S) e drain (D):
Vc (0) = VS
Vc ( L) = VD
Lungo la direzione x (trasversale alla giunzione) il potenziale è imposto dal gate con VG che si
ripartisce tra ossido e semiconduttore (quest’ultima caduta di potenziale è rappresentata dal potenziale
di superficie).
Il potenziale di superficie nell’ipotesi di esistenza del canale (forte inversione) è φs ≅ 2φF , quindi
come appena visto, applicando un potenziale alle regioni diffuse di source e drain (applicazione
contemporanea delle tensioni VG , VS e VD ) si ottiene un potenziale di superficie:
φs ( y) = 2φF + Vc ( y)
Quindi lungo il canale (direzione y) variano φs , Qc e Qd .
Q
Dunque la precedente relazione VGB − VFB = φs − B si riscrive
Cox
2qε s N AB φs ( y) Qc ( y)
Qd ( y) Qc ( y)
−
= φs ( y) −
−
Cox
Cox
Cox
Cox
che in forte inversione ( φs ( y) = 2φF + Vc ( y) ) diventa
Q ( y)
VGB − VFB = 2φF + Vc ( y ) + γ 2φF + Vc ( y ) − c
Cox
E’ evidente che muovendosi dal source al drain la carica Qd aumenta mentra quella Qc diminuisce.
Per semplificare la trattazione di solito si considera costante il valore di Qd ( y ) , considerandone il
valore al source.
VGB − VFB = φs ( y) −
Allora il termine
Qd ( y )
si approssima a
Cox
Qd ( y )
= −γ 2φF + Vc ( y ) ≈ −γ 2φF + VS
Cox
con questa approssimazione la carica di canale si può ricavare dalla relazione
Q ( y)
VGB − VFB = 2φF + Vc ( y ) + γ 2φF + Vc ( y ) − c
Cox
e si ottiene
Qc = −Cox ⎡⎣VGB − (VFB + 2φF + γ 2φF + VS ) − Vc ( y ) ⎤⎦
e la tensione di soglia del transistor MOS VTH si può scrivere
VTH = VFB + 2φF + γ 2φF + VS
e la forma semplificata della carica di canale diviene
Qc = −Cox [VGB − VTH − Vc ( y)]
La carica è nulla e non positiva al di sotto della tensione di soglia.
Ricapitolando
⎧−
⎪ Cox [VGB − VTH − Vc ( y)]
Qc ( y) = ⎨
⎪⎩0
per
VG − Vc ( y ) > VTH
per
VG − Vc ( y) < VTH
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-13
La relazione per VTH si riduce a quella per VTH 0 ( VTH0 = VFB + 2φF + γ 2φF ) quando VS = 0 e cioè
quando la tensione tra source e substrato è nulla VSB = 0 .
Mettendo in relazione le due espressioni si soglia si può scrivere
VTH = VTH0 + γ ( 2φF + VSB − 2φF )
Quindi VTH = VTH 0 se VSB = 0
Mentre se questo non succede, cioè se VS > VB la tensione di soglia cresce come la radice quadrata di
VSB e per ottenere un canale occorre applicare una tensione maggiore al gate.
Tale effetto si chiama effetto BODY.
Effetto substrato (body)
Per misurare la variazione di VT dovuta alla polarizzazione VSB tra source e substrato si utilizza la
configurazione in figura.
Applicando una polarizzazione inversa tra source e substrato si riduce la densità di carica libera nel
canale e quindi nel mosfet a canale n la VTH aumenta (diviene più positiva).
Nel caso di substrato con concentrazione costante ho una
2ε s qN A
ΔVTH =
2φF + VSB − 2φF = γ 2φF + VSB − 2φF
Cox
(
Dove γ =
2ε s qN A
) (
)
è il fattore di effetto substrato ed è espresso in V
1
2 ed è utilizzato per calcolare
Cox
ΔVTH in presenza di una polarizzazione VSB .
In realtà per ottenere una ΔVTH precisa occorre un modello bidimensionale della carica spaziale e non
monodimensionale come quello usato.
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-14
Effetti della carica nell’ossido
La carica presente nell’ossido ed alle sue superfici (si forma soprattutto una carica superficiale tra
ossido e silicio di tipo positivo a causa dei processi di lavorazione), se in concentrazioni confrontabili
con le densità dei portatori in gioco, può dare luogo ad effetti non voluti .
Infatti tale carica induce cariche uguali ed opposte nel metallo e nel semiconduttore.
Al di sopra della soglia la densità superficiale di elettroni è dello stesso ordine di grandezza della
densità degli accettori N A :
2
Qn
∼ NA 3 ,
q
per N A = 1015 cm−3 ⇒
Qn
" 1010 cm−2
q
2
mentre la densità superficiale di atomi di silicio è pari a (5 ×1022 ) 3 = 1.3 ×1015 cm−2
Quindi la densità superficiale che è 5 ordini di grandezza inferiore alla densità superficiale di atomi di
silicio è sufficiente a modificare il comportamento del sistema MOS
Valori tipici della densità superficiale di carica nell’ossido sono < 1010 cm−2 , ma questa carica è
comunque sufficiente a modificare la carica immagazzinata all’equilibrio nel sistema MOS e quindi la
tensione di banda piatta VFB secondo la relazione
ΔVFB
1
=−
C 'oss
xoss
∫
0
x
ρ ( x)dx
xoss
dove ρ ( x) è la distribuzione arbitraria di carica nell’ossido.
Considerando anche una carica Q 'ss per unità di area all’interfaccia Ossido-Silicio ed il suo contributo
Q'
ΔV 'FB = − oss si ha
C 'oss
VFB = φMS
Q'
1
− oss −
C 'oss C 'oss
xoss
∫
0
x
ρ ( x)dx
xoss
Il contributo principale è di solito la carica all’interfaccia −
Dispositivi Elettronici – Capitolo VI: Il MOSFET
Q 'oss
C 'oss
VI-15
Condensatori MOS e dispositivi ad accoppiamento di carica (CCD)
Le applicazioni più immediate del sistema ossido silicio sono:
• Condensatori di alta qualità e di precisione controllata per
o Conversione A/D (confronto con una tensione di riferimento di livello
crescente/decrescente mediante una matrice lineare di condensatori le cui capacità sono
ciascuna la metà della precedente
o Il dispositivo ad accoppiamento di carica (charge-coupled device – CCD)
Dispositivi ad accoppiamento di carica (charge-coupled device – CCD)
Sono matrici di condensatori MOS ad alta densità utilizzati come rivelatori ottici in macchine
fotografiche e telecamere o come memorie. Possono memorizzare anche segnali analogici (la quantità
di carica accumulata non è discreta).
Nei CCD ottici la generazione dei portatori è arricchita dalla luce incidente.
La polarizzazione di base è in condizione di svuotamento profondo.
Ogni pixel ha dimensioni dell’ordine dei 10 micron ed il chip completo è di ½ o 1/3 di pollice di lato.
Quindi i condensatori sono affiancati l’un all’altro e la carica libera immagazzinata nello strato di
inversione è trasferita nel pixel vicino mediante le tensioni di gate.
La capacità del sistema varia da Cox quando la popolazione è generata in equilibrio sino a valori molto
bassi, cioè quando sovrapponendo un segnale ad alta frequenza la popolazione non riesce a seguire il
segnale
L’idea alla base del CCD è che se la polarizzazione del gate (al metallo) è maggiore della soglia
VG > VT , allora il canale può essere caricato a qualsiasi densità di carica compresa tra 0 (in condizione
di svuotamento profondo) e Qn (condizione di equilibrio termodinamico).
Tale carica e cioè il segnale può poi essere trasferito da un pixel a quello adiacente mediante una
strategia a shift register (registro di scorrimento).
C’è una velocità minima di trasferimento che deve essere superiore alla velocità di generazione sulla
superficie svuotata del silicio. Infatti non riesco a mantenere a lungo la regione svuotata lungo il
canale a causa del rumore di generazione termica.
Quindi il segnale deve essere trasferito velocemente.
Il trasferimento del segnale è illustrato in figura che illustra tre pixel adiacenti.
Se applico al gate centrale una tensione positiva V2 > V1 ,V3
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-16
Si forma sotto il contatto 2 una regione invertita.
Se voglio trasferire questo segnale facendolo scorrere tra pixel adiacenti allora applico V3 > V2 > V1 ,
creo una regione invertita sotto il contatto 3 che prende gli elettroni dalla regione invertita sotto il
contatto 2, cioè trasferisco gli elettroni dal contatto 2 al 3. Ridiminuendo la tensione V2 sino a
V1 trasferisco completamente la carica e quindi il segnale.
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-17
Il transistor MOSFET
In figura è illustrata la struttura fondamentale di un MOSFET a canale n anche detto nMOS.
I tre terminali del dispositivo sono source (S), drain (D) e gate (G). E’ poi di solito presente un quarto
terminale che collega il substrato: body (B).
Le giunzioni di source e drain sono realizzate mediante diffusione e sono isolate elettricamente sino
alla formazione dello strato di inversione la cui formazione è controllata dal gate.
Quando la superficie del silicio è invertita (cioè c’e’ un canale tra S e D) l’applicazione di una
tensione VDS porta ad un campo elettrico che forza degli elettroni entranti in S ad arrivare in D.
Nel caso dell’nMOS la corrente è di elettroni che sono maggioritari.
I simboli dei MOS sono illustrati in figura. (a) mostra dei MOSFET simmetrici con la freccia che
indica il verso della corrente verso il substrato (è la rappresentazione più corretta). (b) e (c) sono molto
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-18
usati in pratica (la polarizzazione del substrato è molto bassa nell’nMOS e alta nel pMOS per
polarizzare inversamente la giunzione diffusa). (d) è la tipica rappresentazione dei circuiti digitali
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-19
Correnti nei MOSFET
Nei MOSFET L è la lunghezza di canale che determina il processo tecnologico per la fabbricazione.
Allo stato attuale in produzione si è arrivati a 65 nm.
W è la larghezza di canale (profondità). Dato L si determina W per avere una precisa conduttanza.
xoss è lo spessore dell’ossido il cui valore tipico sta sempre più diminuendo per la necessità di avere
tecnologie sempre più spinte. Allo stato attuale si utilizzano materiali ad alto K (costante dielettrica)
per ottenere spessori dell’ossido di pochi nanometri che siano in grado comunque di isolare
elettricamente il gate dal canale.
Il MOS considerato finora con substrato p e regioni diffuse di source e drain di tipo n + è a canale n o
nMOS.
Il dispositivo complementare con substrato n e regioni S e D di tipo p + è detto a canale p o pMOS.
Le giunzioni formate dalle regioni diffuse con il substrato devono sempre essere polarizzate
inversamente per non avere correnti parassite
Si possono distinguere 3 regioni:
1. regione di interdizione ( VGS < VTH ): in questa regione la densità di carica di canale in
prossimità del source è nulla; dunque vale anche VGD < VTH . In queste condizioni il canale non
è formato è la corrente di drain I D = 0 . Nell’nMOS le cariche vengono allontanate
dall’interfaccia O-silicio comincia a comparire uno strato di inversione costituito pero’ da
cariche fisse (ioni) e quindi non è possibile la conduzione
2. Regione di triodo o lineare ( VGS > VTH e VGD > VTH ): in questa regione il canale esiste sia in
prossimità del source che del drain e la corrente scorre per effetto campo in modo linearmente
dipendente dalla tensione applicata VDS .
3. Regione di saturazione ( VGS > VTH e VGD < VTH ): La carica non è presente su tutto il canale ma
si ferma in L ' . La I D > 0 e non è più linearmente dipendente da VDS .
Di solito si preferisce esprimere le condizioni in funzione di VDS . Poiché VGS − VDS = VGD . Quindi
posso riscrivere le condizioni:
• In zona triodo o lineare VDS < VGS − VTH
• In saturazione VDS > VGS − VTH
Il confine tra le due regioni di funzionamento è dato da :
VDSSAT = VGS − VTH
Regione di triodo o lineare
Suppongo di applicare una tensione VG > VTH e una VDS tra D e S piccola e positiva in modo da avere
una generazione di carica nel canale che non vari molto con la posizione lungo il canale. Qc ( y )
comunque diminuisce muovendosi dal S al D.
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-20
se VS = VB = 0 e VG aumenta creo una regione di svuotamento. Aumentando ulteriormente VG , il
livello di Fermi all’interfaccia O-S supera il livello intrinseco Ei creando la regione di inversione e
quindi il canale tra S e D.
A tensioni VG ancora superiori si raggiunge la condizione di forte inversione ed ulteriori aumenti non
danno luogo a sensibili variazioni della carica della regione svuotata Qd .
La concentrazione Qc di elettroni nello strato di inversione varia linearmente con la tensione di
overdrive (VG − VTH ) :
Qc ∝ (VG − VTH )
Lo stesso andamento si ha per la corrente I D tra drain e source.
La corrente di drain I D , che è una corrente di deriva (generata da un campo elettrico), è legata alla
carica totale del canale QC attraverso il tempo di transito:
Q
ID = − C
Ttr
Dove
L
Ttr =
vd
dove vd è la velocità di deriva.
vd = −µ nε y = µ n
(VD −VS )
V
= µ n DS
L
L
quindi il tempo di transito si può riscrivere come
L2
Ttr =
µnVDS
Si vedrà che la mobilità del canale di superficie µ n è di solito pari ad una frazione di quella nel
volume.
Considerando le dimensioni del canale e sapendo che la densità di carica mobile all’interfaccia ossidosilicio è
Qc = −Cox (VG − VTH )
posso calcolare la carica totale del canale
QC = QcWL = −Cox (VG − VTH )WL
che sostituita nell’espressione della corrente I D :
I D = − µn
W
Cox (VG − VTH )VDS
L
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-21
Per VDS piccola, l’andamento della corrente è pertanto lineare con la tensione applicata e la quantità
W
− µn Cox (VG − VTH ) è la conduttanza del canale che dipende dalla tensione di overdrive (VG − VTH ) .
L
Se aumento VDS , questa relazione non è più valida poiché riduco la carica di canale QC in prossimità
del drain (dove la tensione tra gate e volume viene ridotta).
Altra formulazione
La concentrazione degli elettroni è dipendente dalla posizione n = n( x, y ) .
Quindi la densità di carica può essere ottenuta integrando la concentrazione di elettroni lungo l’asse x.
Con una rappresentazione tridimensionale come in figura ed ipotizzando che in un punto di ordinata y,
il canale si estenda lungo l’asse x tra 0 e xc si può scrivere
Qc ( y) =
xc ( y )
∫
−qn( x, y)dx
0
La densità di corrente di deriva lungo y può essere riscritta come
dV ( y)
jn (x, y) = qµ n n(x, y)ε y = −qµ n n(x, y) c
y
dy
La corrente di drain è ottenuta integrando la densità di corrente jn y sulla superficie A(y) mostrata in
figura (W è costante e può essere portato fuori dall’integrale).
ID = W
xc ( y )
∫
x =0
− jny ( x, y )dx
Il segno meno tiene conto del fatto che I D scorre in senso opposto al verso dell’asse y.
⎛ xc ( y )
⎞ dV ( y)
I D = − µnW ⎜ ∫ −qn( x, y )dx ⎟ c
⎜
⎟ dy
⎝ x =0
⎠
quindi poiché il termine tra parentesi è Qc ( y )
dV ( y)
I D = − µnWQc ( y) c
dy
Integrando lungo y tra 0 e L (integro ambo i membri).
L
dV ( y )
I D L = − µnW ∫ Qc ( y ) c
dy
dy
y =0
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-22
divido per L e cambio variabile di integrazione
V ( L ) =VD
W c
I D = − µn
Qc ( y )dVc ( y )
L Vc (0)∫=VS
sostituisco Qc ( y) = −Cox [VG − VTH − Vc ( y )]
ed ottengo
V ( L ) =V
D
W c
[VG − VTH − Vc ( y )]dVc ( y )
L Vc (0)∫=VS
la cui soluzione è
VD2 −VS2 %
W"
I D = µ nCox $(VG −VTH )VDS −
'
L $#
2 '&
tenendo conto che
VD2 − VS2 = (VD + VS )VDS e VG = VGS + VS l’espressione precedente diviene
I D = µnCox
2 %
VDS
W"
I D = µ nCox $(VGS −VTH )VDS −
'
L $#
2 '&
Questa relazione individua un fascio di parabole passanti per l’origine degli assi. Il massimo di ogni
parabola può essere trovato annullando la derivata della relazione rispetto a VDS
dI D
W
= µnCox (VGS − VTH − VDS ) = 0
dVDS
L
⇒
VGS − VTH = VDS
Il luogo dei punti si ottiene sostituendo questo valore nella I D , e si ottiene
µC W 2
I D = n ox VDS
2 L
per una VDS piccola l’andamento è lineare e la I D si può approssimare con
W
I D ≈ µnCox (VG − VTH )VDS
L
che approssima il MOSFET con una resistenza controllata dalla tensione VGS
1
RMOS (VGS ) =
W
µnCox (VG − VTH )
L
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-23
L’andamento grafico della caratteristica per diversi valori della tensione di overdrive è illustrato in
figura.
Ho la massima pendenza vicino l’origine dove l’andamento può essere considerato lineare e vale la
W
I D0 = − µn Cox (VG − VT )VDS
L
Per valori più elevati di VD , la carica di canale e quindi la conduttanza diminuisce quindi si ha
l’andamento parabolico con il massimo per VDS = VG − VT .
Al di là di questo punto l’andamento parabolico non è più valido poiché avrei una conduttanza
∂I
incrementale negativa D < 0 che non ha senso dal punto di vista fisico.
∂VD
Regione di saturazione
Un incremento della tensione VDS causa la diminuzione della carica di canale in prossimità del drain
ed accentua la pendenza del profilo del canale che per un certo valore di VDS = VDSSAT si strozza. Questa
è la condizione di pinch-off per cui ad una certa tensione VDS la carica di canale si annulla in
prossimità del drain.
Incrementando ulteriormente la tensione VDS il transistor entra in regione di saturazione ed il punto
dove la carica si annulla si sposta verso il source, per cui il canale non è più lungo L ma L ' .
In questa situazione una porzione della tensione VDS cade ai capi del canale di conduzione (cioè tra 0
e L ' ) e la restante parte tra L ' e L .
Poiché Qc ( L ') = 0 , la tensione di canale in L ' è proprio Vc ( L ') = VG − VTH .
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-24
Sottraendo a questa relazione la tensione VS ottengo la caduta di tensione tra source e L '
Vc ( L ') − Vc (0) = VGS − VTH = VDSSAT
la restante porzione cade sulla zona senza canale tra L ' e L , cioè VDS − VDSSAT
In questo dominio (cioè prima della strozzatura) con VDS > VG − VTH la corrente è determinata dal
campo elettrico dovuto alla caduta di potenziale VDSSAT tra 0 e L ' . I portatori che raggiungono L '
vengono poi accelerati dal campo elettrico dovuto a VDS − VDSSAT che cade sulla restante regione a
velocità limite di deriva vlim .
I D dipende dalla velocità con cui gli elettroni arrivano in L ' che dipende da VDSSAT che essendo
costante rende anche I D costante.
Per VDSSAT = (VG − VTH )
⇒
VDSAT = (VG − VTH ) + VS
in L ', Qc = 0 ⇒ VC ( L ') = VDSAT
per VD > VDSAT posso calcolare I DSAT sostituendo la VDSSAT = VGS − VTH e L ' a L nell’espressione
W
I D = µnCox
L
2
⎡
⎤
VDS
⎢(VGS − VTH )VDS −
⎥
2 ⎦
⎣
e ottengo
W
(VGS − VTH )2
2L '
soglia al source.
I DSAT = µnCox
con VTH
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-25
In ipotesi di canale lungo (alcuni micron) L ' ed L non sono molto differenti, L ' ; L e
I DSAT = µnCox
W
(VG − VTH ) 2
2L
Modulazione della lunghezza di canale
Finora abbiamo considerato la lunghezza di canale L = L ' costante. In realtà L è funzione della
tensione VDS applicata e diminuisce al crescere di VDS con conseguente aumento di I D .
La variazione di I D con VDS in regime di saturazione può essere ricavata da
∂I D µ nCox
I dL'
d 1
.
=
W (VGS −VTH ) 2
=− D
∂VDS
2
dVDS L'
L' dVDS
La lunghezza di canale diminuisce all’aumentare di VDS , quindi la variazione di corrente è positiva (la
corrente aumenta).
⎛ ∂I ⎞
Dunque I D = I D VDS =VDS + ⎜ D ⎟
⋅ (VDS − VDSSAT )
SAT
∂
V
DS
⎝
⎠VDS =VDSSAT
Il primo termine del secondo membro è la corrente già vista per VDS = VDSSAT
L’espressione precedente si può riscrivere sostituendo le relazioni trovate
ID = ID
VDS =VDSSAT
⋅ ⎡⎣1 + λ (VDS − VDSSAT ) ⎤⎦ ,
dove λ = −
1 dL
L dVDS
è il parametro di modulazione di canale.
Quando VDS > VDSSAT l’espressione tra parentesi tonde si può approssimare a VDS
I DSAT =
µnCox W
2
L
(VG − VTH )2 (1 + λVDS ) =
K
(VG − VTH ) 2 (1 + λVDS )
2
con
0.1 < λ < 0.01 V −1
λ è un valore empirico ed ha una forte analogia con la tensione di Early VA nel BJT; di solito
Dispositivi Elettronici – Capitolo VI: Il MOSFET
1
λ
< VA .
VI-26
Parametri del MOSFET
Per una misura sperimentale dei parametri del MOSFET si corto-circuitano il gate ed il drain e si
misura la corrente I D al variare di VD con il source a massa.
Poiché VD = VG deduco dalla condizione di saturazione VDS > VG − VTH che il transitor è in saturazione
e si applica dunque la relazione
I DSAT = k '
W
k
k
(VG − VTH )2 = (VG − VTH ) 2 = (VD − VTH ) 2
2L
2
2
quindi il grafico di
I D vs VD è lineare
Dall’intercetta sull’asse x posso calcolare la tensione di soglia VTH mentre dalla pendenza ricavo
K
.
2
In funzione del processo spesso si definisce una soglia diversa: ad es. la VG per cui I D = 1µ A quando
L = 1µ m e VDS = 1V .
Dall’espressione I D = −µ n
W
C (V −V )V valida in zona lineare e per VDS → 0 , posso calcolare
L ox G TH DS
W
e quindi l’effettiva mobilità del canale. Spesso si ripete la misura per diverse tensioni VG per
L
aver un valor medio affidabile.
µnCox
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-27
Transconduttanza
L’amplificazione di un MOSFET in piccolo segnale dipende dalla transconduttanza. Nella regione per
2 %
VDS
W"
I
!
µ
C
(V
−V
)V
−
,
$
' e la transconduttanza
VD < VDSAT
D
n ox
L $# G TH DS 2 '&
∂I
W
g m = D = µnCox VDS
∂VG
L
In saturazione VD > VDSAT
W
(VGS − VTH )2 (1 + λVDS ) = k (VGS − VTH ) 2 (1 + λVDS )
2L
ID
W
g m = µCox (VGS − VTH ) = 2k (VGS − VTH ) = 2
L
(VGS − VTH )
I D = µCox
da cui si evince che g m è indipendente da VD ed è linearmente dipendente da VG .
Se uso per la corrente di saturazione l’espressione
ID
SAT
=k'
W
k
(VG −VTH ) 2 = (VG −VTH ) 2
2L
2
ottengo
gm
SAT
=k'
W
(V −V )
L G TH
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-28
Modello di piccolo segnale per bassa frequenza
Quando il transistor viene utilizzato per la realizzazione di amplificatori esso lavora in regione di
saturazione. Nei circuiti digitali il transistor viene invece fatto commutare tra regione di triodo e
interdizione. Se usato invece come resistore controllato il MOSFET opera in zona triodo.
Regione di saturazione
Il punto di lavoro Q del transistor definisce VGS ,VDS e I D . Individuato il punto di lavoro che
corrisponde ad un particolare punto della caratteristica I D vsVDS l’analisi si limita alla variazione delle
grandezze elettriche rispetto a questo punto di lavoro a condizione che il dispositivo permanga nella
regione di saturazione.
Se sono in saturazione dunque vale
µC W
iD = n ox (vGS − vTH ) 2 (1+ λ v DS )
SAT
2 L
Quindi la corrente è funzione di vGS , vDS e vSB (poiché la tensione di soglia vTH dipende anche da vSB ).
Quindi la corrente incrementale di drain si può sviluppare in serie di Taylor come
∂i
∂i
∂i
id = D Q ⋅vgs + D Q ⋅vds + D Q ⋅vsb
∂vGS
∂vDS
∂vSB
che esprime il legame lineare tra la variazione della corrente di drain id e le tensioni incrementali vgs ,
vds e vsb .
Da un punto di vista circuitale
Definendo
∂i
gm = D
∂vGS
Q
−1
⎛ ∂i
⎞
rd = ⎜ D Q ⎟
⎝ ∂vDS ⎠
∂i
g mb = − D Q
∂vSB
e sostituendo il generatore di corrente pilotato dalla tensione ai suoi capi si semplifica il circuito
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-29
g m è la transconduttanza di piccolo segnale del transistor e nell’ipotesi di λ piccolo si calcola
µC W
derivando rispetto a vGS la iD ! n ox (vGS − vTH ) 2
SAT
2 L
W
g m = µnCox (VGS − VTH )
L
la transconduttanza si può anche esprimere in funzione di I D o di VDSSAT :
g m = 2µnCox
gm =
W
ID
L
2I D
ID
=
VGS − VTH VDSSAT
2
rd è la resistenza intrinseca di drain e si calcola derivando la iDSAT =
⎛ ∂i
rispetto a vDS ( rd = ⎜ D
⎝ ∂vDS
−1
Q
⎡ µC W
rd = ⎢λ n ox (vGS − vTH ) 2
2 L
⎣
2
L
(vGS − vTH )2 (1 + λ vDS )
⎞
⎟ ):
⎠
−1
1
⎤
=
Q⎥
µC W
⎦
λ n ox (VGS − VTH ) 2
2 L
se sostituisco l’espressione approssimata per iDSAT cioè iD
SAT
rd =
µnCox W
!
mnCox W
(vGS − vTH )2 ottengo
2 L
1
λID
Il parametro g mb è la transconduttanza di effetto body che in genere ha un valore pari al 10÷20% di
g m ed in genere viene trascurata.
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-30
Effetti capacitivi nel MOSFET
Gli effetti capacitivi in buona parte sono legati al processo tecnologico.
Una schematizzazione del MOS integrato è mostrata in figura, che illustra il layout e la sezione del
dispositivo.
Il gate è normalmente in polisilicio e si può osservare dalla sezione che le regioni diffuse si insinuano
al di sotto del gate per una lunghezza LD creando delle regioni di overlap di area pari a WLD . Di
conseguenza si ha una diminuzione dell’effettiva lunghezza di canale che non è più L ma Leff
Vediamo le diverse capacità in gioco illustrate in figura.
Capacità Gate-Canale
E’ la capacità C g ,ch tra il terminale di gate ed il canale pari a Cg ,ch = −
∂Qc
dove Qc è la carica totale
∂VG
del canale.
La Qc si ottiene integrando la Qc ( y ) lungo il canale sino a L ' :
L'
Qc = W ∫ Qc ( y )dy = W
0
Vc ( L ')
⎡ dy ⎤
Qc ( y ) ⎢
⎥ dVc ( y )
dV
(
y
)
c
⎣
⎦
Vc (0) =VS
∫
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-31
come già visto Vc ( L ') = VG − VTH inoltre dalla I D = − µnWQc ( y )
µ WQ ( y )
dy
=− n c
dVc ( y )
ID
da cui Qc = −
µnW 2
Vc ( L ') =VG −VTH
ID
∫
[Qc ( y)]
2
Vc (0) =VS
Risolvendo l’integrale si ottiene Qc = −
ID =
dVc ( y ) = −
µn (CoxW )2
3I D
µnCox W
2
µnCox2 W 2
ID
dVc ( y)
trovata in precedenza ottengo
dy
Vc ( L ') =VG −VTH
∫
[VG − VTH − Vc ( y)]
2
dVc ( y )
Vc (0) =VS
(VGS − VTH )3 per cui sostituendo la corrente
2
(VGS − VTH )2 , la carica totale risulta Qc = − CoxWL(VGS − VT ) che derivata porta a
L'
3
Cg ,ch =
∂QN 2
= CoxWL
∂VG 3
Capacità di overlap
Da considerazioni geometriche si ottiene che la capacità di overlap è pari a
Cov = CoxWLD dove Cox =
ε ox
è la capacità per unità di area dell’ossido.
tox
Da un punto di vista elettrico vengono considerate collegate tra il gate e i terminali di source e drain.
Capacità di giunzione
L’ultimo contributo è dovuto alle capacità di svuotamento delle giunzioni source-substrato e drainsubstrato. Il calcolo di queste capacità è leggermente differente da quello delle giunzioni pn.
Si consideri la schematizzazione in figura.
Tutte le facce della regione diffusa sono a contatto con il substrato eccetto la superiore.
L’area della giunzione è formata dalla superficie inferiore più le tre superfici laterali non a contatto
con il canale (quella verso il canale è a contatto con le cariche mobili di canale e non con quelle fisse
della regione svuotata).
Il contributo delle facce inferiori per source e drain è:
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-32
C js =
C jd =
C j0 Aj
(1 + VSB / Vbi )
mj
C j0 Aj
(1 + VDB / Vbi )
mj
dove C j0 è la capacità della giunzione per unità di superficie in assenza di polarizzazione (valutata in
genere sperimentalmente) e Aj = WL j l’area della giunzione (superficie inferiore), m j è un coefficiente
empirico compreso tra ½ e 1/3. Vbi =
kT ⎛ N Ddiff N AB
ln ⎜
q ⎜⎝ ni 2
⎞
⎟⎟ .
⎠
Per giunzioni brusche si può assumere m j = 1/ 2 e C j0 ≈
qε s N AB
2Vbi
.
Allo stesso modo per le giunzioni laterali:
C jssw =
C jdsw =
C j0 Ajsw
(1 + VSB / Vbi )
mj
C j0 Ajsw
(1 + VDB / Vbi )
mj
dove Ajsw = x j (2 L j + W )
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-33
Modello di piccolo segnale per alta frequenza
Modello in regione di saturazione
Nel modello ad alta frequenza occorre includere gli effetti capacitivi.
Il modello risultante in regione di saturazione è illustrato in figura.
Vi sono quattro capacità :
• La capacità C gs tra gate e source è generata da due contributi in parallelo
o Capacità di overlap tra gate e source
o Capacità tra gate e canale C g ,ch
Quindi
2
2
Cgs = Cg ,ch + Cov = CoxWL + CoxWLD ≈ CoxWL
3
3
l’approssimazione è valida in quanto L  LD
•
La capacità C gd tra gate e drain è generata dal solo contributo di overlap:
Cgd = Cov
•
Le restanti capacità Csb e Cdb sono connesse tra le regioni diffuse di drain e source ed il
substrato e sono causate dalla polarizzazione inversa delle giunzioni. Esse dipendono dalle già
viste capacità di giunzione:
Csb = C js + C jssw
o
Cdb = C jd + C jdsw
Modello in regione di interdizione
In regione di interdizione sebbene tra source e drain vi sia un circuito aperto, ad alta frequenza ci
possono essere effetti capacitivi che conviene considerare nella modellistica del dispositivo.
Le capacità di overlap continuano ad essere presenti indipendentemente dalla regione di
funzionamento.
La capacità gate-canale ovviamente è assente.
Esiste invece una capacità tra gate e substrato che per piccolo segnale può essere definita come la
derivata della carica totale di gate QGWL rispetto alla tensione gate-substrato:
∂Q
C gb = G WL
∂VG
Se si trascurano gli effetti delle due regioni diffuse e si ipotizza che il transistor si comporti come un
condensatore MOS allora nelle diverse regioni:
• in accumulazione( VG < VFB ): Cgb = CoxWL
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-34
•
in regime di svuotamento o debole inversione: la carica nel gate è uguale ed opposta a quella
immagazzinata nel substrato (carica svuotata Qd ):
⎛ ∂Q ⎞⎛ ∂φ ⎞
∂QG
∂Q
WL = − d WL = ⎜ − d ⎟⎜ s ⎟WL
∂VG
∂VG
⎝ ∂φs ⎠⎝ ∂VG ⎠
⎛ ∂Q ⎞
dove il termine ⎜ − d ⎟ è una capacità Cd che rappresenta la variazione della carica di svuotamento
⎝ ∂φs ⎠
Cgb =
rispetto al potenziale superficiale che si ottiene derivando la Qd = −qN AB xd = − 2qε s N AB φs .
⎛ ∂Q
Cd = ⎜ − d
⎝ ∂φs
2qε s N AB
⎞
⎟=
2 φs
⎠
2qε s N AB φs
∂φ s
Q
si ricava derivando la VGB − VFB ≈ φs − d = φs +
(che si è visto
∂VG
Cox
Cox
essere valida in regione di svuotamento e con buona approssimazione in debole inversione):
∂VG
C
1 2qε s N AB
= 1+
= 1+ d
∂φs
Cox 2 φs
Cox
mentre il termine
invertendo questa relazione e sostituendo si ottiene
C gb = C ox  C d WL
(
)
Il circuito equivalente quindi è in regione di interdizione
dove oltre alla capacità C gb appena trattata esistono le capacità C gs e C gd che sono date
esclusivamente dalla capacità di overlap, e le capacità Csb e Cdb che sono le capacità di giunzione già
discusse.
Modello in regione di triodo
E’ un caso simile alla regione di saturazione ma in questa regione la corrente è pari a
V2 ⎤
W⎡
I D = µnCox ⎢(VG − VT )VDS − DS ⎥ .
L⎣
2 ⎦
In questo caso rd si riduce rispetto al valore in saturazione e rende trascurabile il contributo degli altri
generatori pilotati. Si ha dunque l’equivalenza del MOSFET con un resistore comandato da VGS
1
rd =
W
µnCox (VG − VTH )
L
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-35
Per quel che riguarda gli effetti capacitivi sono presenti le capacità Csb e Cdb che sono le capacità di
giunzione, e le due capacità C gs e C gd .
Non è presente la capacità C gb poiché la presenza del canale elimina effetti capacitivi tra gate e
substrato.
Mentre esiste la capacità C g ,ch di canale. Essendo la carica totale pari a QN = QnWL = Cox (VGS − VT )WL
si ottiene
C g ,ch = CoxWL
Questa capacità è di solito arbitrariamente assegnata per metà a C gs e metà a C gd . Per cui
1
Cgs = Cgd = Cov + CoxWL
2
Il modello risultante è perciò
Quindi ricapitolando
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-36
Effetti di campo elevato nel MOSFET
Mobilità superficiale e campo verticale
La mobilità µ n vista finora e usata per ricavare il modello del MOSFET non è la mobilità degli
elettroni misurata all’interno del cristallo di silicio che è una mobilità di substrato. In realtà è una
mobilità di superficie che può discostarsi sensibilmente da quella di substrato e che tiene conto del
fatto che gli elettroni, viaggiando in una regione prossima alla interfaccia con l’ossido subiscono un
ulteriore disturbo. L’interazione dei portatori con l’ossido dipende molto dal campo elettrico verticale
che aumenta il disturbo attirando i portatori verso l’interfaccia. Esiste una relazione empirica che lega
la mobilità superficiale µ n al campo elettrico verticale x :
µn =
ε
µn
1 + Θε x
dove µ n0 è il valore che la mobilità di superficie assume in assenza di campo elettrico verticale e Θ è
0
un coefficiente denominato fattore di riduzione della mobilità ed è dell’ordine dei 1.5 ×10−6 cm / V .
La relazione che lega la mobilità superficiale media µ s con quella in assenza di campo elettrico
verticale è data con buona approssimazione da
µs ≈
µn
0
1 + θ (VGS − VT )
dove θ = Θ
Cox
2ε s
Campo laterale e mobilità effettiva
Sinora si è visto che il moto dei portatori è dovuto al campo elettrico per effetto della tensione
applicata VDS , considerando una dipendenza lineare tra velocità di deriva e campo elettrico applicato.
Questa dipendenza è valida solo per piccoli campi elettrici.
Per campi elettrici intensi, oltre un certo valore critico c la velocità dei portatori satura raggiungendo
un valore critico denominato velocità di saturazione vmax .
ε
Per gli elettroni nel silicio vmax = 107 cm / s
Per campi piccoli dunque I D = − µnWQn ( y )
Dispositivi Elettronici – Capitolo VI: Il MOSFET
dVc ( y )
dy
VI-37
ε
ma la variazione del potenziale di canale lungo il canale è pari al campo elettrico −
I D = µ nWQn ( y )ε y
y
Qn tende a zero in prossimità del drain, ma essendo la corrente costante su tutto il canale, si ha che il
campo elettrico cresce moltissimo e causa la saturazione della velocità dei portatori.
Il campo critico ε c è definito dove la retta vn = µn (−ε y ) si interseca con la retta vn = vmax , quindi il
campo critico si definisce
ε c = vµmax
n
La relazione empirica che lega la velocità dei portatori al campo elettrico è
−ε y
vn = vmax
ε
1+
−ε y
c
ε
c
la densità di corrente è legata alla velocità dalla relazione jn = −qnvn che porta alla relazione
I D = −WQc ( y)vn ( y)
Integrando tra source e drain si ottiene l’espressione finale che è
⎡
⎤
⎢
⎥
µn
⎢
⎥ C W (V − V − VDS )V
ID =
ox
GS
T
DS
⎢⎛
L
2
VDS ⎞ ⎥
⎢ ⎜1 +
⎟⎥
⎢⎣ ⎝ L ⋅ ε c ⎠ ⎥⎦
L’effetto immediato della saturazione della velocità è di ridurre la corrente di drain.
In molti casi si parla di una mobilità effettiva definita dalla espressione sotto parentesi quadra.
Unendo l’effetto del campo verticale con quello del campo laterale si definisce una mobilità effettiva
µn =
eff
µn
0
⎛
V
[1 + θ (VGS − VT )] ⎜1 + L ⋅DSε
⎝
c
⎞
⎟
⎠
che è spesso utilizzata nella modellistica dei MOSFET.
Un altro effetto della saturazione della velocità è quello di ridurre la tensione drain-source di
saturazione rispetto al valore previsto VDSSAT = VGS − VTH al valore
⎡
2(VGS − VTH ) ⎤
VDSSAT = Lε c ⎢ 1 +
− 1⎥
Lε c
⎥⎦
⎣⎢
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-38
Effetto canale corto
La possibilità di ridurre le dimensioni dei MOSFET porta a molti vantaggi:
• riduzione delle dimensioni del chip
• aumento della densità dei transistor e della potenza di calcolo
• riduzione dei costi grazie all’aumento del numero di chip per wafer
• maggiori frequenze di funzionamento
Questi risultati si ottengono grazie alla riduzione della lunghezza minima di canale con l’avanzamento
della tecnologia. Negli ultimi dieci anni questa lunghezza è stata ridotta quasi di un ordine di
grandezza.
La riduzione delle dimensioni è chiamata scaling. Ci possono essere due tipi di scaling:
• scaling a campo elettrico costante: riducendo le dimensioni si cerca di preservare i campi
elettrici all’interno del MOSFET. Si aumentano le concentrazioni di drogante e riducono i
potenziali in gioco. Se la riduzione è di un fattore S , si ha la riduzione sia dell’area che della
potenza dissipata di un fattore S2. Si riduce la tensione di soglia che può diventare talmente
piccola da non consentire lo spegnimento corretto del dispositivo. Le tensioni di alimentazione
sono ridotte di un fattore S che pero’ possono portare a un difficoltoso interfacciamento con il
mondo esterno. I processori possono con questo scaling lavorare a frequenze dei GHz.
• scaling a tensione costante. Si ha un incremento della concentrazione di drogante di un fattore
S2 in modo da preservare le relazioni che legano il campo elettrico alla carica. Anche in questo
caso si ha la riduzione dell’area di un fattore S2 ma la dissipazione di potenza aumenta di un
fattore S. I campi elettrici elevati compromettono però l’affidabilità.
Effetto sulla tensione di soglia
La riduzione delle geometrie non è stata uguale nelle tre dimensioni del transistor.
In particolare la geometria planare (ad es. L, W ) dipendente dalla litografia si è ridotta di più degli
spessori xox o delle regioni diffuse x j .
Uno degli effetti del canale corto è la riduzione della tensione di soglia rispetto al valore previsto
La tensione di soglia in funzione della carica di svuotamento vale
Q
VTH = VFB + 2φF − d
Cox
dove per definizione di tensione di soglia vale Qd = QdMAX = − 2qε s N AB (2φF + VS ) .
Abbiamo sinora considerato la carica di svuotamento costante sotto il canale, in questo caso la carica
totale è Qd = QdWL
Quindi posso scrivere la tensione di soglia come
Qd
VTH = VFB + 2φF −
CoxWL
Nei transistor a canale corto la polarizzazione del source e del drain influenza sensibilmente la
distribuzione di Qd che non può essere assunta uniforme essendo modificata in prossimità delle
regioni diffuse anche dalla polarizzazione inversa delle giunzioni. Quindi la carica di svuotamento
totale va calcolata come
L
Qˆ d = W ∫ Qd dy
0
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-39
Non è facile avere un’espressione analitica della carica di svuotamento e quindi della carica totale Qˆ d
ma si sa che vale sempre Qˆ ≤ Q
d
d
La nuova tensione di soglia è
Qˆ d
VˆTH = VFB + 2φF −
CoxWL
Ricordando inoltre che
QD
= −γ 2φF + VSB ,
CoxWL
dove γ =
2qε s N AB
Cox
e facile verificare che la tensione di soglia si può riscrivere
Qˆ
VˆTH = VFB + 2φF + D γ 2φF + VSB
QD
e la variazione della tensione di soglia è
⎛ Qˆ ⎞
ΔVTH = VˆTH − VTH = − ⎜1 − d ⎟ γ 2φF + VSB
⎜ Q ⎟
d ⎠
⎝
Per ricavare il rapporto
Qˆ d
si consideri la figura (b)
Qd
si ipotizza che source e drain in figura siano allo stesso potenziale e i bordi delle regioni diffuse
cilindrici. In figura sono evidenziate le regioni svuotate di gate e anche di source e drain (tutte estese
xd ).
La carica Qˆ assume un profilo trapezoidale.
d
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-40
Sotto queste ipotesi semplificative il rapporto
Qˆ d
è il rapporto tra le corrispondenti aree di figura (a e
Qd
b)
L + L1
xd
Qˆ D
x
= 2
= 1− L
QD
Lxd
L
dove xL può essere ricavato dal teorema di Pitagora
xd 2 + ( xL + x j )2 = ( x j + xd )2
da cui si ottiene
⎛
⎞
⎞
xj ⎛
2x
Qˆ d
2x
x
xL = x j ⎜ 1 + d − 1 ⎟
⇒
= 1 − L = 1 − ⎜ 1 + d − 1⎟
⎜
⎟
⎟
xj
Qd
L
L ⎜⎝
xj
⎝
⎠
⎠
da cui si ottiene il ΔVTH
per una espressione più semplice e se x j ? xd si approssima
Qˆ d
x
≈ 1 − β1 d
Qd
L
dove β1 è un parametro correttivo tipicamente pari a 1. Quindi poiché per definizione di tensione di
soglia xd è pari al suo valore massimo xd = xdMAX = ς 2φF + VS
dove ς =
2ε s
qN AB
si ottiene
⎛ βς
VˆTH = VFB + 2φF + γ 2φF + VS ⎜1 − 1
L
⎝
β1ςγ
⎞
2φF + VS ⎟
⎠
(2φF + VS )
L
Esplicitando le definizioni di ζ , γ e Cox si ottiene
ε x
ΔVTH = −2β1 s ox (2φF + VS )
ε ox L
Quindi la variazione della tensione di soglia è direttamente proporzionale allo spessore dell’ossido e
inversamente proporzionale alla lunghezza di canale
ΔVTH = −
Effetto della tensione drain-source:Drain Induced Barrier Lowering (DIBL)
Finora abbiamo considerato VDS trascurabile. Aumentando VDS la situazione è quella in figura e vicino
Qˆ
al drain aumenta la regione di carica spaziale a scapito di Qˆ d . Quindi il rapporto d diminuisce e
Qd
quindi anche Vˆ .
TH
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-41
Non ho più una forma trapezoidale ma posso sostituire a xL un valor medio ( xLS + xLD ) / 2 e quindi
posso scrivere
( xL + xLD )
Qˆ d
= 1− S
Qd
2L
⎛
⎞
2 xd S
xLS = x j ⎜ 1 +
− 1⎟
⎜
⎟
xj
⎝
⎠
⎛
⎞
2 xd D
xLD = x j ⎜ 1 +
− 1⎟
⎜
⎟
xj
⎝
⎠
dove le profondità delle regioni svuotate in prossimità del drain e source sono:
xdS = ς 2φF + VS
xd D = ς 2φF + VD
queste espressioni sostituite nel rapporto
Qˆ d
Qd
⎞ ⎛
⎞⎤
2xd
2xd
x j ⎡⎛
Q̂d
S
D
⎢
⎜ 1+
= 1−
− 1⎟ + ⎜ 1+
− 1⎟ ⎥
Qd
2L ⎢⎜⎝
xj
xj
⎟⎠ ⎜⎝
⎟⎠ ⎥
⎣
⎦
(xd + xd )
Q̂d
bV
D
per x j ≫ xd > xd
⇒
≈ 1− b1 S
= 1− 1 ( 2f F + VS + 2f F + VD )
D
S
Qd
2L
2L
Attraverso passaggi algebrici ed espansioni in serie di Taylor si dimostra che
ΔVTH = −2β1
ε s xox
[(2φF + VS ) + β 2VDS ]
ε ox L
di norma β2 = 1/ 4 ma varia con la lunghezza di canale (~1/L)
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-42
Il MOSFET in elettronica
Regione sottosoglia
(Debole Inversione)
La corrente di saturazione dipende dalle tensioni applicate
I s = I D0 e
qVGS
nKT
e
−
Regione
Lineare o di triodo
−
qVBS
nKT
qVDS
I D = I s (1 − e KT )
Regione di lavoro in pacemaker, orologi etc.. (bassissime dissipazione
di potenza)
VGS > VT
VDS < VGS − VT
I D = µCox
W
L
⎡
⎡
VDS 2 ⎤
VDS 2 ⎤
(
V
−
V
)
V
−
=
2
k
(
V
−
V
)
V
−
⎢ GS T DS
⎥
⎢ GS T DS
⎥
2 ⎦
2 ⎦
⎣
⎣
W
2L
W
g m = µCox VDS = 2kVDS
L
1
W
g ds = = µCox (VGS − VT − VDS ) = 2k (VGS − VT − VDS )
ro
L
Il transistor può essere usato come una resistenza controllata:
1
RMOS =
2k (VGS − VT )
k = µCox
Regione di
Saturazione
VGS > VT
VDS > VGS − VT
W
I D = µ Cox
(VGS − VT ) 2 (1 + λVDS ) = k (VGS − VT ) 2 (1 + λVDS )
2L
W
k = µCox
2L
ID
W
g m = µ Cox (VGS − VT ) = 2k (VGS − VT ) = 2
L
(VGS − VT )
1
g ds = = λ I D
ro
se si considerano effetti di ordine superiore si ha
∂I S
∂VT
I D ∂µ
gds = λ I D 1°ordine − gm
canalecorto +
vel .saturazione +
∂VDS
µ ∂VDS
∂VDS
eff .valanga
Caratteristica d’ingresso I D vs VGS in saturazione
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-43
Caratteristica d’uscita I D vs VDS
Calcolo del punto di lavoro
• Si fa un’ipotesi di regione di funzionamento del transistor (lineare, saturazione, interdizione)
• Si verifica l’ipotesi
o Se corretta si prosegue
o Se sbagliata si riparte con un’altra ipotesi
Dispositivi Elettronici – Capitolo VI: Il MOSFET
VI-44