ESERCIZI E COMPLEMENTI DI ANALISI
MATEMATICA: primo foglio
A. Figà Talamanca
3 ottobre 2010
2
0.1
Numeri reali
Diamo per scontato che gli studenti conoscano i numeri razionali. Questi sono
i numeri che possono essere espressi con una frazione cioè come quoziente di
due numeri interi.
Se, come è usuale nei testi di matematica, indichiamo con il simbolo Q
l’insieme dei numeri razionali e con il simbolo Z l’insieme dei numeri interi,
nella notazione della teoria degli insiemi si può scrivere
n
Q = { : n, m ∈ Z, m 6= 0}.
m
Sappiamo che ogni frazione definisce univocamente (basta svolgere la divisione) un decimale, che può essere finito o periodico. Viceversa non è difficile
dimostrare che ogni espressione decimale finita o periodica può scriversi come
il quoziente tra due numeri interi. Ricordiamo che i numeri interi sono costituiti dai naturali, cioè i numeri 1, 2, 3, . . . , il cui insieme si indica con N, e
inoltre dal numero 0 e dai numeri interi negativi, −1, −2, −3, . . . .
Possiamo ricordare che è ben definita la somma ed il prodotto di due
numeri razionali (basta saper sommare e moltiplicare due frazioni) e che è
altrettanto ben definita la relazione d’ordine. Cioè siamo in grado di dire
quando due frazioni n/m e k/h sono l’una maggiore dell’altra.
Esercizio 1 . Mettere in ordine decrescente le seguenti frazioni:
4/5, 5/4, 51/37, 49/31, 37/29
Esercizio 2 Date due frazioni n/m e k/h come si fa a stabilire quale è più
grande e quale è più piccola?
E’ noto che in matematica e specialmente nello studio dell’analisi matematica si considerano numeri cosiddetti irrazionali che non possono essere
espressi come quoziente di due numeri interi. In un certo senso, come vedremo, i numeri razionali non bastano per descrivere tutte le grandezze alle
quali vorremmo associare un numero.
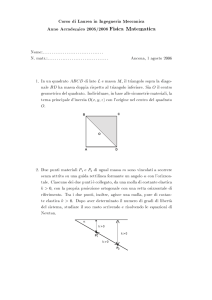
Il caso più semplice di inadeguatezza dei numeri razionali per descrivere grandezze si è presentato circa venticinque secoli fa, quando si cercò di
calcolare la lunghezza della diagonale di un quadrato di lato uno.
Un caso particolare del teorema di Pitagora ci dice che se d è la lunghezza
della diagonale di un quadrato di lato uno, allora d2 = 2.
Possiamo chiederci allora se esiste un numero razionale il cui quadrato è
proprio due. In altre parole possiamo chiederci se esistono numeri interi m
ed n che soddisfino all’equazione
m2 = 2n2 .
0.1. NUMERI REALI
3
Se questi numeri esistessero potremmo supporre che siano positivi e non
ambedue pari (perché?). Osserviamo ora che il quadrato di un numero pari
è pari ed il quadrato di un numero dispari è dispari (perché?). Ne segue che
m non può essere dispari perché il suo quadrato è pari. Ma se m è pari allora
m = 2k per qualche intero k. Dall’equazione precedente segue allora che
4k 2 = 2n2 ,
e quindi
2k 2 = n2 .
Ma allora il quadrato di n è pari, da cui segue che n è pari. Quindi sia n che
m sono pari il che contraddice la nostra ipotesi.
Abbiamo cosı̀ dimostrato che nessun numero razionale può avere come
quadrato 2.
Esercizio 3 Rispondere ai ”perché?” indicati in parentesi nella dimostrazione
che precede.
Furono quindi gli antichi greci a scoprire che non tutte le ”grandezze” che
si presentavano naturalmente nello studio della geometria potevano essere
espresse attraverso rapporti tra numeri interi. Fu sviluppata allora la teoria
delle grandezze cosiddette incommensurabili, che prefigura, almeno dal punto
di vista concettuale, la moderna teoria dei numeri reali.
Nelle trattazioni ”moderne”, anziché partire dallo studio delle grandezze
geometriche si preferisce partire dall’insieme Q dei numeri razionali cercando di ”completarlo” con l’aggiunta di una congrua quantità di numeri
irrazionali.
Un modo apparentemente semplice di operare questa integrazione dell’insieme Q è quello di partire dalla forma decimale dei numeri razionali ed
aggiungere tutti i decimali infiniti che non sono periodici e che quindi non
corrispondono a numeri razionali.
Questa scorciatoia, adottata anche da molti libri di testo, risulta alla fine
impervia, perché non è affatto chiaro come possano essere definite la somma,
il prodotto ed il quoziente di decimali infiniti non periodici. Nel caso di
decimali finiti o periodici lo sappiamo fare riducendoli prima a quozienti di
due interi. In mancanza di questa possibilità di riduzione anche la definizione
della somma di due decimali infiniti non periodici diviene difficile.
Noi, come il libro di testo, prenderemo un’altra strada, e cioè la strada
della definizione assiomatica dei numeri reali.
Definire assiomaticamente un oggetto matematico significa elencare le
proprietà che si vuole che questo oggetto abbia e quindi definire l’oggetto come quella cosa (se esiste) che soddisfa a queste proprietà. Sono pro-
4
prio queste proprietà, che vengono chiamate assiomi, a definire l’oggetto in
questione.
Un esempio elementare di definizione assiomatica è fornito dalla definizione
di un pezzo del gioco degli scacchi. Si definisce, ad esempio, il re, come il
pezzo che può muoversi in ogni direzione di un solo passo. Sono le regole del
gioco a definire re, regina, alfiere, cavallo, torre e pedone, e non la particolare
forma che i pezzi possono avere.
Le definizioni assiomatiche hanno però un limite, quello che le proprietà
indicate come assiomi non devono essere contraddittorie. Quando si introduce per via assiomatica un concetto nuovo in matematica, bisognerebbe
accertarsi che non si sono introdotte proprietà contraddittorie.
Uso il condizionale perché noi introdurremo per via assiomatica i numeri
reali, ma non faremo l’ulteriore passo di dimostrare, che questi assiomi non
introducono contraddizioni. Questo passo ulteriore può essere fatto, ma non
è un argomento che può essere affrontato in un insegnamento del primo anno
diretto ad allievi ingegneri. Mi limiterò a fornire una indicazione bibliografica. Gli interessati potranno consultare il libro di Walter Rudin ”Principi
di Analisi Matematica”, McGraw-Hill Libri Italia, 1991, ed in particolare
l’appendice al Capitolo I.
Ecco quindi la definizione assiomatica dei numeri reali.
I numeri reali, indicati con R sono un insieme nel quale sono definite due
operazioni: la somma indicata come x + y ed il prodotto, indicato con x · y,
ed una relazione indicata con x < y, che soddisfano alle seguenti proprietà
ASSIOMI ALGEBRICI.
a) Proprietà associativa.
Per ogni x, y, z ∈ R,
(x + y) + z = x + (y + z),
x · (y · z) = (x · y) · z.
b) Proprietà commutativa
Per ogni x, y ∈ R,
x + y = y + x,
x · y = y · x.
c) Proprietà distributiva
Per ogni x, y, z ∈ R,
x · (y + z) = x · y + x · z
d) Esistenza dello zero
0.1. NUMERI REALI
5
Esiste un elemento 0 tale che, per ogni x ∈ R,
x + 0 = x.
e) Esistenza dell’unità
Esiste un elemento 1 tale che, per ogni x ∈ R,
1 · x = x.
f) Esistenza dell’opposto.
Per ogni x ∈ R esiste un elemento −x tale che
−x + x = 0.
g) Esistenza dell’inverso.
Per ogni x 6= 0 esiste un elemento x−1 tale che
x · x−1 = 1.
ASSIOMI DELL’ORDINE
E’ definita in R una relazione x < y che soddisfa alle seguenti proprietà
a) Proprietà transitiva
Se x < y e y < z allora x < y
b) Proprietà di tricotomia
Se x, y ∈ R allora si verifica una ad una sola delle seguenti tre relazioni:
x = y, x < y, y < x.
ASSIOMI DI COLLEGAMENTO TRA OPERAZIONI E ORDINE
a) Se x < y allora per ogni z ∈ R x + z < y + z.
b) Se x < y e 0 < z, allora x · z < y · z.
Osserviamo che tutti gli assiomi finora elencati sono soddistatti dai numeri razionali Q con le operazioni di somma e prodotto e la relazione di
ordine ben definite in questo insieme. Sarà necessario quindi aggiungere un
altro assioma per ottenere un sistema più ampio.
Prima di enunciare questo assioma dobbiamo introdurre (come fa il libro
di testo) il concetto di insieme limitato e di maggiorante.
Introduciamo prima una notazione particolarmente comoda. Diremo che
x ≤ y se x < y o x = y. Dire che x ≤ y equivale quindi a dire che non è vero
che x < y. Similmente introduciamo la notazione x ≥ y per significare che
non è vero che x < y.
Supponiamo di avere un sistema che soddisfa agli assiomi già enunciati.
Diremo che un elemento M è un maggiorante di un insieme E se per ogni elemento x ∈ E si verifica che x ≤ M . Un insieme che ammette un maggiorante
si dice superiormente limitato
6
Esercizio 4 Definire che cosa si intende per minorante di un insieme e
definire che cosa si intende per insieme inferiormente limitato.
ASSIOMA DI COMPLETEZZA
Se E è un insieme non vuoto superiormente limitato allora esiste un
elemento sup E che è il più piccolo dei suoi maggioranti.
Possiamo ora definire il sistema R dei numeri reali come un insieme dotato
di operazioni di somma e prodotto che soddisfano agli assiomi algebrici sopra
elencati, sul quale è definita una relazione di ordine che soddisfa agli assiomi
sopra elencati e che infine soddisfa all’assioma di completezza.
Possiamo ora osservare che R contiene i numeri razionali, o meglio contiene un sottoinsieme ”isomorfo” ai numeri razionali.
Partiamo dagli elementi 0 e 1 la cui esistenza ci è assicurata dagli assiomi
e consideriamo tutti gli elementi di R ottenibili attraverso somme, prodotti,
opposti e inversi (quando leciti) a partire da questi elementi. Otteniamo
quindi con le somme e gli opposti un insieme che possiamo dire isomorfo ai
numeri interi Z e considerando i quozienti (se leciti) un insieme isomorfo ai
numeri razionali Q.
Esercizio 5 Dimostrare che esiste un sottoinsieme dei numeri razionali limitato superiormente che però non possiede nei razionali un estremo superiore
(minimo dei maggioranti). Suggerimento: considerare l’insieme E = {x ∈
Q : x2 < 2}.
Esercizio 6 Dimostrare che se x ∈ R allora
x = sup{q ∈ Q : q ≤ x}.
Esercizio 7 Dimostrare che per ogni numero
√reale non negativo x ≥ 0 esiste
uno ed un solo
numero
reale
non
negativo
x (detto la radice quadrata di
√ 2
x,) tale che ( x) = x.
Esercizio 8 Trovare sottoinsiemi dei numeri reali E che soddisfino alle seguenti proprietà
1) E è limitato superiormente, ma non inferiormente
2) E è limitato inferiormente ma non superiormente
3) E è limitato superiormente ma non ha un massimo elemento.
Esercizio 9 Trovare massimi e minimi, se esistono, estremi inferiori e superiori (se esistono) di un intervallo di estremi a e b e cioè degli intervalli
[a, b], (a, b], (a, b), [a, b).
0.1. NUMERI REALI
7
Esercizio 10 Dimostrare che l’insieme dei numeri naturali considerato come
sottoinsieme dei numeri reali non è limitato.
Esercizio 11 Dimostrare che tra due numeri reali x < y esiste un numero
razionale r tale che x < r < y
Esercizio 12 Dimostrare che se x è un numero reale tale che 0 ≤ x e tale
che per ogni numero reale ε positivo risulta x < ε, allora x = 0.
Ricordiamo che il valore assoluto o modulo di x ∈ R, indicato con |x| si può
definire in diversi modi equivalenti:
1. |x| = x, se x ≥ 0, e |x| = −x se x < 0,
2. |x| = max{x, −x} è il più grande dei due numeri x e −x,
3. |x| è la distanza tra x e 0 sulla retta reale.
Esercizio 13 Dimostrare che le tre precedenti definizioni sono equivalenti
Esercizio 14 Dimostrare che
|x + y| ≤ |x| + |y|,
|x · y| = |x| · |y|.
Esercizio 15 Dimostrare, utilizzando il precedente esercizio che
||x| − |y|| ≤ |x − y| ≤ |x| + |y|.
Esercizio 16 Dimostrare che
√
x2 = |x|,
Esercizio 17 Dimostrare che
|xn | = |x|n ,
per ogni numero intero n. (Se n è negativo si deve però supporre x 6= 0.)
Esercizio 18 Osservare che la distanza tra due numeri, x ed y nella retta
reale è data da |x − y|. Disegnare quindi sulla retta reale gli insiemi seguenti, stabilire se sono limitati inferiormente e/o superiormente e calcolare gli
eventuali estremi superiori e inferiori, massimi e minimi.
8
1. {x : |x| ≤ 1},
2. {x : |x| < 1}
3. {x : |x| ≥ 1}
4. {x : |x| > 1}
5. {x : |x − 2| ≤ 1},
6. {x : |x − 1| < 1}
7. {x : |x + 1| ≥ 1}
8. {x : |x + 2| > 1}
9. {x : |x − 1| < |x + 2|}
10. {x : |x − 2| ≥ |x + 1|}
11. {x : |x| > |x + 2|}