Trigonometria I
In questa prima parte della trigonometria deniamo le funzioni trigonometriche seno, coseno e
tangente e le loro funzioni inverse. Vedremo anche come utilizzarle nella risoluzione dei triangoli.
Cominciamo però con la denizione di un' unità di misura per gli angoli; il radiante.
A ngoli
Il sistema internazionale per le unità di misura ( S. I. ) prevede l' uso del radiante ( rad) come unità
di misura degli angoli piani. Vediamo allora quale è la denizione di questa unità di misura e
come passare dai gradi ai radianti o viceversa.
Il radiante è denito come la misura dell' angolo al centro di una circonferenza che sottende un
arco di lunghezza pari al raggio della circonferenza.
La comodità del radiante sta nella relazione semplice tra la misura dell' angolo e la lunghezza
dell' arco sotteso; moltiplicando l' angolo per il raggio otteniamo la lunghezza dell' arco. In un cerchio di raggio unitario, la misura di un' angolo al centro corrisponde alla misura dell' arco sotteso.
Se un angolo è espresso in gradi e lo vogliamo trasformare in radianti, lo moltiplichiamo per
Se un angolo è espresso in radianti e lo vogliamo trasformare in gradi, lo moltiplichiamo per
1 80
1 80
Quando usiamo le calcolatrici elettroniche dobbiamo prestare attenzione all' unità di misura in
uso. Infatti queste calcolatrici possono lavorare con i radianti ( rad) , con i gradi sessadecimali
( deg, l' angolo retto vale 90 deg) e i gradi centesimali ( grad, l' angolo retto vale 1 00 grad) .
trigonometria I pag. 1
Deniamo ora le funzioni trigonometriche
gradi, grazie ad un triangolo rettangolo.
sin , co s
e
tan ,
sa
per degli angoli compresi tra 0 e 90
cateto
opposto
ad α
u
en
t
po
i
α
cateto adiacente ad α
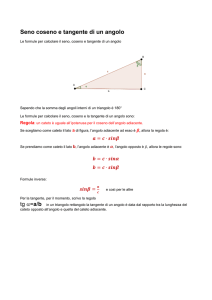
seno dell'angolo , notato sin , è il rapporto tra il cateto opposto ad e l' ipotenusa.
(
)
cateto opposto ad α
sin(α)=
ipotenusa
coseno di , notato cos , è il rapporto tra il cateto adiacente ad e l' ipotenusa.
(
)
cos(α)=
cateto adiacente ad α
ipotenusa
tangente di , notata tan , è il rapporto tra il cateto opposto e il cateto adiacente ad .
( la tangente non è denita per un angolo di 90 °) .
(
)
tan(α)=
cateto opposto ad α
cateto adiacente ad α
Relazioni fondamentali
Dalle denizioni precedenti deduciamo che il rapporto tra sin e cos corrisponde a tan ;
(
tan (
) =
sin cos (
)
(
)
)
(
)
(
)
Il teorema di Pitagora ci conduce alla seconda relazione fondamentale della trigonometria;
( il quadrato di sin è notato sin )
(
)
2
(
)
sin 2
(
) +
cos 2
(
) = 1
trigonometria I pag. 2
funzioni inverse
Abbiamo denito la funzione sin per degli angoli compresi tra 0 e 90 gradi; ad ogni angolo corrisponde un numero compreso tra 0 e 1 . La funzione così denita è biunivoca e quindi invertibile.
sin
angoli
da 0 a 90
gradi
0
0
30
45
numeri
da 0 a 1
o
o
0.5
o
0.7071
90
o
1
La funzione inversa è chiamata arc sin o anche sin ?
1
sin -1
angoli
da 0 a 90
gradi
0
30
45
numeri
da 0 a 1
o
0
o
0.5
o
90
0.7071
o
1
Ciò signica che se conosciamo il valore del seno di un angolo, possiamo risalire al valore
dell' angolo. Se di un triangolo rettangolo conosciamo l' ipotenusa, per es. 5 cm, e un cateto, per
es. 4 cm, sappiamo che il seno dell' angolo opposto al cateto di 4 cm vale 4/5 e, interrogando la
calcolatrice scopriamo che quell' angolo vale sin ?
53. 1 3 °.
1
( 4/ 5 ) =
Abbiamo le funzioni inverse anche per co s e tan ; le chiamiamo arcco s o cos ? e arctan o tan ?
1
cos -1
angoli
da 0 a 90
gradi
0
numeri
da 0 a 1
o
tan -1
angoli
da 0 a 90 gradi
(90 escluso)
0
30
numeri
da 0
a infinito
o
1
0
o
45
o
0.866
45
o
0.7071
90
o
1
60
o
1.732
89
0
1
o
57.29
trigonometria I pag. 3
risoluzione di triangoli rettangoli
Di un triangolo possiamo conoscere la misura dei lati e desiderare conoscere il valore dei suoi
angoli. Oppure conoscere la lunghezza di due lati e la misura di un angolo e voler determinare la
lunghezza del terzo lato e la misura degli altri angoli. Per risoluzione di triangoli intendiamo
proprio questo; la determinazione delle misure che ancora non conosciamo a partire da quello
che già sappiamo. Per la risoluzione dei triangoli rettangoli faremo uso del teorema di pitagora e
di quanto abbiamo appreso sulle funzioni trigonometriche sin, cos, tan e le loro inverse.
conosciuti
troviamo
ipo
ipotenusa * sin(α)
ten
usa
ipo
ten
usa
α
α
ipotenusa * cos(α)
cateto adiacente ad α * tan(α)
cateto adiacente ad α / cos(α)
α
α
α
cateto adiacente ad α
cateto opposto
ad α
cateto opposto
ad α
cateto adiacente ad α
cateto opposto ad α / sin(α)
α
cateto opposto ad α / tan(α)
cateto a
cateto a
pitagora
cateto b
arctan(cateto a / cateto b)
cateto b
arccos(cateto a / ipotenusa)
ipo
ten
usa
cateto a
cateto a
ipo
ten
usa
arcsin(cateto a / ipotenusa)
pitagora
trigonometria I pag. 4
Se vogliamo occuparci di triangoli qualsiasi dovremo considerare degli angoli tra 0 e 1 80 °.
Avremo dunque bisogno di estendere la denizione di seno e coseno n qui data. Per ora però
anticipiamo solo che due angoli supplementari ( la loro somma da 1 80 °) hanno lo stesso seno
mentre il loro coseno è uguale in valore assoluto ma di segno opposto. In formule avremo:
sin sin 1 80 ° ? cos ? cos 1 80 ° ? (
(
) =
) =
(
)
(
)
teorema dei seni ( Eulero)
Dalla geometria sappiamo che tutti gli angoli alla circonferenza che si appoggiano ad una corda
data sono uguali o supplementari. Il rapporto tra la lunghezza della corda e il diametro della
circonferenza dipende unicamente dal valore dell' angolo e corrisponde al seno dell' angolo.
Dato un qualsiasi triangolo, possiamo sempre disegnare una circonferenza che passa per i suoi
vertici. È la circonferenza circoscritta.
Il seno di un' angolo del triangolo sarà equivalente al rapporto tra il lato opposto all' angolo e il
diametro della circonferenza. Per d diametro della circonferenza circoscritta avremo:
sin =
a
d
sin =
b
d
sin =
c
d
Isolando il diametro in ognuna delle eguaglianze precedenti otteniamo precisamente il teorema
dei seni:
d=
a
sin =
b
c
sin sin =
trigonometria I pag. 5
teorema del coseno ( Carnot)
Il teorema del coseno assomiglia a quello di Pitagora ma vale per tutti i triangoli. E dice che:
a 2 = b 2 + c 2 ? 2 b c cos Per convincercene disegnamo l' altezza z , relativa al lato b e deniamo x c cos e y b ? x .
=
=
Usando Pitagora e la denizione di y avremo:
8
><
>:
Per sostituzione otteniamo a
2
=
a2 = z 2 + y2
z 2 = c2 ? x 2
y2 = b2 + x 2 ? 2 b x
b 2 + c 2 ? 2 b x e ricordando che x = c cos abbiamo il teorema.
Esercizi
a) scrivere il teorema per gli altri lati:
b2 =
c2 =
b) girare la formula isolando l' angolo:
=
=
=
trigonometria I pag. 6
Risoluzione di triangoli qualsiasi
Qui di seguito illustriamo quello che potrebbe essere il primo passo nella risoluzione di un triangolo qualsiasi. Facciamo uso dei teoremi di Eulero e di Carnot e ricordiamo che la somma degli
angoli di un triangolo vale 1 80 °.
dati
troviamo
due lati e l’angolo compreso
c
c
α
α
(Carnot)
b
b
tutti i lati
c
a
c
a
α
(Carnot)
b
b
un lato e gli angoli
β
β
γ
α
γ
(Eulero)
α
b
b
le lunghezze di due lati e l’ampiezza di un angolo non compreso
(ci possono essere zero, una o due soluzioni)
a
a
a
α
b
a
α
(Eulero)
b
trigonometria I pag. 7
Estendiamo ora la denizione della funzione seno ad angoli qualsiasi. Utilizziamo per questo una
circonferenza di raggio unitario centrata all' origine degli assi cartesiani. In questa circonferenza
disegnamo degli angoli orientati che originano dal semiasse x positivo e hanno valore positivo se
il loro verso è antiorario ( vedi gura sotto) .
Dalla denizione precedente sappiamo che per gli angoli da 0 a 90 gradi il seno di corrisponde
alla coordinata y del punto P . Estendiamo allora la denizione di seno dicendo che questo vale
per qualsiasi angolo.
La funzione così denita trasforma un angolo qualsiasi in un numero compreso tra ? e
.
1
+ 1
Nel graco sopra gli angoli sono espressi in gradi mentre sotto sono radianti.
trigonometria I pag. 8
Per estendere la denizione di coseno ad angoli qualsiasi utilizziamo di nuovo la circonferenza di
raggio unitario; il coseno di corrisponde alla coordinata x del punto P .
Così il punto P che si muove sulla circonferenza unitaria avrà coordinate x P yP
(
;
) = (
cos sin ;
)
Il graco della funzione co s sarà uguale a quello della funzione sin salvo uno sfasamento di 90 °.
Queste due funzioni sono
scrivere:
pe riodic he
e il loro periodo è di 360 ° ( radianti) . Per k 2 Z possiamo
2
sin (
cos (
) =
) =
sin k 360 °
(
+
)
cos k 360 °
(
+
)
Inoltre possiamo vericare che valgono le seguenti identità:
sin (
) =
cos (
sin 1 80 ° ? ) =
(
cos ? (
)
)
trigonometria I pag. 9
Nella gura seguente sono riportate le coordinate di alcuni punti particolari sulla circonferenza
unitaria. Gli angoli che li caratterizzano sono dati sia in gradi che in radianti.
Nel primo quadrante sia il seno che il coseno sono positivi ( o nulli) , nel secondo quadrante il
seno è positivo e il coseno negativo, nel terzo quadrante entrambe le funzioni sono negative
mentre nel quarto quadrante il seno è negativo e il coseno positivo.
trigonometria I pag. 1 0