SECONDA LEZIONE – tre applicazioni del teorema di Talete
I due pilastri della geometria euclidea sono i teoremi di Pitagora e di Talete.
Riprendiamo Talete:
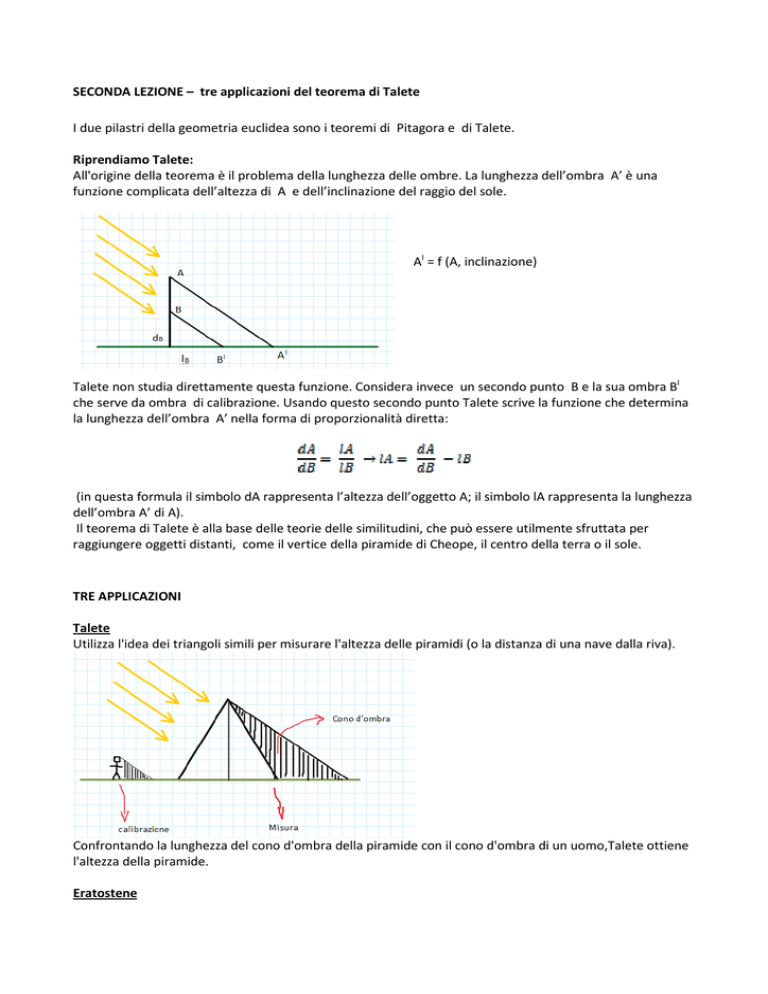
All'origine della teorema è il problema della lunghezza delle ombre. La lunghezza dell’ombra A’ è una
funzione complicata dell’altezza di A e dell’inclinazione del raggio del sole.
AI = f (A, inclinazione)
Talete non studia direttamente questa funzione. Considera invece un secondo punto B e la sua ombra BI
che serve da ombra di calibrazione. Usando questo secondo punto Talete scrive la funzione che determina
la lunghezza dell’ombra A’ nella forma di proporzionalità diretta:
(in questa formula il simbolo dA rappresenta l’altezza dell’oggetto A; il simbolo lA rappresenta la lunghezza
dell’ombra A’ di A).
Il teorema di Talete è alla base delle teorie delle similitudini, che può essere utilmente sfruttata per
raggiungere oggetti distanti, come il vertice della piramide di Cheope, il centro della terra o il sole.
TRE APPLICAZIONI
Talete
Utilizza l'idea dei triangoli simili per misurare l'altezza delle piramidi (o la distanza di una nave dalla riva).
Confrontando la lunghezza del cono d'ombra della piramide con il cono d'ombra di un uomo,Talete ottiene
l'altezza della piramide.
Eratostene
A causa del moto annuale, l'altezza del sole sul piano dell'equatore cambia di giorno in giorno. All'equinozio
è esattamente sull'equatore; ai solstizi si trova sopra ai tropici ( del cancro a Nord, d'estate; del capricorno
a Sud, d'inverno).
La conseguenza è la variazione periodica dell'inclinazione dei raggi solari.
Considerando il solstizio di estate:
Ad Assuan (a Sud di Alessandria) il sole è alla
verticale a mezzogiorno: l'ombra proiettata da
un bastone cade al piede del bastone.
Spostiamoci alla stessa ora ad Alessandria, che
si trova sullo stesso meridiano ad una distanza s
da Assuan più a Nord.
Poiché Alessandria è più a Nord, il sole non è
sulla verticale locale e quindi un bastone
proietta l'ombra.
Misurando l'ombra del bastone sto misurando l'angolo al
entro che separa Assuan da Alessandria.
Allora:
In questo modo Eratostene ha misurato il raggio della terra senza mai muoversi da Alessandria.
Aristarco di Samo
L'unica opera rimasta è quella sulle dimensioni della luna e del sole e la loro distanza dalla terra.
Cambiando cono d'ombra Aristarco è arrivato a stimare la dimensione Ds (diametro) del sole. La sua idea è
di considerare il cono d'ombra proiettato dalla terra durante un’ eclisse di luna. Usando la luna per
calibrare il cono d'ombra della terra, alla maniera di Talete, Aristarco è arrivato a stimare che il rapporto tra
il diametro Ds del sole e il diametro Dt della terra non fosse inferiore a 19/3 e non potesse essere
superiore a 43/6 .
In questo modo Aristarco, stando sempre
sulla terra è riuscito a stimare il diametro del
sole.
EUCLIDE:
Ritorniamo al teorema di Pitagora con lo scopo di chiarire la lunga strada che porta alla sua dimostrazione.
Quelle date in precedenza non possono essere considerate vere dimostrazioni, semmai delle verifiche
sperimentali, perché fanno uso di proprietà indimostrate di triangoli e quadrati.
La prima dimostrazione rigorosa del teorema di Pitagora è data da Euclide alla fine del Libo I degli Elementi
di Geometria, dopo 46 proposizioni preliminari. Nelle prossime due lezioni, ci proponiamo di esaminare la
struttura logica di questo libro, che è il fondamento teorico della Geometria.
Questo libro parla della costruzione dei triangoli, della loro uguaglianza e delle relazioni di uguaglianza e di
diseguaglianza che intercorrono tra i lati e gli angoli di un triangolo. Ogni triangolo possiede 3 lati e 3 angoli.
L'esperienza più elementare mostra che questi dati sono legati tra di loro.
Si pongono subito alcuni problemi:
1.
Quanti elementi servono a definire in triangolo?
2.
Quale arbitrarietà c’è nella scelta di questi elementi?
3.
Che relazioni intercorrono fra i lati e gli angoli di un triangolo?
A queste domande dà risposta il primo libro degli Elementi di Euclide.
Come si colloca il teorema di Pitagora all'interno di questa problematica? Per vederlo partiamo dal primo
criterio di uguaglianza (che possiamo accettare come un assioma di base della teoria) secondo cui due lati e
l'angolo compreso determinano univocamente il triangolo. Ciò significa che il terzo lato C del triangolo è
una funzione nota degli altri tre elementi.
In notazione moderna scriviamo: c = f (a, b, α)
Il teorema di Pitagora specifica questa funzione nel caso particolare in cui
( caso a cui ci si può sempre ridurre decomponendo opportunamente il
triangolo dato in triangoli rettangoli) . La risposta è
Mentre in Talete la funzione che determina la lunghezza dell’ombra, nota
l’altezza dell’ oggetto, era lineare (similitudine), in Pitagora la funzione che
determina il terzo lato è quadratica. Dal punto di vista dei geometri greci l'unico modo di rappresentare il
prodotto di due segmenti è di interpretarlo come un rettangolo. Pertanto l’unico modo che i geometri greci
avevano per rappresentare una funzione quadratica era di interpretarla come relazione tra le aree di
opportuni rettangoli. Da qui la forma usuale dell’enunciato del teorema di Pitagora, e la lunga strada
necessaria per arrivare alla sua dimostrazione. Essa passa attraverso lo studio dell’equivalenza delle aree
dei parallelogrammi.












