TEOREMA DI TALETE
Piccolo Teorema di Talete
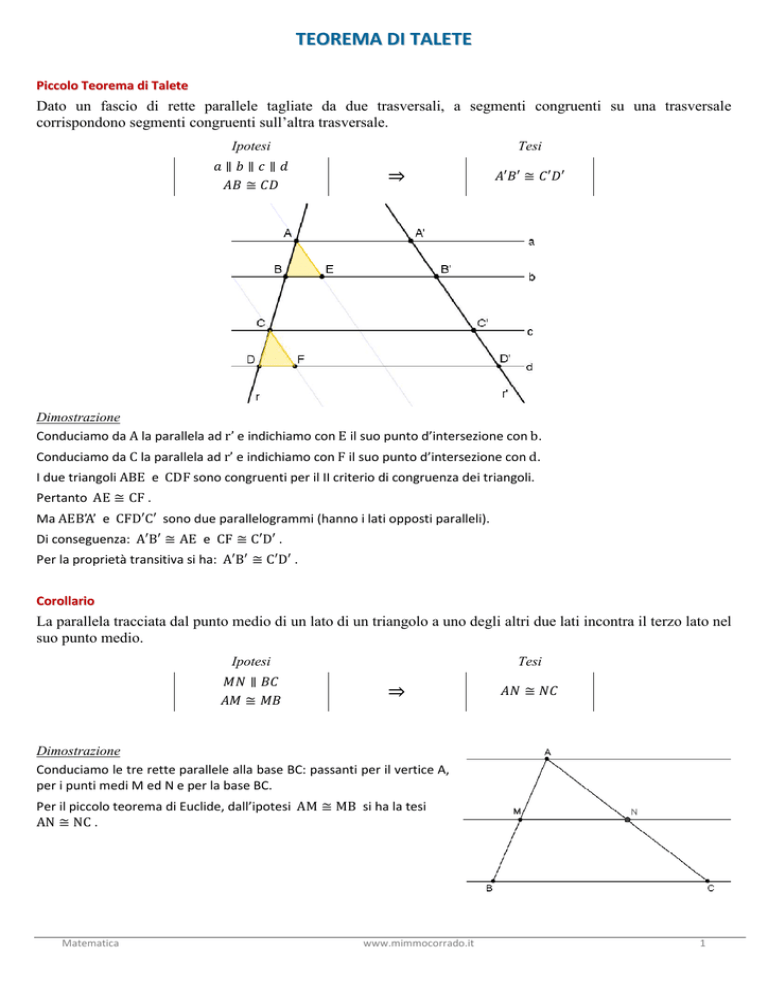
Dato un fascio di rette parallele tagliate da due trasversali, a segmenti congruenti su una trasversale
corrispondono segmenti congruenti sull’altra trasversale.
Ipotesi
∥∥∥
≅ Tesi
⇒
′′ ≅ ′
′
Dimostrazione
Conduciamo da A la parallela ad r’ e indichiamo con E il suo punto d’intersezione con b.
Conduciamo da C la parallela ad r’ e indichiamo con F il suo punto d’intersezione con d.
I due triangoli ABE e CDF sono congruenti per il II criterio di congruenza dei triangoli.
Pertanto AE ≅ CF .
Ma AEB’A’ e CFD′C′ sono due parallelogrammi (hanno i lati opposti paralleli).
Di conseguenza: A′B′ ≅ AE e CF ≅ C′D′ .
Per la proprietà transitiva si ha: A′B′ ≅ C′D′ .
Corollario
La parallela tracciata dal punto medio di un lato di un triangolo a uno degli altri due lati incontra il terzo lato nel
suo punto medio.
Ipotesi
∥ ≅ Tesi
⇒
≅ Dimostrazione
Conduciamo le tre rette parallele alla base BC: passanti per il vertice A,
per i punti medi M ed N e per la base BC.
Per il piccolo teorema di Euclide, dall’ipotesi AM ≅ MB si ha la tesi
AN ≅ NC .
Matematica
www.mimmocorrado.it
1
Teorema dei punti medi
Il segmento che congiunge i punti medi di due lati di un triangolo è parallelo al terzo lato e congruente alla sua
metà.
Ipotesi
≅ ≅ ⇒
Tesi
∥ 1
≅ 2
Dimostrazione ∥ Supponiamo per assurdo che la retta MN non sia parallela alla retta BC.
Pertanto dovrà esistere un’altra retta passante per B parallela a MN. Indichiamo con C’ il suo punto d’intersezione con la
retta AC. Perilteoremaprecedente:
≅ ′.
?????? ≅ ???? .
Confrontandotalerelazioneconquelladella
dellaipotesi: ≅ 9:;:<=>:′
Ciò vuol dire che la retta ′ ≡ e quindi la retta BC risulterebbe parallela alla retta MN , contro quanto supposto.
-
Dimostrazione ≅ . Conduciamo da M la parallela al lato BC.. Per il corollario precedente questa
parallela incontra il lato AC nel suo punto
nto medio N.
Conduciamo da N la parallela al lato AB.. Per il corollario precedente questa
parallela incontra il lato BC nel suo punto medio D.
-
Pertanto si ha che: BD ≅ . BC.
Il quadrilatero MNDB, avendo i lati opposti paralleli,
paralleli è un parallelogramma.
Quindi MN ≅ BD .
.
Per la proprietà transitiva si ha: MN ≅ BC.
BC
Grandezze commensurabili e incommensurabili
Due grandezze omogenee sono commensurabili se esiste una grandezza,, omogenea con le due date, che sia loro
sottomultiplo comune. In altro modo si potrebbe dire: Due grandezze omogenee e sono commensurabili se e solo
/
/
se esiste un numero razionale 0 tale che 2 0 Due grandezze omogenee sono incommensurabili se non esiste una grandezza, omogenea con le due date, che sia loro
sottomultiplo comune.
Misura di una grandezza commensurabile
Date due grandezze e 1,, fra loro commensurabili, si definisce misura della grandezza rispetto alla grandezza 1, il
/
3
numero razionale tale che: 2 1.. La misura della grandezza è indicata con ̅.
0
4
La grandezza U è detta unità di misura. L’unità di misura della lunghezza è il metro.
Matematica
www.mimmocorrado.it
2
Misura di una grandezza incommensurabile
È possibile estendere il concetto di misura anche a grandezze incommensurabili, purché si utilizzino i numeri reali
anziché i numeri razionali. La misura di una grandezza A incommensurabile rispetto ad una grandezza U è un numero
irrazionale.
Teorema
La diagonale di un quadrato e il suo lato sono segmenti incommensurabili.
Dimostrazione
Applicando il T. di Pitagora si ha:
d 2 √l. B l. 2 √2l. 2 √2l
(*) La dimostrazione che √2
Matematica
ma √2 non è un numero razionale C∗E.
non è un numero razionale è svolta nella dispensa sui radicali.
www.mimmocorrado.it
3
Teorema di Talete
Il piccolo teorema di Talete visto precedentemente può essere così riformulato:
Dato un fascio di rette parallele tagliate da due trasversali, se due segmenti AB e CD su una trasversale hanno
rapporto 1 (che equivale a dire che sono congruenti), anche i segmenti A’B’ e C’D’ sulla seconda trasversale
FG
F’G’
hanno rapporto uguale a 1, quindi:
=
.
HI
H’I’
Ora generalizziamo questo risultato, dimostrando che l’uguaglianza tra questi rapporti sussiste anche se i segmenti e
non sono tra loro congruenti.
Grande Teorema di Talete
Dato un fascio di rette parallele tagliate da due trasversali, il rapporto tra due segmenti e individuati dal
fascio su una trasversale è uguale al rapporto tra i loro corrispondenti ’’ e ’
’ sull’altra trasversale.
Ipotesi
∥∥∥
e ′
′ sono i
corrispondenti di e J J
Tesi
⇒
???? ??????
′′
=
????
??????
′
′
Dimostrazione
Per semplificare, consideriamo il caso in cui i segmenti e siano commensurabili (si può dimostrare però che il teorema
è valido anche nel caso in cui i segmenti e sono incommensurabili).
3
Sia pertanto:
=
con 3 e 4 numeri naturali.
4
Ciò significa che esiste un segmentino K tale che ≅ 3K e ≅ 4K.
Consideriamo:
I punti che dividono il segmento in 3 segmentini congruenti ad K (nel nostro grafico 3 = 3);
I punti che dividono il segmento in 4 segmentini congruenti ad K (nel nostro grafico 4 = 2).
Tracciamo da tali punti le rette parallele alle altre rette del fascio.
I punti di intersezione di tali rette con la trasversale ; J suddividono ′′ e ′
′ , rispettivamente, in 3 segmentini e in 4
segmentini. Questi segmentini, per il piccolo Teorema di Talete, sono tutti congruenti ad K. Si ha allora:
J J 3K 3
J J J J
J J
≅ 4K
⇒
=
=
⇒
=
.
≅ 3K >
J J 4K 4
J J Matematica
www.mimmocorrado.it
4
Conseguenze del Teorema di Talete
Retta parallela ad un lato del triangolo
Se una retta parallela a un lato di un triangolo interseca gli altri due lati, li divide in segmenti proporzionali.
Ipotesi
Tesi
; ∥ M ∩ = OPQ
M ∩ = ORQ
???? R
????
P
=
????
P ????
R
⇒
Dimostrazione
Tracciamo la retta 9, passante per e parallela al lato .
Otteniamo così tre rette parallele ;, 9 e tagliate dalle trasversali ed .
Pertanto, per il teorema di Talete, risulta:
P AQ
=
PB QC
Teorema inverso - Retta parallela ad un lato del triangolo
Se una retta interseca due lati di un triangolo in segmenti proporzionali sui due lati, allora la retta è parallela al
terzo lato.
Ipotesi
???? R
????
P
=
????
????
P R
M ∩ = OPQ
M ∩ = ORQ
Tesi
⇒
PR ∥ Dimostrazione per assurdo
Supponiamo per assurdo che la retta PQ non sia parallela alla retta BC.
Pertanto dovrà esistere un’altra retta passante per B parallela a PQ . Indichiamo con C’ il suo punto d’intersezione con la
retta AC.
Matematica
www.mimmocorrado.it
5
Per il teorema precedente sarà valida la seguente proporzione:
????
????
P R
=
.
P ?????
R′
????
???? R
P
?????J .
???? ≅ R
=
9: ;:< ℎ>: R
????
????
P R
Ciò vuol dire che la retta ≡ ’ e quindi la retta BC risulterebbe parallela alla retta PQ , contro quanto supposto.
Confrontando tale relazione con quella della ipotesi:
Teorema della bisettrice
In un triangolo, la bisettrice di un angolo interno divide il lato opposto in segmenti proporzionali agli altri due
lati.
Ipotesi
W
≅ W
⇒
Tesi
???? ????
=
????
????
Dimostrazione
Tracciamo da la retta parallela alla bisettrice e indichiamo con X il suo
punto d’intersezione con il prolungamento del lato .
Y ≅ Z perché angoli corrispondenti rispetto alle rette parallele e X
tagliate dalla trasversale .
Z ≅ [ per ipotesi.
[≅\
perché angoli alterni interni rispetto alle rette parallele e X
tagliate dalla trasversale .
Per la proprietà transitiva si ha: Y ≅ \.
Pertanto il triangolo X è isoscele sulla base X, ossia ≅ X.
Per il teorema della “Retta parallela ad un lato del triangolo” si conclude che:
???? ????
=
????
????
Matematica
www.mimmocorrado.it
6
LA SIMILITUDINE
Omotetie
Una omotetia di centro ] e rapporto ^ C^ ∈ ME, è una corrispondenza biunivoca tra punti del piano che lascia fisso il
punto ] e trasforma ogni altro punto P del piano, diverso da ], nel punto P′ tale che:
Se ^ > 0 P′ appartiene alla semiretta ]P
Se ^ < 0 P′ appartiene alla semiretta opposta ad ]P
]P′ ≅ |^|]P
^>0
^<0
Proprietà
Una omotetia trasforma:
Una retta in un’altra retta a essa parallela
Un segmento in un segmento parallelo al primo e tale che il rapporto è uguale al valore assoluto del rapporto di
omotetia
Un angolo in un angolo a esso congruente.
Similitudine
Una similitudine è una trasformazione ottenuta dalla
composizione di una omotetia e di una isometria, o viceversa.
Due figure si dicono simili se si corrispondono in una
similitudine.
Per indicare che il poligono d è simile al poligono d’ si utilizza la
seguente scrittura e ≈ e′.
Due lati o due angoli che si corrispondono in una similitudine si
dicono omologhi.
La similitudine gode di tutte le proprietà delle omotetie.
In particolare:
Se due poligoni sono simili, hanno gli angoli omologhi
congruenti e i lati omologhi in proporzione.
Il rapporto fra due lati omologhi si chiama rapporto di
similitudine.
Matematica
www.mimmocorrado.it
7
Primo criterio di similitudine dei triangoli
Se due triangoli hanno due angoli ordinatamente congruenti, allora sono simili.
Secondo criterio di similitudine dei triangoli
Se due triangoli hanno due lati ordinatamente in proporzione e l’angolo fra essi compreso congruente, allora sono simili.
Secondo criterio di similitudine dei triangoli
Se due triangoli hanno i lati ordinatamente in proporzione, allora sono simili.
Teorema – Proporzionalità fra gli elementi dei triangoli
In due triangoli simili, di rapporto di similitudine ^:
il rapporto tra le misure di due altezze omologhe è uguale al rapporto di similitudine
il rapporto tra i perimetri è uguale al rapporto di similitudine
/
/J
g
gh
2^
2^
il rapporto tra le aree è uguale al quadrato del rapporto di similitudine
i
ih
2 ^..
Teorema delle corde
Se in una circonferenza due corde si intersecano, i segmenti che si formano sulla
prima corda e quelli che si formano sulla seconda corda, rispettivamente, sono i
medi e gli estremi di una stessa proporzione.
P ∶ P = P
∶ P
Dimostrazione
P
≈ P
per il I° Criterio di similitudine.
Infatti:
L’angolo PW
≅ PW perché opposti al vertice
k ≅ W perché angoli alla circonferenza che insistono sullo stesso arco AC
Pertanto i lati omologhi dei due triangoli sono in proporzione: P ∶ P = P
∶ P .
Teorema delle secanti
Se da un punto P esterno ad una circonferenza si conducono due secanti e si
considerano i segmenti che hanno un estremo in P e l’altro in ciascuno dei
punti di intersezione, i segmenti sulla prima secante sono gli estremi e i
segmenti sulla seconda secante sono i medi di una stessa proporzione.
P ∶ P = P ∶ P
Dimostrazione
P
≈ P
per il I° Criterio di similitudine.
Infatti:
L’angolo PW è in comune
k ≅ W perché angoli alla circonferenza che insistono sullo stesso arco AC
P
Pertanto i lati omologhi dei due triangoli sono in proporzione: P ∶ P = P ∶ P
.
Matematica
www.mimmocorrado.it
8
Teorema della tangente
Se da un punto P esterno ad una circonferenza si conducono una secante e
una tangente, il segmento di tangente che ha per estremi il punto P e il punto
di tangenza è medio proporzionale fra i segmenti di secante che hanno per
estemi il punto P e ciascuno dei punti di intersezione.
P ∶ Pl = Pl ∶ P
Dimostrazione
Pl ≈ Pl
per il I° Criterio di similitudine.
Infatti:
L’angolo PW è in comune
k ≅ W perché angoli alla circonferenza che insistono sullo stesso arco AT
P
Pertanto i lati omologhi dei due triangoli sono in proporzione:
P ∶ P = P ∶ P
.
Criterio di similitudine dei poligoni
Due poligoni aventi lo stesso numero dei lati sono simili se:
a. hanno gli angoli ordinatamente congruenti
b. il rapporto fra le misure dei lati opposti agli angoli congruenti è costante.
Teorema – Perimetri e aree di poligoni simili
Se due poligoni sono simili e il loro rapporto di similitudine è ^, allora:
a. il rapporto fra i loro perimetri è uguale al rapporto di similitudine
/
/J
=^
b. il rapporto fra le loro aree è uguale al quadrato del rapporto di similitudine
i
ih
= ^. .
Teorema – Poligoni regolari e circonferenza circoscritta
I perimetri di due poligoni regolari con lo stesso numero di lati stanno fra loro come i rispettivi apotemi e come i raggi
delle rispettive circonferenze circoscritte.
3 ∶ 3J = ; ∶ ;′
Matematica
3 ∶ 3J = ∶ ′
www.mimmocorrado.it
9