I 2

1
Velocità di reazione
A
V=-
d[A]
dt
=
B
d[B]
dt
V= Velocità istantanea: coefficiente angolare della retta
tangente alla curva in quel punto
Quando t=0 la velocità istantanea sarà massima (V0)
2
Urti molecolari e velocità di reazione (1)
Teoria delle collisioni (Arrhenius, 1888)
Es: A2 + B2 → [A2B2] → 2AB
Ogni reazione chimica
Complesso attivato
B-B
A─A
B B
B
B
A
A
A
A
Energia libera, G
A A
Condizioni per un “urto efficace”:
A2B2
Ea
A2+ B2
Energia di
attivazione
BB
“Complesso attivato”
generato da un
“urto efficace”
B B
A─A
decorre attraverso la
formazione di un
2AB
Coordinata di reazione
Sufficiente energia (almeno pari a Ea)
Giusto orientamento (Effetto sterico)
B
B
A
A
3
Urti molecolari e velocità di reazione (2)
Effetto Sterico
Es1: OH- + CH3Cl 
[OH … CH3Cl]- 
Es2: N2O + NO
CH3OH + Cl-
+

[N-N…O…N-O]#

-
Sono efficaci soltanto
gli urti nei quali lo ione
ossidrile attacca
l’alogeno-derivato
alchilico dal lato
opposto a quello dove
è legato l’atomo di
alogeno
N2 + NO2
4
Urti molecolari e velocità di reazione (3)
Energia di attivazione
L’energia di attivazione (Ea) corrisponde alla minima energia
necessaria per un urto efficace
Minore è il valore di Ea maggiore è il numero di molecole in grado di
superare la barriera energetica e formare i prodotti
La reazione anche se è termodinamicamente spontanea (DGr<0)
potrebbe non avvenire se non attivata
Spontaneità di reazione non vuol dire immediatezza
C diamante  O 2g   CO 2g  DG o298  396kJ
Molto Lenta
H +aq  + OH-aq   H 2 O l  DG o298 = -79 kJ
Istantanea
5
Urti molecolari e velocità di reazione (4)
Energia di attivazione
DG° = - 115 Kcal/mol
Es: 2H2 + O2 → 2 H20
La reazione da un punto di vista
termodinamico è spontanea ma non
avviene. Occorre una scintilla che
innesca la reazione la quale poi
continuerà a fornire l’energia di
attivazione necessaria perché altre
molecole di H2 e O2 reagiscano
A A
H H
Energia libera, G
O O
HH
Ea
O-O
H-H
H-H
DGr<0
H
Coordinata di reazione
O
H
H
O
H
6
Teoria delle Collisioni e Temperatura
NE=N • e-Ea /RT
NE
N
T1 < T2 < T3
T1
Ea
T2
ECm1 ECm2
T3
Aumentando la temperatura, aumenta l’energia cinetica
media (ECm) delle molecole e di conseguenza aumenta il
n°di molecole (NE) aventi l’energia minima necessaria
per formare il complesso attivato (Ea).
Si può dimostrare (Arrhenius,1988) che a temperatura T,
la frazione di molecole che hanno energia  Ea è
proporzionale a e-E*/RT (area colorata sotto la curva)
ECm3
Energia cinetica
7
Parametri che influenzano la velocità di reazione
Secondo quanto detto sulla teoria delle collisioni è evidente che la
velocità di una reazione chimica dipende da:
Temperatura (energia cinetica)
Energia di attivazione (barriera energetica)
Fattore Sterico A (orientamento dell’urto molecolare)
k = A·e-Ea/RT
Costante cinetica
Concentrazione dei reagenti (numero degli urti)
V = k · [Concentrazione]
8
Concentrazione e velocità di reazione
aA + bB  cC + dD
V = k · [A]m · [B]n
m,n
: Ordine di reazione di un singolo reagente (si ricava solo sperimentalmente)
m + n : Ordine di reazione complessivo
Molecolarità : n° di particelle (molecole, atomi, ioni) che urtano per dar
luogo ad un singolo atto reattivo (reazione elementare)
Es1: H2 + I2  2HI
Es2: 2N2O5  4NO2 + O2
Es3: 2NO+H2  N2 + 2H2O
Es4: NO2+2HClNO+H2O+Cl2
V=k[H2][ I2]
V=k[N2O5]
V=k[NO]2[H2]
V=k[NO][HCl]
2° ordine, bimolecolare
1° ordine
3° ordine, trimolecolare
2°ordine
Solo nei processi elementari (Es1, 3) il coefficiente stechiometrico (a,b)
coincide con l’ordine di reazione (m,n) e con la molecolarità
9
Determinazione ordine di reazione (1)
A + B C
[A]
[B]
velocità
(moli/litro)
0,2
0,1
0,2
(moli/litro)
0,1
0,1
0,2
(moli/litro/minuto)
0,1
0,05
0,1
V = k·[A]
Dai dati sperimentali riportati in tabella è evidente che la reazione è
di 1° ordine, in quanto la sua velocità si dimezza quando viene
dimezzata la concentrazione di A mentre non si raddoppia quando
viene raddoppiata la concentrazione di B
10
Determinazione ordine di reazione (2)
A + B C
[A]
[B]
velocità
(moli/litro)
0,1
0,1
0,2
(moli/litro)
0,1
0,2
0,2
(moli/litro/minuto)
0,1
0,4
0,4
V = k·[B]2
Dai dati sperimentali riportati in tabella è evidente che la reazione è
di 2° ordine rispetto a B, in quanto la sua velocità è proporzionale
alla seconda potenza della concentrazione di B e non varia al variare
della concentrazione di A
11
Determinazione ordine di reazione (3)
A + B C
[A]
[B]
velocità
(moli/litro)
0,2
0,4
0,2
(moli/litro)
0,3
0,6
0,6
(moli/litro/minuto)
0,10
0,40
0,20
V = k·[A]·[B]
Dai dati sperimentali riportati in tabella è evidente che la reazione è
di 2° ordine, in quanto la sua velocità si duplica sia quando viene
raddoppiata la concentrazione di A che quando viene raddoppiata
la concentrazione di B
Si può anche dire che la reazione è di 1° ordine rispetto ad
A e di 1° ordine rispetto a B
12
Determinazione ordine di reazione (4)
In generale una reazione viene definita di 2° ordine se la sua velocità
risulta sperimentalmente essere funzione lineare della concentrazione
di un solo reagente elevata al quadrato o al prodotto delle concentrazioni
di due reagenti.
Quindi, la reazione è di secondo ordine se si verifica
sperimentalmente uno dei casi seguenti:
V = k [A]2
V = k [B]2
V = k [A][B]
13
Meccanismo di reazione
Salvo rare eccezioni l’equazione chimica rappresenta la
somma di un certo numero di reazioni intermedie
(Reazioni Elementari) da essa non desumibili
La velocità di reazione è data dallo stadio lento (tappa limitante)
Es: 2 ICl + H2  2 HCl + I2
V= k [ICl][H2]
La reazione è il risultato di due reazioni elementari
ICl + H2  HCl + HI
Stadio lento V= k [ICl][H2]
ICl + HI  HCl + I2
Stadio veloce
2 ICl + H2  2 HCl + I2
V= k [ICl][H2]
HI = “Intermedio di reazione”
14
La tappa limitante nelle reazioni a più stadi
Reagenti
Intermedi
Prodotti
Stadio 1
Stadio 2
Rapido
Lento
Stadio limitante la velocità
k
A  B  C  D FG H I
La velocità totale del processo è uguale a quella della
reazione più lenta (V= k[D])
Questo è spesso sfruttato negli organismi viventi per
regolare il metabolismo
15
L’azione del catalizzatore (1)
X + Y → X-Y
X + C → X-C
X-C + Y → X-Y + C
X + Y → X-Y
Reazione non catalizzata (Ea alta, V bassa)
Reazioni in presenza di catalizzatore (C)
(Ea bassa, V alta)
C non si consuma perché riciclato
Energia libera, G
XY
Ea
XC+Y
EaC
Il catalizzatore diminuisce Ea
facendo percorrere alla reazione un
cammino diverso senza variare il
valore di DG
Il catalizzatore non rende spontaneo
un processo endoergonico
X+Y
DG
X-Y
coordinata di reazione
16
L’azione del catalizzatore (2)
Es1: Esterificazione di un acido carbossilico
O
H3C
O
C
H3C
OH
H
O
H2O
C
CH3
OCH3
La reazione è lenta ma viene accelerata aggiungendo un acido inorganico alla miscela di reazione
+
O
H3 C
C
+
+
H3 C
OH
C
OH
OH H
OH
OH
O
H3C- C - O
CH3
OH
O
CH3
OH
+
H3 C
C
OH
H
H
OH
H3C- C- O-CH3
+
CH3
OH
H+
HOH
OH
C
H3 C
OH
H3C -C
H
OH
H+
H3 C
+
C
OH
O
CH3
H3 C
C
O
O
CH3
17
L’azione del catalizzatore (3)
Es2:
2H202 → 2H2O + O2
G
Ea
H202
Eac
DGr
2H2O+O2
coordinata di reazione
DG°= -50,2 Kcal/mol
1) H2O2+2Fe+2+2H+→2H2O+2Fe+3
2) H2O2 + 2Fe+3 →O2+2H++2Fe+2
2H2O2
Fe+2 , H+
2H2O + O2
Fe+2 e H+ = catalizzatori
Le bollicine di O2 che si
sviluppano quando si
versa H2O2 su una ferita
sanguinante sono dovute
all’azione catalitica della
catalasi, un enzima
presente nel sangue
18
Catalisi omogenea
Il catalizzatore e i reagenti sono nella stessa fase
Es: 1)H2O2 + I- →H2O + IO2)H2O2 + IO- →H2O + O2+ I2H2O2
→ 2H2O +O2
19
Catalisi eterogenea
Il catalizzatore e i reagenti NON sono nella stessa fase
Es1: 2H202
MnO2
→
2H2O + O2
Es2:
CxHy + a O2  b CO2 + c H2O
2 CO + O2  2 CO2
2 NO  O2 + N2
2 NO2  2 O2 + N2
Marmitta Catalitica
Al2O3
20
Equilibrio chimico e velocità di reazione (1)
t=0
R
k1
k-1
k1
t=eq
R
P
r
v  k1[ R ]
P
k-1
k1[ R]eq  k1[ P]eq
r s
vv
s
v  k 1[ P]
r s
vv
k 1 [ P]eq

 Keq
k1 [ R]eq
21
Equilibrio chimico e velocità di reazione (2)
In generale per una reazione reversibile:
aA + bB +   pP + qQ + 
k1 [P]p • [Q]q • • •
Keq =
=
k -1 [ A ]a • [B]b • • •
All’equilibrio avremo:
Se l’equazione è scritta nella forma inversa:
pP + qQ +   aA + bB + 
a
b
k -1 [ A ] • [B] • • •
K' eq = = p
q
k1 [P] • [Q] • • •
1
da cui: K' eq =
Keq
22
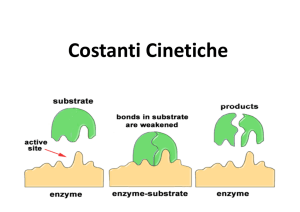
Cinetica Enzimatica
“In vivo” ogni reazione è catalizzata da un enzima specifico
Enzimi:
Proteina (PM12.000÷1.000.000)
Alto potere catalitico in condizioni blande
di T, P e pH
Elevata specificità e assenza di sottoprodotti
Possibilità di regolazione fine
Composizione
CATENA POLIPEPTIDICA ÷ COFATTORE
Apoenzima
Coenzima o Gruppo prostetico
Oloenzima
(se legato covalentemente)
23
Gli enzimi sono classificati in base alle reazioni che
catalizzano
24
Azione catalitica dell’enzima (1)
L’aumento della velocità di reazione può
variare di parecchi ordini di grandezza
Es: Anidrasi carbonica
107
Fosfofruttomutasi
1012
Ureasi
1014
25
Azione catalitica dell’enzima (2)
Effetto prossimità:
l’enzima facilita l’urto efficace
mediante un “aiuto sterico”
26
Azione catalitica dell’enzima (3)
Un esempio di “Effetto di prossimità” nelle
razioni organiche
27
Azione catalitica dell’enzima (4)
Stereospecificità del sito catalitico
28
Azione catalitica dell’enzima (5)
Stiramento e/o distorsione del legame da rompere
29
Analisi equazione di Michaelis & Menten
E+S
Km 
k
k1
k-1
kcat
ES  P + E

Kcat
k +k
K =
k
K1
1
-1
m
Vmax • [S]
vo =
K m + [S]
cat
1
Vmax
Vmax • [S]
=
2
K m + [S]
2[S] = K m + [S]
[S] = K m
30
Grafico dei doppi reciproci (Lineweaver & Burk)
Vmax • [S]
Vo =
K m + [S]
1 K m + [S]
Km
[S]
=
=
+
v o Vmax • [S] Vmax • [S] Vmax • [S]
1
Km
1
1
=
•
+
Vo
Vmax [S] Vmax
31
Significato di Km (1)
Es1: confronto dei valori di Km
tra due enzimi con
i relativi substrati
Il valore di Km indica il
grado di affinità di un enzima
per un certo substrato
Anidrasi carbonica
Fosfofruttomutasi
Ureasi
107
1012
1014
32
Significato di Km (2)
Es2: Confronto dei valori di Km
della Esochinasi con due
substrati diversi
D-Glucosio (S1)
D-Fruttosio (S2)
La Km più alta riflette
una minore affinità
dell’enzima per S 2
La Km più bassa riflette
una maggiore affinità
dell’enzima per S 1
Km=0,05
Km=1,5
Minore è il valore di Km,
maggiore è l’affinità dell’enzima
per quel substrato
33
Significato di Km (3)
Spiegazione alternativa
E+S
k1
k-1
ES
kcat
P+E
k - 1 + kcat se k <<k (ipotesi quasi sempre verificata) avremo:
cat
-1
Km =
k1
k-1
Km =
= Ks
k1
“Costante di Dissociazione” del Complesso ES
ES
k-1
k1
E+S
k - 1 [E][S]
Ks =
=
k1
[ES]
[ES] Alta → Ks bassa → Alta Affinità
34
Significato di Vmax
V0 = kcat [ES]
[ET] = [E] + [ES]
V0
Vmax = kcat [ET]
Vmax3
Vmax è una misura della
concentrazione enzimatica
e si esprime in
Vmax2
Vmax1
[E3]>[E2]>[E1]
[S]
Unità Internazionali (U)
1U= Quantità di enzima che catalizza
la formazione di 1mM di prodotto
per min in condizioni definite (pH, T, ...)
Conoscendo [ET] e Vmax si può calcolare Kcat
Vmax
Kcat =
[E T ]
“Costante catalitica” o “Numero di turnover”
(mM di substrato trasformate per min)
35
Effetto del pH sulla stabilità e attività dell’enzima
S
P


E
S
ES

E
H+
E
S

E

ES


OH- 

ES


36
Effetto della Temperatura
sulla stabilità e attività dell’enzima
Risultato di due processi concorrenti:
Aumento di V0 all’aumentare di T
k = A·e-Ea/RT
(vedi teoria degli urti di Arrenius)
T ottimale
Diminuzione di V0 a temperature
superiori a quella ottimale per la
rottura di legami deboli della
struttura terziaria della catena
polipeptidica della proteina
(vedi denaturazione delle proteine)
37
Inibizione enzimatica
L’inibizione (Reversibile o Irreversibile) è uno dei maggiori
sistemi di regolazione del metabolismo
Inibizione Irreversibile
E+S
k1
k-1
kcat
ES  P + E
Km =
Vmax 
+
I  EI “Complesso abortivo irreversibile”
Es: Inibizione dell’ Acetilcolinesterasi con il gas nervino
Diisopropilfluorofosfato (DIFP) (“Inibitore suicida” vedi anche 5F-U)
O CH3
O CH3
E
..
CH -OH + F-P-O-CH
2
Acetilcolinesterasi
(degrada l’acetilcolina)
O
CH3
H3C-CH-CH3

E
CH2-O -P-O-CH + HF
O
CH3
H3C-CH-CH3
38
Vm ax [S]
vo =
[I]
(
K m 1+ Ki ) + [S]
•
Inibizione Competitiva (IC)
Km app
1
Km
1
[I ] 1
=
1+
•
+
Ki [S] Vm ax
v o Vm ax
( )
Vmax =
Kmapp 
39
Inibizione Competitiva (2)
Es1: Antimetaboliti (sulfamidici, pro-farmaci analoghi di
basi e
nucleosidi purinici e pirimidinici)
NH2
COOH
NH2
O=S=O
H–N–R
Parte essenziale per l’attività
Acido
Timidilato Sintetasi
dUMP
dTMP
p-aminobenzoico
Diidrofolato Sintetasi
(Solo batterica)
Acido Folico
R=H: Sulfanilamide
“Antagonizza”
l’incorporazione dell’acido
p-aminobenzoico
nell’acido folico
DNA
Negli animali non esiste
la diidrofolato reduttasi.
L’acido folico deve essere
assunto dalla dieta
(vitamina)
40
Inibizione Competitiva (3)
Es2: Analogo non metabolizzabile
COOCH2
CH2
COO-
Succinato
COOCH2
COO-
Fumarato
E-FAD
E-FADH2
COOCH
HC
COO-
)+
Succinico deidrogenasi
Sito attivo
)+
Malonato
41
Inibizione Competitiva (4)
Es3: Analogo metabolizzabile
H H
H C-C-O-H
H H
Etanolo
H
H C-O-H
H
Metanolo
H
H C-C=O
H H
NAD
NADH + H+
Alcool deidrogenasi
Acetaldeide
H
H
C=O
Formaldeide
Idrossimetila
proteine
e acidi nucleici
30 ml di metanolo
sono letali
42
Inibizione Non Competitiva (INC)
Vm ax
Vo =
Vmax 
Km =
1 Km
=
v o Vm ax
1+
[I]
Ki
• [S]
K m + [S]
1
1
• +
[S] Vm ax
( )
[I]
1+
Ki
( )
1+
[I]
Ki
43
Inibizione Incompetitiva (IIC)
Vm ax
1+
Vo =
Vmax

Kmapp 
[I]
Ki
Km
1+
• [S]
[I]
+ [S]
Ki
1
Km
1
1
[I ]
=
•
+
1+
ki
v o Vm ax [S] Vm ax
(
)
44
Schema riassuntivo dei grafici dei doppi reciproci
IC, INC, IIC
Vmax 
Kmapp 

1
Km
1
[ I] 


  1 

v o Vma x Vma x 
Ki 
45
Enzimi oligomerici
Km K0.5
Macromolecole proteiche
a più subunità
(monomeri o protomeri)
Se i siti catalitici sono
indipendenti (non
cooperativi) avremo
enzimi con “cinetica
classica Micheliana”
(V0/[S] curva iperbolica)
Se i siti sono dipendenti
(cooperativi) avremo
“enzimi allosterici”
(V0/[S] curva sigmoide)
46
Enzimi allosterici
L’interazione (binding)
di una molecola di
“legando” (substrato,
inibitore, attivatore) con
un sito catalitico di una
subunità, modifica il
binding, aumentando
o diminuendo l’affinità
degli altri siti liberi
Interazioni omotropiche:stesso legando (substrato)
Interazioni eterotropiche:legandi diversi (substrato,inibitore,attivatore)
47
Regolazione degli enzimi allosterici (1)
Interazioni Omotropiche
C
-
S
C
S
C
+
V0
S
½ Vmax
C
S
K0.5
S
C
C
[S]
S
48
Regolazione degli enzimi allosterici (2)
Interazioni Eterotropiche
► Substrato
● Modulatore positivo(Attivatore)
■ Modulatore negativo (Inibitore)
C
S
S
S
R
+
C
R

49
Due possibili modulazioni allosteriche
Vmax 
K0.5 =
Vmax =
K0.5 
50
Enzimi allosterici: chiave di controllo nella regolazione metabolica
Gli enzimi allosterici si trovano spesso
in punti strategici delle vie metaboliche
ed agiscono con “effetto switch on-off”
51