La distribuzione normale

Tempi di reazione
Strumenti di indagine
per la valutazione psicologica
●
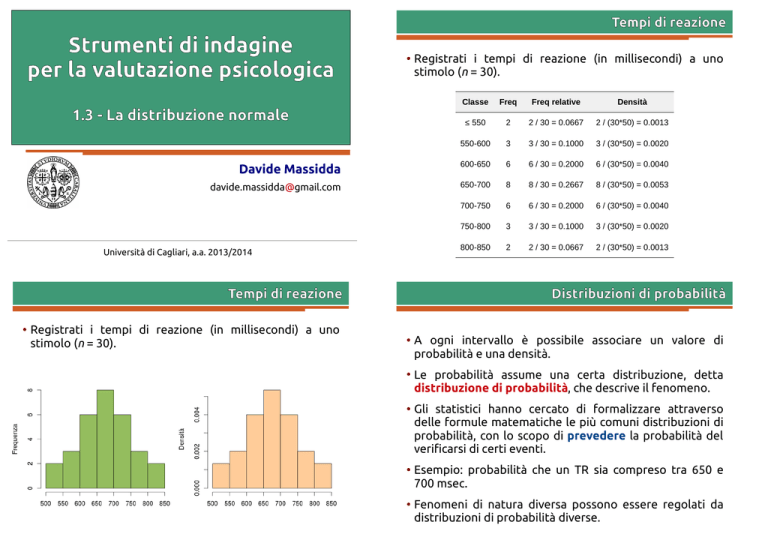
Classe
Freq
Freq relative
Densità
≤ 550
2
2 / 30 = 0.0667
2 / (30*50) = 0.0013
550-600
3
3 / 30 = 0.1000
3 / (30*50) = 0.0020
Davide Massidda
600-650
6
6 / 30 = 0.2000
6 / (30*50) = 0.0040
[email protected]
650-700
8
8 / 30 = 0.2667
8 / (30*50) = 0.0053
700-750
6
6 / 30 = 0.2000
6 / (30*50) = 0.0040
750-800
3
3 / 30 = 0.1000
3 / (30*50) = 0.0020
800-850
2
2 / 30 = 0.0667
2 / (30*50) = 0.0013
1.3 - La distribuzione normale
Università di Cagliari, a.a. 2013/2014
Tempi di reazione
●
Registrati i tempi di reazione (in millisecondi) a uno
stimolo (n = 30).
Registrati i tempi di reazione (in millisecondi) a uno
stimolo (n = 30).
Distribuzioni di probabilità
●
●
●
●
●
A ogni intervallo è possibile associare un valore di
probabilità e una densità.
Le probabilità assume una certa distribuzione, detta
distribuzione di probabilità, che descrive il fenomeno.
Gli statistici hanno cercato di formalizzare attraverso
delle formule matematiche le più comuni distribuzioni di
probabilità, con lo scopo di prevedere la probabilità del
verificarsi di certi eventi.
Esempio: probabilità che un TR sia compreso tra 650 e
700 msec.
Fenomeni di natura diversa possono essere regolati da
distribuzioni di probabilità diverse.
Le funzioni che descrivono la probabilità
●
Queste formule matematiche sono dette:
La distribuzione normale
●
Funzioni di probabilità (variabili discrete)
Funzioni di densità di probabilità (variabili continue)
●
●
●
Le prime associano, a ogni valore che la variabile può
assumere, una certa probabilità di occorrenza.
●
Le seconde associano, a ogni intervallo di valori che la
variabile può assumere, una certa probabilità di
occorrenza.
●
●
La distribuzione normale
µ
Fa riferimento a variabili casuali continue ed è definita
per valori compresi tra tra -∞ e +∞.
La probabilità di un fenomeno che si distribuisce “come
una normale” è massima nell'intorno di un determinato
valore, chiamato μ.
Più un intervallo si allontana dal valore μ, minore sarà la
probabilità che un valore ricada all'interno di tale
intervallo.
Allontanandosi dal valore μ, la probabilità decresce in
maniera simmetrica per valori maggiori e minori di μ.
In una variabile che si distribuisce normalmente, moda,
mediana e media coincidono tutte col parametro μ.
La distribuzione normale
µ
La distribuzione normale
Funzione di ripartizione
In una distribuzione normale, l'area compresa tra i due
estremi di un intervallo è definita dalla seguente funzione
di probabilità cumulata (funzione di ripartizione normale):
Attraverso la funzione di ripartizione possiamo calcolare la
probabilità che un dato ricada tra -∞ e un certo punto z.
b
z
1
e
−∞ σ √ 2 π
2
1 x−μ
σ )
− (
1
p(a≤ x≤b)=∫
e 2
a σ √2 π
p= ∫
dx
p
●
x è il valore noto che il fenomeno può assumere;
●
π è la costante “pi greco” (approssimato: 3.14)
●
e è il numero di Nepero (approssimato: 2.72)
●
µ e σ sono i parametri della distribuzione.
1-p
N.B. #1 L'area sottesa dalla
curva rappresenta una
probabilità.
0
z
+∞ →
Il parametro σ
σ=1
●
●
È il valore nell'intorno del quale si registra il picco
massimo di probabilità.
Distribuzioni con diverso μ hanno il loro picco massimo di
probabilità in punti diversi del continuum.
dx
N.B. #2 Complessivamente,
l'area sottesa dalla curva
vale 1 (perché la probabilità
varia tra 0 e 1).
← -∞
Il parametro μ
2
1 x−μ
− ( σ )
2
Il parametro σ
Il parametro σ
σ=1
σ=1
σ = 1.5
σ = 1.5
σ=3
Il parametro σ
●
●
●
All’aumentare di σ la campana si schiaccia e si allarga: la
probabilità si concentra sempre meno su μ e aumenta per
valori via via sempre più distanti da μ.
Quindi, all'aumentare di σ, si riduce sempre più la
probabilità che si presenti un valore nell'intorno di μ e
aumenta la probabilità che si presentino altri valori da
esso distanti.
All'aumentare di σ aumenta la variabilità del fenomeno.
Il parametro σ
●
Se per valori piccoli di σ il fenomeno è moto prevedibile
(quasi certamente assumerà un valore nei pressi di μ)...
...per valori grandi di σ, anche valori compresi in intervalli
distanti da μ avranno buona probabilità di presentarsi:
aumenta l'incertezza.
Gli stimatori
●
Data una variabile casuale x che segue una distribuzione
normale, i parametri μ e σ possono essere stimati
rispettivamente attraverso la media e la deviazione
standard della variabile.
n
∑ xi
μ=
̂
●
i=1
n
̂
σ=
√
La distribuzione normale standardizzata
●
●
n
∑ ( x i− ̄x )2
i=1
n−1
I valori dei parametri μ e σ sono conoscibili solo avendo a
disposizione tutti valori della popolazione di riferimento.
Tuttavia, utilizzando un campione rappresentativo della
popolazione, essi possono essere stimati.
●
●
Esistono infinite distribuzioni normali, ognuna descritta
da un proprio μ e un proprio σ.
Per poter confrontare fra loro variabili sì tutte “normali”,
ma ognuna descritta da un proprio μ e un proprio σ, è
possibile far riferimento a una stessa distribuzione
normale di riferimento.
La distribuzione normale di riferimento ha μ = 0 e σ = 1 ed
è detta “standardizzata”.
Tutte le distribuzioni normali possono essere
standardizzare e portate su una scala comune (es. voti).
Standardizzare una variabile
Un esempio pratico
La variabile x viene trasformata in punti z. La media della
nuova variabile z avrà M = 0 e SD = 1.
Assumendo che la distribuzione dei voti del prof. Nepero
sia normale, qual è la probabilità di osservare un voto
superiore a 28? (Vedi lezione 1.2)
x i−μ
z i= σ
x −̄
x
z i= i
s
̄x =25.17
̄s =2.70
z 28=
28−25.17
=1.05
2.70
p(−∞≤x≤1.05)=0.85
p( x >28)=1−0.85=0.15
Un esempio pratico
Assumendo che la distribuzione dei voti del prof. Nepero
sia normale, qual è la probabilità di osservare un voto
superiore a 28? (Vedi lezione 1.2)
0.85
1 – 0.85 = 0.15
La tavola della normale
●
Le tavole della distribuzione normale standard
forniscono alcuni valori di probabilità, già calcolati
attraverso la funzione di ripartizione, per valori compresi
tra 0 e alcuni punti z.
z
0
1
0.0 .0000 .0040
0.1 .0398 .0438
...
...
...
1.0 .3413 .3438
...
...
...
...
5
...
...
...
...
...
...
... .3531
...
...
1 – (0.5 + 0.3531) = 0.1469
-∞
z = 1.05
Esercizio
●
Data una distribuzione di tempi di reazione con:
̄x =676.84
s=80.25
assumendo una distribuzione normale, calcolare la
probabilità di osservare un TR compreso tra 550 e 750
msec.
...
...
...
...
...
...
Esercizio
Area compresa
tra 0 e z = -1.58
z 550 =
550−676.84
=−1.58
80.25
Area compresa
tra 0 e z = 0.91
z 750 =
750−676.84
=0.91
80.25
Esercizio
P = 0.4429 + 0.3186 = 0.7615
La distribuzione dei tempi di reazione
Nota bene
●
0.4429
0.3186
Nel lavorare con i TR, di solito si assume la normalità
distributiva, ma spesso questa assunzione risulta violata.
●
●
z 550 =−1.58
z 750 =0.91
Sono stati formulati diversi
modelli
cognitivi
per
spiegare l'asimmetria della
distribuzione.
Uno molto celebre prevede
che il TR sia il risultato della
somma di due componenti:
una decisionale e una di
trasduzione.