I numeri interi
Si assume l’esistenza dell’insieme numerico Z dei numeri interi
come ampliamento dei numeri naturali. Tale insieme è dotato
delle due ordinarie “operazioni” di addizione e moltiplicazione
che verificano le seguenti proprietà. Per ogni a, b, c ∈ Z si ha:
1. (a + b) + c = a + (b + c) (associatività della somma);
2. a + b = b + a (commutatività della somma);
3. esiste un’unico elemento di Z, 0, tale che a + 0 = 0 + a (esistenza elemento neutro per la somma);
4. a + (−a) = 0 (esistenza dell’opposto);
5. (a · b) · c = a · (b · c) (associatività della moltiplicazione);
6. a · b = b · a (commutatività della moltiplicazione);
7. esiste un’unico elemento di Z, 1, tale che a·1 = 1·a (esistenza
elemento neutro per moltiplicazione);
8. a · (b + c) = a · b + a · c, (a + b) · c = a · c + b · c (distributività
della moltiplicazione rispetto alla somma).
Da queste ne conseguono altre di seguito elencate.
Proposizione 1 Siano a, b interi. Allora:
(i) a · 0 = 0 = 0 · a;
(ii) (−a) · b = −(a · b);
(iii) (−a) · (−b) = a · b;
(iv) a · b = 0 ⇐⇒
prodotto);
a = 0 ∨ b = 0 (legge di annullamento del
(v) a · c = b · c, c 6= 0 =⇒ a = b (legge di cancellazione).
Teorema 1 (Divisione in Z) Siano a, b ∈ Z, b 6= 0. Allora esistono e sono unici q, r ∈ Z tali che
1. a = qb + r
2. 0 ≤ r < |b|.
Si dice che q è il quoziente ed r il resto della divisione di a per b.
È chiaro che
r = 0 ⇔ b|a.
Proposizione 2 Per ogni a, b, c ∈ Z∗ si ha:
1. a|b ⇒ a|(−b) ∧ −a|b ∧ −a|(−b)
2. a|b ∧ a|c ⇒ a|(b ± c)
3. a|b ⇒ a|(bc)
4. a|b ∧ b|c ⇒ a|c
5. a|b ∧ b|a ⇒ b = ±a
6. Se a, b sono interi positivi e a|b, allora a ≤ b
Definizione 1 Siano a, b ∈ Z, a, b non entrambi nulli. Si dice
massimo comun divisore di a e b un intero d ∈ Z tale che
• d|a
∧
d|b
• Per qualsiasi altro d0 ∈ Z tale d0|a
∧
d0|b si ha d0|d.
Osservazione 1 Si fa esplicitamente osservare che si parla di un
massimo comun divisore e non del massimo comun divisore tra
due interi. Infatti se d è massimo comun divisore, lo è anche −d.
Inoltre, se d è massimo comun divisore tra a e b, lo è anche tra
−a e b, tra a e −b e tra −a e −b. Infine, se uno dei due interi della
definizione è 0, per esempio a = 0, allora b è massimo comun
divisore tra a e b. Infatti b|b, b|0 e se d0 ∈ Z è tale che d0|a e d0|b,
ovviamente d0|b.
Teorema 2 (Esistenza del massimo comun divisore) Siano a, b ∈
Z∗. Allora sicuramente esiste un massimo comun divisore d tra
a e b. Inoltre esistono due numeri interi s e t tali che
d=s·a+t·b
(Identità di Bézout).
Infine, l’unico altro massimo comun divisore è −d.
Quindi esiste un unico massimo comun divisore positivo e si
indica con MCD(a, b). Nel seguito quando si parlerà del massimo
comun divisore tra due interi ci si riferirà sempre a quello positivo.
In tal caso, il MCD è il più grande divisore positivo comune, non
solo rispetto alla relazione d’ordine totale ≤, ma anche rispetto
alla divisibilità. Più precisamente, se Da e Db sono gli insiemi dei
divisori positivi di a e b, rispettivamente, allora
MCD(a, b) = max(Da ∩ Db) = max(Da ∩ Db)
≤
|
Due interi a, b si dicono coprimi se MCD(a, b) = 1.
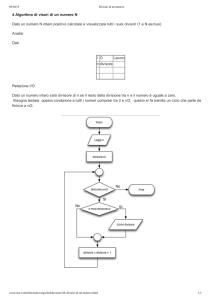
Algoritmo delle divisioni successive
Per determinare il massimo comun divisore tra due fissati interi
a, b con a, b 6= 0 si procede nel seguente modo. Intanto, come
gia osservato, il massimo comun divisore non cambia se si cambia segno ad uno dei due dati interi o ad entrambi. Pertanto
possiamo senz’altro supporre a, b positivi. Si effettua la divisione
euclidea tra a e b, ottenendo cosı̀ un resto r1. Se r1 = 0 la procedura si arresta e MCD(a, b) = b. Altrimenti, si continua operando
la divisione tra b ed r1, ottenendo un resto r2. Se r2 = 0, allora
il procedimento si ferma e MCD(a, b) = MCD(b, r1) = r1. Altrimenti, si prosegue effettuando la divisione tra r1 e r2, e cosı̀ via,
iterando il procedimento. Dopo un numero finito di passi, diciamo n, si perviene sicuramente ad una divisione con resto nullo.
Allora il massimo comun divisore tra a e b coincide esattamente
con l’ultimo resto non nullo, ossia quello della (n − 1)-esima divisione.
In sintesi, si eseguono le seguenti divisioni fino a quando il resto
è zero:
a = q1b + r1 0 ≤ r1 < |b|
b = q2r1 + r2 0 ≤ r2 < r1
r1 = q3r2 + r3 0 ≤ r3 < r2
...
rn−3 = qn−1rn−2 + rn−1 0 ≤ rn−1 < rn−2
rn−2 = qnrn−1 rn = 0.
Allora
MCD(a, b) = rn−1.
Ciò consente anche di trovare una coppia di interi (s, t) prevista
dal teorema precedente: procedendo a ritroso da rn−1 = rn−3 −
qn−1rn−2 ed utilizzando le relazioni trovate ad ogni divisione, si
ricava l’identità di Bézout.
Esempio. a = 212 e b = 148. b non divide a. Effettuando la
divisione si ha:
212 = 148 + 64,
con r1 = 64 6= 0. Si continua quindi con la divisione tra b ed r1,
ottenendo
148 = 2 · 64 + 20,
con r2 = 20 6= 0. Si prosegue ancora dividendo r1 per r2:
64 = 3 · 20 + 4,
con r3 = 4 6= 0. Infine la divisione tra r2 ed r3 dà resto nullo
r4 = 0. Pertanto
MCD(212, 148) = r3 = 4.
Per avere l’identità di Bézout, si ricava 4 dall’ultima relazione
scritta, cioè 4 = 64 − 3 · 20. Poi 20 dalla divisione di cui è resto
e lo si sostituisce:
4 = 64 − 3 · 20 = 64 − 3 · (148 − 2 · 64) = 7 · 64 − 3 · 148.
In conclusione, ricavando 64 dalla prima divisione, si ha:
4 = 7 · 212 + (−10) · 148.
Definizione 2 Siano a, b ∈ Z∗. Si dice minimo comune multiplo tra a e b un intero m ∈ Z tale che
• a|m ∧ b|m
• ∀m0 ∈ Z tale che a|m0 ∧ b|m0 si ha m|m0.
Anche in questo caso si parla di un minimo comune multiplo
e non del minimo comune mutiplo. Tuttavia, si dimostra che
se m0 è un’altro minimo comune multiplo tra due interi a e b,
allora m0 = −m. Quindi esiste un’unico minimo comune multiplo
positivo e lo si indica con mcm(a, b).
Teorema 3 Siano a, b ∈ Z∗. Se d è un massimo comun divisore
di a e b, allora ab
d è un minimo comune multiplo tra a e b. In
particolare, vale la formula
mcm(a, b) =
|ab|
.
MCD(a, b)
Equazioni Diofantee
L’identità di Bézout permette di risolvere equazioni lineari del
tipo descritto nella seguente definizione
Definizione 3 Si dice equazione Diofantea un’equazione in Z
nelle incognite x, y della forma
ax + by = c
(1)
dove a, b ∈ Z, non entrambi nulli e c ∈ Z.
Teorema 4 Siano a, b, c ∈ Z, a, b non entrambi nulli e sia d =
MCD(a, b). Allora si ha:
1. l’equazione Diofantea (1) ha soluzioni se e soltanto se d | c
(dimostrata a lezione);
2. se (1) ha soluzioni, detta (x0, y0) una di esse, tutte le altre
sono di tipo (x0 + b̄h, y0 − āh), h ∈ Z, dove ā = ad , b̄ = db
(parzialmente dimostrata a lezione).
Definizione 4 Sia p ∈ Z, p 6= −1, 0, 1. Si dice che p è primo se
gode della seguente proprietà:
(p|a · b, a, b ∈ Z) =⇒ (p|a ∨ p|b).
Osservazione 2 L’essere un intero primo si può esprimere equivalentemente come:
(p = a · b, a, b ∈ Z) =⇒ (a, b ∈ {±1, ±p}).
Per questo motivo i numeri primi sono anche detti irriducibili.
Segue che un numero intero p diverso da 0 e da ±1 è primo se
e solo se gli unici suoi divisori sono quelli banali, cioè ±1, ±p.
Naturalmente se p è un intero primo, lo è anche −p.
Teorema 5 (Teorema fondamentale dell’Aritmetica) Tutti i
numeri interi diversi da zero e da ±1 si fattorizzano in modo essenzialmente unico nel prodotto di un numero finito di primi. Più
precisamente, per ogni z intero 6= 0, ±1 o z è primo o si ha:
h
s
z = ±p11 · · · ph
s ,
pi > 1 primi distinti
METODI DI FATTORIZZAZIONE
1. CRIVELLO DI ERATOSTENE
Per determinare i numeri primi minori o uguali di un assegnato
numero naturale m ≥ 4, si scrive una tabella con tutti i numeri
fino ad m e si comincia con il cancellare i multipli di 2. Finita
questa operazione, si eliminano tutti i multipli del primo numero
non cancellato, ovvero 3; dopo i multipli di 5, che è il primo
numero non cancellato, dopo 7, e cosı̀ via fino al più grande
√
numero primo q più piccolo di m. Infatti se p è un numero
√
primo più grande di
m un suo multiplo tramite un numero
√
primo più piccolo di m eventualmente presente nella tabella è
stato già scartato e già p2 > n.
Osservazione 3 Tra i fattori primi di un numero naturale (ci
si può sempre riferire a questo caso senza ledere la generalità)
n ≥ 4 c’è n’è almeno uno minore o uguale a
√
n. Sia infatti
h
s
n = p11 · · · ph
s
la scomposizione di n in fattori primi. Se fosse
√
√
p1 > n, . . . , ps > n,
allora sarebbe
h
s
n = p11 · . . . · ph
s >n
il che è una contraddizione.
Esempio Se si vuole fattorizzare il numero n = 4187, si considera
√
la sua radice n v 64, 707 e quindi si prendono in esame tutti i
numeri primi minori di 64. Essi sono:
2, 3, 5, 7, 11, 13, 17, 19, 23, 31, 37, 41, 43, 47, 53, 59, 61.
Effettuando (se necessario) le divisioni con la calcolatrice si ottiene un eventuale primo fattore. Se non si trova nessun fattore,
il numero è irriducibile. In queso caso si vede che n è divisibile
per 53 e precisamente n = 53 · 79.