Esercizi Amplificatori Operazionali - Pacinotti

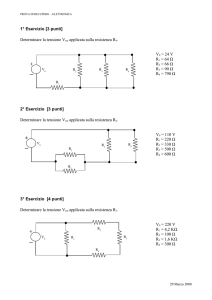
Esercizi su Amplificatori Operazionali
Esercizio 1.
vR4
vR1
iR4
R1
iR1
R2
R4
vd
v1
v2
v+
R3
vout
Con riferimento al circuito in figura, esprimere la tensione vout in funzione delle tensioni v1 e v2.
Soluzione
vout
dell’operazionale, fintanto che questo opera in linearità, è
vd
molto elevata (idealmente infinita). Dal momento che il valore della tensione vout è limitato dalla
v
dinamica di uscita del circuito, la tensione differenziale di ingresso vd = out è pressoché nulla
Ad
L’amplificazione differenziale Ad =
( vd = v + − v − ≅ 0 ) e, di conseguenza, essendo l’impedenza di ingresso dell’operazionale (Zin) non
nulla, le correnti entranti negli ingressi dell’operazionale sono a loro volta pressoché nulle
v
( i + = −i − = d ≅ 0 , vedi dispense di teoria).
Z in
Sulla base di queste considerazioni, si può risolvere l’esercizio assumendo (amplificatore
operazionale ideale):
vd = v + − v − = 0
(1)
i + = −i − = 0
(2)
Applicando la legge di Kirchoff delle tensioni è possibile scrivere la tensione di uscita del circuito
in figura come:
vout = −vR4 − vd + v + = −vR4 + v +
(3)
dove, nell’ultimo passaggio, si è considerata la (1).
Le tensioni v + e vR4 nella (3), essendo il circuito lineare, possono essere ricavate applicando il
principio di sovrapposizione degli effetti, tenendo conto delle (1-2), come illustrato qui di seguito.
Calcolo di v +
Dalla (2) si osserva che la corrente al morsetto “+” dell’operazionale è sempre nulla, per cui la
presenza dell’amplificatore operazionale non ha alcun influsso sul circuito collegato al morsetto “+”
e la tensione v + può essere calcolata immaginando il circuito v2-R2-R3 scollegato
dall’operazionale.
Sfruttando questa considerazione, applicando il principio di sovrapposizione degli effetti (le
grandezze con un apice si riferiscono al contributo di v1, le grandezze con due apici, al contributo di
v2 )
R3
v + = v + '+ v + ' ' = 0 +
v2
(4)
R 2 + R3
Si osserva che i generatori non collegati al morsetto “+” (come v1 in figura) non danno contributo a
v + e che il contributo di v2 è stato calcolato utilizzando la regola del partitore di tensione (essendo
i+=0, R2 ed R3 risultano collegate in serie).
Calcolo di vR4
Si osserva che vR4 = R 4 iR 4 e si determina iR 4 utilizzando il principio di sovrapposizione degli
effetti. A tale fine, è possibile considerare il contributo di tutti i generatori collegati al morsetto “+”
includendo un unico generatore di tensione equivalente, di valore dato dalla (4), collegato
direttamente al morsetto “+”
v
v + v1 v2
R3
i R 4 = i R 4 '+i R 4 ' ' = 1 −
=
−
(5)
R1 R1 R1 R1 R 2 + R3
Ne segue che
vR4 =
R4
R 4 R3
v1 −
v2
R1
R1 R 2 + R3
(6)
La tensione di uscita richiesta, risulta quindi espressa dalla (3) come:
vout = −
R4
R 4 R3
R3
R4
R3  R 4 
v1 +
v2 +
v2 = −
v1 +
+ 1v2

R1
R1 R 2 + R3
R 2 + R3
R1
R 2 + R3  R1 
(7)
Esercizio 2.
R4
R1
R2
v1
I0
vout
R3
Con riferimento al circuito in figura, esprimere la tensione vout in funzione di v1 ed I0.
Esercizio 3.
R4
R1
R2
v1
v2
I0
R3
vout
Con riferimento al circuito in figura, esprimere la tensione vout in funzione delle tensioni v1 e v2
e della corrente I0.
Esercizio 4.
R4
R5
R1
R2
v1
v2
vout
I0
Con riferimento al circuito in figura, esprimere la tensione vout in funzione delle tensioni v1 e v2
e della corrente I0.
Esercizio 5.
R5
R2
R1
R3
v1
v2
R4
vout
Con riferimento al circuito in figura, esprimere la tensione vout in funzione delle tensioni v1 e v2.
Esercizio 6.
R2
R5
R3
R1
R4
v1
v2
vout
Con riferimento al circuito in figura, esprimere la tensione vout in funzione delle tensioni v1 e v2.