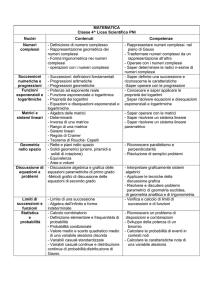
TABELLA RIASSUNTIVA DELLLE COMPETENZE DEL SECONDO BIENNIO
L'ASSE MATEMATICO
Competenze
Abilità
M5a ● Progettare un
percorso risolutivo
strutturato in tappe
M5
Individuare
le strategie
del pensiero
razionale
negli aspetti
dialettici ed
algoritmici
per la
soluzione di
problemi
M5b ● Formalizzare il
percorso di soluzione di
un problema attraverso
modelli algebrici e
grafici
M5c ● Convalidare i
risultati conseguiti sia
empiricamente, sia
mediante
argomentazioni
M5d ● Tradurre dal
linguaggio naturale al
linguaggio algebrico e
viceversa
Conoscenze
● le fasi
risolutive di un
problema e
loro
rappresentazio
ni con
diagrammi
● Principali
rappresentazio
ni di un
oggetto
matematico
● Tecniche
risolutive di un
problema che
utilizzano
formule
geometriche,
equazioni e
disequazioni.
Indicatori di prestazione
per la valutazione degli
esiti
Saper individuare dati e
variabili in un problema.
Scandire un problema in
sottoproblemi.
Saper individuare un
percorso risolutivo.
Saper ipotizzare un
percorso risolutivo e
valutarne l’esattezza o
l’adeguatezza. Individuare
le relazioni tra i dati e le
incognite.
Saper formalizzare
relazioni fra grandezze e
rappresentarle in forma
adeguata.
Saper formalizzare la
risoluzione del problema
attraverso la scrittura di
uguaglianze e/o
disuguaglianze
Saper eseguire un
controllo sul significato
dei valori determinati
come insieme delle
soluzioni del problema.
Saper formalizzare
situazioni problematiche
utilizzando strumenti
algebrici. Utilizzare
equazioni e disequazioni
di primo e secondo grado
per
costruire modelli di
problemi.
Disciplina/Attività
che concorre alla
formazione della
competenza
Matematica
Matematica
Matematica
Matematica
L'ASSE MATEMATICO
Competenze
Abilità
Conoscenze
● Il metodo
delle
M5e ● Riconoscere i
coordinate: il
principali enti, figure e
piano
luoghi geometrici e
cartesiano.
descriverli con
●
linguaggio naturale
Interpretazione
geometrica dei
sistemi di
equazioni.
●Rappresentaz
ione nel piano
cartesiano delle
M5f ● Individuare la
coniche:
proprietà essenziali delle
circonferenza,
M5
figure e riconoscerle in
parabola, ed
Individuare situazioni concrete
iperbole.
le strategie
del pensiero
razionale
negli aspetti
dialettici ed
algoritmici
per la
soluzione di M5g ● Applicare le
principali formule
problemi
relative alla retta e alle
coniche sul piano
cartesiano
M5h ● Teoremi del seno
e del coseno. Formule di
addizione e duplicazione
degli archi.
Indicatori di prestazione
per la valutazione degli
esiti
Disciplina/Attività
che concorre alla
formazione della
competenza
Saper distinguere gli enti
fondamentali della
geometria e utilizzare la
terminologia ed il
simbolismo relativi.
Matematica
Saper riconoscere e
classificare una figura
geometrica associando ad
essa un insieme di
proprietà.
Saper confrontare ed
analizzare figure
geometriche, individuando
invarianti e relazioni e
riconoscere trasformazioni
isometriche.
Matematica
Saper utilizzare
propriamente la
terminologia relativa ai
concetti di congruenza,
equivalenza, similitudine.
Saper rappresentare sul
piano cartesiano punti e
figure geometriche.
Saper associare a una
funzione l il suo grafico
sul piano cartesiano.
Matematica
Saper interpretare il
grafico di una funzione.
Interpretare graficamente
un sistema di primo o di
secondo grado.
Saper applicare la
trigonometria alla
risoluzione di problemi
riguardanti i triangoli.
Matematica
M6
Utilizzare il
linguaggio e
i metodi
propri della
matematica
per
organizzare
e valutare
adeguatamen
te
informazioni
qualitative e
quantitative.
L'ASSE MATEMATICO
● Significato
Saper raccogliere,
di analisi e
organizzare e rappresentare
M6a ●Calcolare limiti e
organizzazione un insieme di dati.
derivate di funzioni
di dati
Saper costruire tabelle di
numerici
dati.
● Il piano
Saper riconoscere una
cartesiano e il relazione tra variabili e
concetto di
M6b● Riconoscere una
ricostruire i parametri
funzione
relazione tra variabili e
caratteristici della legge
●Continuità e che la rappresenta.
formalizzarla attraverso
una funzione matematica limite di una
Saper riconoscere schemi
funzione
analizzare funzioni
di proporzionalità diretta o
● Concetto di inversa e formalizzarli
continue e discontinue.
derivata e
attraverso formule
derivazione di matematiche.
una funzione
M6c ● Analizzare
Saper rappresentare una
●
Massimi,
funzioni continue e
funzione nel piano
discontinue Rappresentare minimi e flessi cartesiano costruendone il
di una funzione grafico.
sul piano cartesiano il
● Studio di una
grafico di una funzione
funzione
M6d ● Analizzare
Utilizzare le funzioni
particolari funzioni :
esponenziali e logaritmiche
esponenziali e
per costruire modelli
logaritmiche.
ecnomici,
Rappresentare sul piano
cartesiano il grafico
Matematica
Matematica
Matematica
Matematica
L'ASSE MATEMATICO
Competenze
Abilità
Conoscenze
● Ipotesi e tesi.
Il principio di
M7a ● Utilizzare le
induzione.
tecniche e le procedure
● Concetti di
del calcolo aritmetico ed algoritmo
algebrico
ricorsivo e di
algoritmo
iterativo.
M7b ● Significato della
● Concetto di
probabilità e sue
probabilità di
valutazioni. Probabilità
un evento e
M7
composta, eventi
Utilizzare i
variabili
indipendenti. Elementi di
concetti e i
casuali.
statistica descrittiva.
modelli delle
● Elementi di
scienze
statistica
sperimentali
descrittiva
per studiare M7c ● Tradurre istruzioni ● Equazioni
fenomeni
in sequenze simboliche ; esponenziali e
sociali e
logaritmiche
risolvere sequenze di
naturali e per operazioni e problemi
● Equazioni e
interpretare i sostituendo alle variabili
disequazioni
dati.
letterali i valori numerici. algebriche di
grado superiore
al secondo.
● sistemi di
equazioni e
disequazioni di
M7d ● Risolvere
equazioni e verificare la grado superiore
al secondo
correttezza dei
● Progressioni
procedimenti utilizzati.
aritmetiche e
geometriche
Indicatori di prestazione
per la valutazione degli
esiti
Ricavare ed applicare le
formule per i termini di
una progressione
aritmetica o geometrica.
Disciplina/Attività
che concorre alla
formazione della
competenza
Matematica
Calcolare la probabilità di
eventi elementari.
Calcolare i valori medi ed
Matematica
alcune misure di
variabilità di una
distribuzione statistica.
Saper utilizzare le
variabili nella
generalizzazione di
problemi e determinare i
risultati in formule
algebriche. Associare ad
Matematica
una espressione un
significato funzionale
mediante
l’assegnazione di valori
alle sue variabili.
Saper utilizzare metodi
grafici e numerici per
risolvere equazioni e
disequazioni esponenziali
e logaritmiche.
Matematica