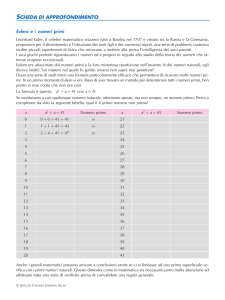
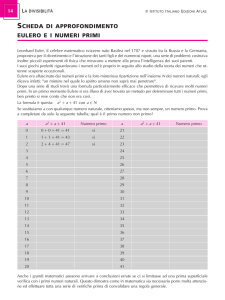
Esercizi sui numeri complessi per il dodicesimo
foglio di esercizi
6 dicembre 2010
1
Numeri complessi radici ed equazioni
Ricordiamo innanzitutto che dato un numero complesso z = x + iy, il suo
coniugato, indicato con z è il numero complesso z = x−iy. Risulta allora che
|z|2 = zz, e che z −1 = z/|z|2 . Ricordiamo anche che, se z = x + iy, il numero
reale x si chiama la parte reale di z, in simboli, <z = x, mentre il numero
reale y si chiama parte immaginaria di z, in simboli =z = y. Ricordiamo
infine che ogni numero complesso può essere espresso nella forma
z = ρ(cos θ + i sin θ),
dove ρ = |z| è la distanza di z dall’origine e θ (determinato a meno della
aggiunta di un multiplo intero di 2π) è l’angolo (espresso in radianti) che il
vettore di componenti <z e =z forma con l’asse delle x.
Esercizio 1 Calcolare il modulo dei seguenti numeri complessi:
1 − 2i,
1 − 2i
,
i−2
i
,
2i − 3
i(1 + i)2 ,
i
i−2
+
,
i+1 i−1
i
(i + 1)(2i − 1)
Nell’ambito dello studio delle funzioni di variabile reale abbiamo definito,
per ogni intero positivo
n, la funzione, definita per valori non negativi di x,
√
1/n
n
f (x) = x
= x, come il numero non negativo f (x) tale che (f (x))n =
x. Questa funzione risulta definita per tutti i valori non negativi di x ed
assume solo valori non negativi. Queste restrizioni sono state adottate perché
eravamo interessati a definire e studiare una funzione e non a trovare tutti i
numeri t tali che tn = x (anche perché sapevamo che il problema di trovare
tutti i numeri t tali che tn = x non avrebbe avuto una soluzione completa
nei numeri reali, in quanto, ad esempio l’equazione t2 = −1 non ha soluzioni
reali.)
1
Una volta introdotti i numeri complessi vale invece la pena di porci il
problema di trovare tutti i numeri (complessi) z che soddisfano all’equazione:
z n = w,
(1)
dove n è ancora una volta un intero positivo e w è un numero complesso
assegnato.
Per risolvere questo problema dobbiamo ricordare la formula che ci fornisce la forma trigonometrica di z n a partire dalla forma trigonometrica di
z. Ricordiamo cioè che se
z = ρ(cosθ + i sin θ),
allora
z n = ρn (cos nθ + i sin nθ).
(2)
Questa formula è una conseguenza delle formule di addizione di sin θ e
cos θ, che ci permettono di dire che
(cos(α + β) + i sin(α + β)) = (cos α + i sin α)(cos β + i sin β).
Una volta introdotta la notazione (cosiddetta formula di Eulero)
eiθ = cos θ + i sin θ,
la stessa formula può essere vista come una conseguenza della proprietà dell’esponenziale di trasformare le somme in prodotti, e cioè come una conseguenza
della formula
ei(α+β) = eiα eiβ .
In ogni caso, tenuto conto della (2) e posto w = R(cos φ + i sin φ), la (1)
diviene
ρn (cos nθ + i sin nθ) = R(cos φ + i sin φ),
(3)
dalla quale si ricava
ρ=
√
n
R,
nθ = φ + 2kπ.
In altre parole le soluzioni della (1) o equivalentemente della (3) sono tutti i
numeri z esprimibili come
√
n
z = R(cos θ + i sin θ),
dove
θ=
φ + 2kπ
,
n
2
per qualche intero k. Apparentemente al variare di k sui numeri interi si
presentano infinite soluzioni perché sono infiniti i possibili valori di θ. Tuttavia è facile convincersi che se k varia su n valori consecutivi, ad esempio
k = 0, 1, . . . n − 1 si esauriscono i valori di θ che danno luogo a valori diversi
di cos θ + i sin θ. Possiamo quindi identificare n soluzioni diverse della (1) e
precisamente, per k = 0, . . . , n − 1,
zk =
√
n
R(cos
φ + 2kπ
φ + 2kπ
+ i sin
).
n
n
In particolare, se n = 2, se cioè siamo interessati alle radici quadrate del
numero w = R(cos φ + i sin φ), avremo le due soluzioni
√
√
z1 = R(cos φ/2 + i sin φ/2), e z2 = R(cos(φ/2 + π) + i(sin(φ/2 + π)).
Si può osservare a questo punto che z1 = −z2 , in quanto
eiφ/2+π = eiφ/2 eiπ = −eiφ/2 .
Esercizio 2 Trovare tutte le soluzioni delle seguenti equazioni:
z 2 = i, z 3 = −1, z 2 = 2 − 2i,
√
z 4 = 1 + i 3, z 2 = 1 z 3 = 1, z 4 = 1,
z 8 = 1.
L’esistenza di n radici n-esime di ogni numero complesso diverso da zero
si applica naturalmente anche alle radici quadrate. Questo ci permette di
verificare che la formula risolutiva per le equazioni di secondo grado continua
a valere anche quando si tratta di un’equazione a coefficienti complessi. In
altre parole possiamo considerare l’equazione
z 2 + βz + γ = 0,
(4)
dove β e γ sono numeri complessi, e verificare che le soluzioni sono fornite
dalla formula
p
−β + β 2 − 4γ
.
(5)
z=
2
Si parla di due soluzioni perché le radici quadrate di un numero complesso,
2
diverso da zero
p sono due, una opposta dell’altra. Pertanto, se β − 4γ 6= 0
2
l’espressione β − 4γ corrisponde a due valori distinti. (Ricordiamo che
nel caso di equazioni a coeffienti reali questi due valori erano indicati esplici√
tamente con il simbolo ±, perché in ambito reale il simbolo . viene usato
per indicare la radice quadrata non negativa di un numero non negativo)
3
Esercizio 3 Trovare le soluzioni delle seguenti equazioni
z 2 + 3iz + 4 = 0,
z 2 + 2z + 1 − i = 0,
z 2 + (1 + i)z + i = 0.
Esercizio 4 Dimostrare che se il polinomio
p(z) = z n + an−1 z n−1 + · · · + a0 ,
ha coefficienti reali, ed il numero complesso α è una radice del polinomioo
(cioè p(α) = 0) allora anche il numero coniugato α è una radice dello stesso
polinomio.
2
Una giustificazione sommaria della formula
di Eulero
La formula di Eulero
eit = cos t + i sin t,
può essere considerata come una forma suggestiva per indicare l’espressione
cos t + i sin t,
giustificabile solo dal fatto che le formule di addizione di sin t e di cos t
dimostrano che
eit eis = (cos t + i sin t)(cos s + i sin s) = cos(s + t) + i sin(s + t) = ei(s+t) .
Nelle righe che seguono senza alcuna pretesa di completezza cercheremo di
dare una giustificazione diretta della formula di Eulero.
Partiamo dalle espressioni di sin t e cos t come serie di potenze, cioè come
limiti dei corrispondenti polinomi di Taylor di punto iniziale 0. Queste sono:
cos t =
e
∞
X
t2k
,
(−1)k
(2k)!
k=0
∞
X
sin t =
(−1)k
k=0
t2k+1
(2k + 1)!
Consideriamo ora i numeri complessi
zn =
n
X
(it)k
k=0
4
k!
,
e osserviamo che ik assume solo quattro valori: il valore 1 quando k è un
multiplo di 4, il valore −1 quando k è pari, ma non è un multiplo di 4, il
valore i quando k è ottenuto da un multiplo di 4 aggiungendo uno, ed infine
il valore −i quando k è ottenuto da un multiplo di 4 aggiungendo 3. Ne segue
che (it)k = ik tk assume valori reali ±tk quando k è pari e valori immaginari
±itk quando k è dispari, pertanto raccogliendo i termini reali ed i termini
immaginari possiamo scrivere
z2n =
n−1
n
X
X
t2k+1
t2k
+i
(−1)k
.
(−1)k
(2k)!
(2k
+
1)!
k=0
k=0
Questo significa che la parte reale di z2n è il polinomio di Taylor di ordine
2n di cos t e la parte immaginaria di z2n è il polinomio di Taylor di ordine
2n − 1 di sin t. Poiché l’espressione del resto nella forma di Lagrange ci
assicura che per ogni t reale i polinomi di Taylor di cos t e sin t convergono
alle rispettive funzioni, possiamo concludere che la parte reale di z2n converge
a cos t e la parte immaginaria di z2n converge a sin t. Questo ci autorizza a
dire che la successione di numeri complessi z2n converge al numero complesso
cos t+i sin t. Non è difficile convincersi che lo stesso ragionamento vale per la
successione zn , indipendentemente dalla parità di n. Una notazione coerente
per il limn zn è la serie
∞
X
(it)k
= eit .
k!
k=0
A questo punto possiamo scrivere:
∞
X
(it)k
k=0
k!
=
∞
∞
X
X
t2k
t2k+1
(−1)k
+i
(−1)k
(2k)!
(2k + 1)!
k=0
k=0
Ne segue la formula di Eulero se, come è naturale, attribuiamo il valore
e al primo membro di questa uguaglianza.
it
5