ah-1 ATOMI IDROGENOIDI • Si tratta di atomi con un solo elettrone

ah-1
Università di Roma “ La Sapienza”
ATOMI IDROGENOIDI
•
Si tratta di atomi con un solo elettrone ed un
nucleo di carica positiva Z e
•
Dobbiamo impostare e risolvere l’equazione di
Schroedinger per questo sistema di due particelle
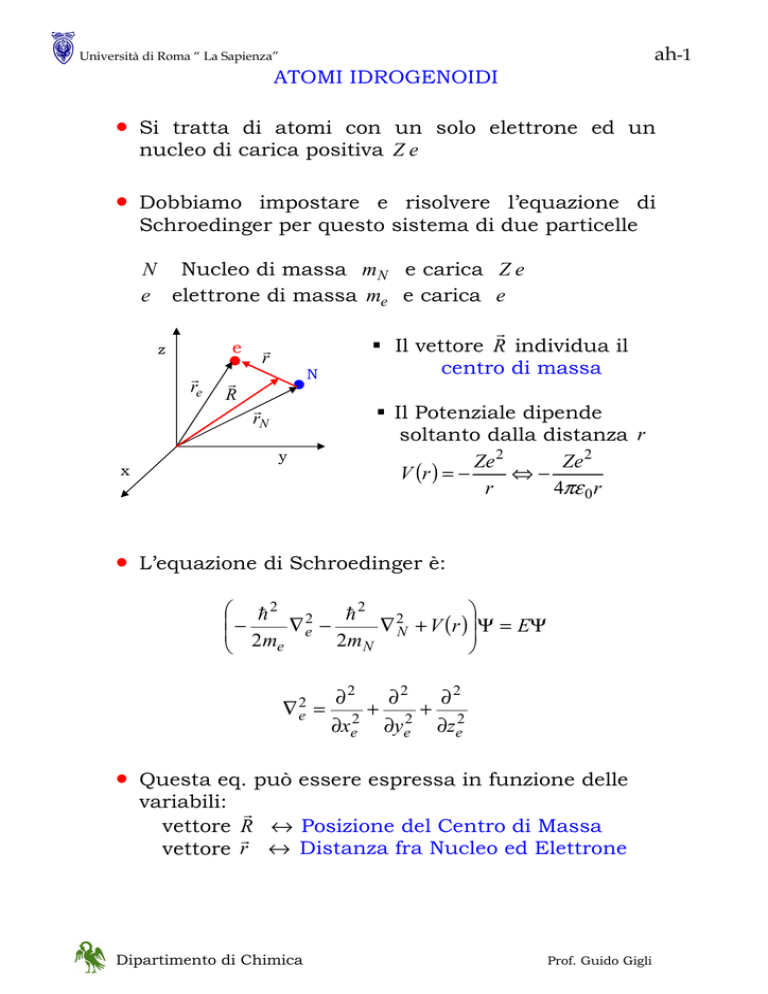
N Nucleo di massa mN e carica Z e
e elettrone di massa me e carica e
e
z
r
re
x
•
r
R
r
r
r
ƒ Il vettore R individua il
centro di massa
N
r
rN
ƒ Il Potenziale dipende
soltanto dalla distanza r
Ze 2
Ze 2
⇔−
V (r ) = −
r
4πε 0 r
y
L’equazione di Schroedinger è:
2
 h2 2

h
2
−
Ψ = EΨ
∇
−
∇
+
V
(
r
)
N
 2 m e 2m

e
N


∇ e2
•
=
∂2
∂xe2
+
∂2
∂ye2
+
∂2
∂ze2
Questa eq. può essere espressa in funzione delle
variabili: r
vettore R ↔ Posizione del Centro di Massa
r
vettore r ↔ Distanza fra Nucleo ed Elettrone
Dipartimento di Chimica
Prof. Guido Gigli
ah-2
Università di Roma “ La Sapienza”
si ottiene, per via classica, un Hamiltoniano
2
2
h
h
2
r
Hˆ = −
∇R −
∇r2r + V (r ) che tiene conto di:
2M
2µ
- energia cinetica dell’intera massa del sistema
pari ad M = mN + me
- energia cinetica ed energia potenziale della
particella fittizia di massa ridotta µ
mm
µ= e N
me + mN
SE V (r ) ≠ f (t )
r r
r r
Hˆ Ψ (R, r ) = E Ψ (R, r )
Si separa facilmente
con Ψ ( R, r ) = χ ( R ) ⋅ Ψ (r )
( R ed r sarebbero sempre vettori )
h2 2
−
∇ R χ ( R ) = Er χ ( R )
2M
 h2 2

−
∇
+
V
(
r
)

 Ψ (r ) = Er Ψ (r )
r
2
µ


Traslazione libera di
una particella di
massa M
Eq. di Schroedinger
per una particella
fittizia di massa µ che
si muove in un
potenziale V(r)
IN SINTESI
Abbiamo ottenuto un risultato della
massima importanza che, in generale,mostra
che il moto traslazionale può essere separato
ESATTAMENTE dai moti cosiddetti “interni”
Dipartimento di Chimica
Prof. Guido Gigli
ah-3
Università di Roma “ La Sapienza”
•
Per quanto riguarda l’energia
ETotale = ETraslazione
•
+
EMoti Interni
Dal punto di vista fisico, e per quanto riguarda i
moti interni, tutto ciò equivale a considerare il
nucleo pressochè fermo e l’elettrone in moto
rispetto a questo
INFATTI
mN >> me
⇒
mN ≅ 1800 me
µ≅
1800 ⋅ me 1800 ⋅ me
=
≈ me
1800 + 1
1801
a parità di tempo
elettrone 1000 A
µ ≅ me
poichè
o
nucleo
•
o
0.1 A
Procediamo ora nella soluzione della eq.
Schroedinger della particella µ nel potenziale
V (r ) ↔ Potenziale Centrale
usando le coordinate polari
∇ r2 =
1 ∂  2 ∂  1
r
 + 2
2 ∂r 
r
 ∂r r
di
 1
∂ 
∂ 
∂ 
1
θ
sen
+



2
2
θ
θ
θ
∂
∂
sen


sen
θ
∂
φ


CIOE’ ( vedi rr-5 )
∇ 2r =
1 ∂  2 ∂  1 1 ˆ2
 r
 −
L
r 2 ∂ r  ∂ r  r 2 h2
Dipartimento di Chimica
Prof. Guido Gigli
ah-4
Università di Roma “ La Sapienza”
Hˆ = −
h2
∂  2 ∂ 
1 ˆ2


r
+
L + V (r ) =


2µ r 2 ∂ r  ∂ r  2µ r 2
Tˆ (r )
=
•
f (r ) Lˆ2 + V (r )
+
Osserviamo che
[
]
♦ Hˆ , Lˆ 2 = 0
INFATTI
[Τˆ (r ) + f (r ) Lˆ + V (r ) , Lˆ ] = [Τˆ (r ), Lˆ ]+ [ f (r ) Lˆ , Lˆ ]+ [V (r ), Lˆ ]
[Τˆ (r ), Lˆ ] = 0 i due operatori dipendono da variabili diverse
[V (r ), Lˆ ] = 0
[ f (r ) Lˆ , Lˆ ] = [ f (r ), Lˆ ]⋅ Lˆ + f (r )[Lˆ , Lˆ ] = 0
2
2
2
2
2
2
2
2
2
2
2
2
2
2
a
b
a) i due operatori dipendono da variabili diverse
b) un operatore commuta sempre con se stesso
♦ L̂z commuta con Lˆ 2
L̂z non dipende da r
[Lˆ
2
]
, Lˆ z = 0
QUINDI
[Hˆ , Lˆz ]= 0
Gli operatori Hˆ , Lˆ 2 ed Lˆ z hanno
autofunzioni in comune
Dipartimento di Chimica
Prof. Guido Gigli
ah-5
Università di Roma “ La Sapienza”
•
Le autofunzioni di L̂ 2 ed L̂z (che non operano su r )
sono le armoniche sferiche Yl , m (θ , Φ )
ogni funzione del tipo R(r )Yl m (θ , Φ )
è ancora autofunzione
QUINDI
Hˆ Ψ (r ,θ , φ ) = E Ψ (r ,θ , φ )
Lˆ 2 Ψ (r ,θ , φ ) = l (l + 1) h 2 Ψ (r ,θ , φ )
Lˆ z Ψ (r ,θ , φ ) = m h Ψ (r ,θ , φ )
Ψ (r ,θ , φ ) = R (r )Yl , m (θ , φ )
che sostituita nella eq. di Schroedinger
e dividendo per Ψ consente di scrivere


1 ˆ2
ˆ
T
r
L
V
r
(
)
+
+
(
)

 R (r )Yl , m (θ , φ ) = E
2
R (r )Yl , m (θ , φ ) 
2µ r

Tˆ (r ) R (r )
1
2
+
l
(
l
+
1
)
h
+ V (r ) = E
2
R (r )
2µ r
1
 h 2
−
 2 µ r 2
 
 d  2 d   h 2

(
)
(
)

1
r
l
l
V
r
+
+
+
  R(r ) = E R (r )
 
 
2
d
r
d
r
  2 µ r
 
 
Vˆeff
Hˆ e
Dipartimento di Chimica
Prof. Guido Gigli
ah-6
Università di Roma “ La Sapienza”
•
Notiamo che:
‰
Ĥ dipende dal numero quantico l
ci aspettiamo che anche le soluzioni R(r )
dipendano da l
‰
‰
‰
Al potenziale centrale V (r ) che, nel nostro caso è
attrattivo, si somma un termine repulsivo che può
essere interpretato come dovuto ad effetti
centrifughi ( l ≠ 0 )
Sino ad ora la trattazione è generale nel senso di
essere applicabile a tutti i casi di due corpi
interagenti ( p.e. V(r) potrebbe essere il potenziale
di interazione fra due atomi in una molecola )
Per il caso dell’atomo Idrogenoide
Ze 2
V (r ) = −
µ ≅ me = m
r
•
La soluzione della eq. Hˆ e R (r ) = E R (r ) è, come
spesso accade, piuttosto difficile; ne vedremo
soltanto i risultati ma prima di cio’ introduciamo
delle unità di misura assai usate in chimica
quantistica: le unità atomiche
•
Si tratta di unità di misura che consentono di
ottenere espressioni analitiche piu’ semplici ed
aver a che fare con numeri dell’ordine di grandezza
dell’unità
Dipartimento di Chimica
Prof. Guido Gigli
ah-7
Università di Roma “ La Sapienza”
Lunghezza
o
h2
−10
=
0
.
52918
A
=
0
.
52918
⋅
10
m
a0 =
2
me
( se µ = me )
BOHR ( raggio della I orbita dell’atomo di Bohr)
massa
tempo
carica
energia
me = 1 u.a. = 9.10 ⋅ 10 − 28 g = 9.10 ⋅ 10 − 31 Kg
τ0 =
a0 h
e2
= 2.4189 ⋅10 −17 s
tempo impiegato da 1 elettrone
1s dell’atomo di H per percorrere
1 bohr
e = 1,602189 ⋅10 −19 C
carica dell’elettrone
e2
= 1 Hartree = −2 ⋅ ( ETOT di un elettrone 1s )
a0
= - 2 13.606 eV = 27.212 eV
momento angolare
Campo elettrico
h
e
a02
campo elettrico di un protone alla
distanza di 1 bohr
QUINDI
Per esempio, con queste unità, l’Hamiltoniano
dell’atomo idrogenoide ( con µ = µε ) diventa:
h2
Z e2
2
ˆ
∇ −
H = −
2 me
r
Dipartimento di Chimica
Z
1
Hˆ = − ∇ 2 −
2
r
Prof. Guido Gigli
ah-8
Università di Roma “ La Sapienza”
Autofunzioni
l
 Zr   2rZ 
 2r Z 
 ⋅ 
 ⋅ L2nl++l1

Rnl (r ) = N ⋅ exp −
na
na
n
a

0 
0
0 

( L2nl++l1 sono funzioni complicate dette polinomi associati di
Laguerre ed N è un fattore di normalizzazione)
complessivamente, quindi, si ha:
Ψnlm = Rnl (r )Ylm (θ , φ )
12
Ψnlm
 2 Z 3 (n − l − 1) ! 


= − 
3
n
a

0  2 n [(n + l ) !] 

⋅
l
 Zr   2rZ 
 2r Z 
 ⋅ 
 ⋅ L2nl++l1
 ⋅ Yl ,m (θ , φ )
exp −
 na 0   na 0 
 n a0 
Ψnlm = n, l , m = n, l , ml
per gli elettroni si usa ml
•
•
Come si vede dall’equazione differenziale che si era
ottenuta, per ogni valore del numero quantico l ci
sono infinti valori di n che soddisfano tutte le
condizioni fisiche volute; si dimostra che n puo’
assumere soltanto i valori l+1, l+2, ..ecc.
Complessivamente
i
numeri
quantici
che
compaiono nelle autofunzioni possono assumere
soltanto alcuni valori e sono fra loro correlati
n = 1, 2, 3,...
l = 0, 1, 2…(n-1)
ml = 0,
± 1, ± 2
Dipartimento di Chimica
numero quantico principale
“
±l “
“
“
orbitale od
azimutale
magnetico
Prof. Guido Gigli
ah-9
Università di Roma “ La Sapienza”
•
Sostituendo i vari valori di n , l , ml si ha:
32
Ψ1,0,0
1 Z 
 
=
π  a0 
Ψ2,0,0
1
=
4 2π
Z 
 
 a0 
Ψ2,1,0
1
=
4 2π
Z 
 
 a0 
Ψ2,1,±1
1 Z 
 
=
8 π  a0 
 Z r

exp −
a

0 
32

 Zr
Z r
 2 −
 exp −

a
2
a


0 
0
32
 Zr
Zr
 cos θ
exp −
a0
2
a

0
32
 Zr
Zr
 senθ exp(± iφ )
exp −
a0
2
a

0
Z 
 
 a0 
Ψ3,0,0
1
=
81 3π
Ψ3,1,0
2 Z 
 
=
81 π  a0 
32
32
Z 
 
 a0 
1
=
81 6π
Z 
 
 a0 
1
Ψ3,2,±1 =
81 π
Z 
 
 a0 
Ψ3, 2,0
Ψ3,2,±2
•

 Z r
Z rZ r
 6 −

 cos θ
exp −
a0  a0

 3a0 
32
1
Ψ3,1,±1 =
81 π
2 2

 27 − 18 Z r + 2 Z r  exp − Z r 
 3a 

a0
a0 2 

0


 Z r
Z rZ r
 6 −

 senθ exp(± iφ )
exp −
a0  a0

 3a0 
32
 Z r
Z 2 r2
 3 cos 2 θ − 1
exp −
a0
 3a0 
32
 Z r
Z 2 r2
 senθ cos θ exp(± iφ )
exp −
a0
3
a

0
1 Z 
 
=
162 π  a0 
(
32
)
 Z r 2
Z 2 r2
 sen θ exp(± 2iφ )
exp −
a0
3
a

0
Da notare che la parte in r è del tipo
(
)
Rn ,l (r ) = costante ⋅ r l Polinomio r n −l −1 ⋅ exp ( −
Dipartimento di Chimica
Zr
)
n
Prof. Guido Gigli
ah-10
nella funzione Rn,l(r) compare, quindi, un polinomio
in r di grado n-1 con piu’ o meno termini a seconda
del valore di l.
• Le funzioni radiali sono normalizzate:
∞ 2 2
∫0 R r dr = 1
Università di Roma “ La Sapienza”
dove è importante notare che si è usata la parte in r
dell’elemento di volume in coordinate polari:
r 2 sen θ dθ dφ dr
Autovalori
Gli autovalori dell’energia dipendono dal solo numero
quantico n
En = −
m Z 2 e4
2 n 2 h2
Z 2 e2
=− 2⋅
2n a 0
En = −
Z2
2n 2
Poichè l’energia dipende soltanto da “ n ” ma vi sono
vari valori di “ l ” ed “ m ” per ogni valore di “ n ” ogni
stato del sistema è degenere
g n = n 2 =1 + 3 + 5 + 7... + (2n − 1)
∗
l
Infatti:
m = 2(l + 1)
oppure:
n
6444447
444448
(n ∗ − 1)
0 1 2 3 K
M M M M
1 3 5 7 K 2 (n ∗ − 1) + 1
 n(n − 1)
2
2
+
n
=
n
−
n
+
n
=
n
∑ (2l + 1) = 2 ∑ l + n = 2

n −1
n −1
l =0
l =0

2

La notazione è la seguente
l
simbolo
0
s
sharp
Dipartimento di Chimica
1
2
p
d
principal diffuse
3
f
fundamental
Prof. Guido Gigli
ah-11
Università di Roma “ La Sapienza”
•
Vediamo l’andamento della parte radiale delle
autofunzioni
Il numero di
“nodi” e’ pari
ad n -l -1
•
E’ utile analizzare la probabilità di trovare
l’elettrone ad una distanza r dal nucleo; ossia in
una corteccia sferica di spessore dr
2
Ψ integrata su tutti gli angoli =
π 2π *
∫0 ∫0 Ψnlm (r ,θ , φ )Ψnlm (r ,θ , φ )drdθdφ =
π 2π
2
*
Rnl
(r )r 2 dr ∫0 ∫0 Ylm
Ylm sen θ dθ dφ =
2
Rnl
(r ) r 2 dr ⋅ 1 ( le armoniche sferiche sono normalizzate )
•
si ha, quindi, la funzione di distribuzione radiale
P (r ) dr =
R 2r 2
dr
A parita’ di n la
probabilita’ di
trovare un
elettrone vicino al
nucleo diminuisce
con l
Dipartimento di Chimica
Prof. Guido Gigli
ah-12
Università di Roma “ La Sapienza”
•
da notare che per l’orbitale 1s la distanza a cui si
ha massima probabilita’ di trovare l’elettrone (rprob)
e’ proprio in corrispondenza del raggio di Bohr
• è anche istruttivo valutare la distanza media
dell’elettrone dal nucleo
r = Ψnlm r Ψnlm = Rnl (r )Ylm (θ ,φ ) r Rnl (r )Ylm (θ ,φ ) =
∞ π 2π
*
2
∫0 ∫0 ∫0 R Y r R Y r senθ dr dθ dφ =
∞ 2 3
π 2π
∞ 2 3
*
∫0 R r dr ∫0 ∫0 Y Y senθ dθ dφ = ∫0 R r dr =
n 2  3 l (l + 1) 
a0
−
Z  2 2 n 2 
dove si puo’ notare che
- per Z=1, n=1, l=0 ( cioè per lo 1s di H ) rmedio = 1.5
a0
- all’umentare di Z diminuisce rmedio
- rmedio(2s) ≠ rmedio(2p) anche se i due orbitali sono
degeneri ( come mai?)
rprob
rmedio
• Consideriamo ora anche la parte angolare
ƒ per
l =0
la simmetria è sferica sia per Ψ
che Ψ
Dipartimento di Chimica
2
Prof. Guido Gigli
ah-13
Università di Roma “ La Sapienza”
ƒ per
l≠0
si devono considerare le forme
delle armoniche sferiche
e
della “deformazione” delle stesse
dovuta alla parte radiale
vediamo il solo caso
degli ORBITALI p
termine dovuto a
Mulliken che
ricorda le orbite
dell’atomo di Bohr
 Zr 
 ⋅ cosθ
Ψ2,1,0 = Ψ2 p 0 = Ψ2 pz = cost ⋅ r ⋅ exp  −
 2 a0 
per la sola
parte angolare
Dipartimento di Chimica
Prof. Guido Gigli
ah-14
Università di Roma “ La Sapienza”
• Comunque quella che interessa di più è la intera
Ψ
che si rappresenta bene con “curve di livello” le
quali uniscono i punti nei quali la funzione assume
il medesimo valore o modulo
Ψ
2
Ψ2 p ±1
• Si tratta di funzioni immaginarie
 Zr 

cos t ⋅ r ⋅ exp  −
2
a

0
senθ
e± iφ
Peraltro
Ψ2* p +1 = Ψ2 p −1
Ψ2* p +1 Ψ2 p +1 = Ψ2 p −1 Ψ2 p +1
=
Ψ2* p −1 Ψ2 p −1 = Ψ2 p +1 Ψ2 p −1
Dipartimento di Chimica
Ψ2* p −1 = Ψ2 p +1
i due orbitali Ψ2 p ±1
hanno la medesima
funzione densita’ di
probabilità
Prof. Guido Gigli
ah-15
Università di Roma “ La Sapienza”
INOLTRE
Ψ2 p +1 e Ψ2 p −1
anche una loro combinazione
lineare è autofunzione di
Ĥ con lo stesso autovalore
sono degeneri
per rappresentarle usiamo una combinazione
lineare che sia reale
(
1
Ψ2 p + 1 + Ψ2 p −1
2
)
1
senθ
2
= R(r )2 p ± 1
= R(r )2 p ± 1
Ψ2 px = cost ⋅ r
x = r
1
senθ
2
( ei φ + e − i φ ) =
2 cos Φ
 Zr 
 senθ cos Φ
exp  −
2
a
0

senθ cos Φ
Analogamente
1
i
(Ψ2 p +1 − Ψ2 p −1 ) = Ψ2 py = cost
2
y
 Zr 
 senθ sen Φ
exp  −
2
a
0

r
=
r
sen θ senΦ
• Analoghe combinazioni lineari di autofunzioni
degeneri con termini immaginari le rendono reali
(orbitali d, f, ecc )
• Possiamo, peraltro, notare che queste nuove
funzioni d’onda non rappresentano più autostati di
L̂ z (anche se sono ancora autostati di Ĥ ed L̂2 )
Dipartimento di Chimica
Prof. Guido Gigli
ah-16
Università di Roma “ La Sapienza”
En = −
m Z 2e 4
2 h 2n2
per l’Idrogeno
(Z = 1) :⇒ En = −
m e4
2 h 2n2
quindi per l’atomo di Idrogeno:
En cm
−1
=−
se µ = me
me 4
4 π h 3c n 2
=−
Costante di Rydberg
= 109737 cm-1
R∞
n2
mN = ∞
R∞
me mH
m N = m H RH
me + mH
Vi è un addensamento di livelli all’aumentare del
numero quantico “n”
se µ =
E’ interessante osservare l’andamento dei livelli per
vari tipi di potenziale
Si nota la competizione fra due effetti
Aumento
dell’intervallo fra i
livelli
all’aumentare
dell’Energia
Dipartimento di Chimica
Diminuzione della
spaziatura fra i livelli
all’aumentare delle
dimensioni spaziali nelle
quali è confinata la
particella
Prof. Guido Gigli
ah-17
Università di Roma “ La Sapienza”
• Per avere una ulteriore idea della scala delle energie
permesse rispetto al potenziale si può sovrapporre
all’andamento del potenziale sresso i livelli della
espressione E = − R n 2
• Ogni livello è, come già detto, degenere ( n 2 ) così
come indicato nella ordinata di destra
Dipartimento di Chimica
Prof. Guido Gigli
ah-18
Università di Roma “ La Sapienza”
• Per rappresentare questa degenerazione
( per
quanto riguarda il numero quantico “l” ) si possono
rappresentare i livelli degeneri in posizioni
adiacenti:
con le opportune Regole di
Selezione si possono
indicare le transizioni in
un Diagramma di Grotrian
∆n = qualsiasi
∆l = ±1
∆ml = 0,±1
da notare che è un valore diverso dalla R∞ = 109737 cm
−1
• E’ importante osservare che esistono anche
soluzioni al nostro Hamiltoniano, ( complesse da
trovare ), con
E>0
che non sono quantizzate
Stati non legati
continuo di Energia
(oltre la Ionizzazione )
Le autofunzioni corrispondenti sono
fondamentali nello studio di
Collisione elettrone ione
fenomeni di “scattering”
Dipartimento di Chimica
Prof. Guido Gigli
ah-19
Università di Roma “ La Sapienza”
•
Terminiamo la trattazione con due osservazioni su:
Caratteristiche degli orbitali
ƒ
Tutti gli orbitali con l = 0 hanno valore finito sul
nucleo
“
“
l≠0 “
“ nullo “
“
la forma dello 1 s può
essere considerata un
compromesso
fra
Ψ
V
- Bassa Ecin
r
piccola curvatura di Ψ
- Bassa V
grande energia cinetica
ƒ Negli atomi Idrogenoidi all’aumentare di Z la distanza
di massima probabilità diminuisce
La carica più grande attira verso il nucleo
l’elettrone
Energia degli orbitali
• L’energia dipende dal numero atomico Z
QUINDI
E’ sempre più in basso in energia
( aumenta in modulo)
all’aumentare di Z
per lo He+ è quattro
volte piu’ grande
Dipartimento di Chimica
Prof. Guido Gigli
ah-20
Università di Roma “ La Sapienza”
Ulteriori Complicazioni
• Abbiamo visto che siamo in grado di spiegare lo
spettro di un atomo di Idrogeno
Se si applica un campo magnetico la degenerazione
degli stati di moto con il medesimo l e diverso m
viene rimossa
ƒ Mettiamo in evidenza la
quantizzazione spaziale
ƒ Ci aspettiamo 3
transizioni
Questo lo possiamo spiegare perchè all’elettrone in
moto è associato un momento magnetico che
interagisce con il campo magnetico esterno
• Se, però,si usa un campo magnetico molto forte e
si osserva lo spettro con grande risoluzione non si
riesce a spiegare la comparsa di 6 transizioni che
generano 5
righe spettrali
struttura
FINE
• Un altro esperimento di natura completamente
diversa, impone di considerare qualcosa d’altro
STERN GERLACH (già visto nei lucidi “in”)
Dipartimento di Chimica
Prof. Guido Gigli
ah-21
Università di Roma “ La Sapienza”
• Il nuovo concetto che deve essere introdotto per
spiegare la struttura fine è lo SPIN
E’ cosa del tutto nuova e non vi sono analogie
classiche
ƒ Di conseguenza non si può procedere nel modo
usuale:
Esprimere la grandezza classica in funzione di
momenti e coordinate
Sostituire questi momenti e coordinate con gli
operatori appropriati
ƒ Si deve procedere introducendo altri postulati
quantomeccanici ( in realtà nella formulazione
relativistica di DIRAC lo SPIN
compare naturalmente)
I ) Gli operatori del momento angolare di Spin
commutano e si combinano come gli operatori del
momento angolare normale
Sˆ 2 Sˆ z − Sˆ z Sˆ 2 = 0
ecc
Sˆ x Sˆ y − Sˆ y Sˆ x = i h Sˆ z
ecc
Dipartimento di Chimica
Prof. Guido Gigli
ah-22
Università di Roma “ La Sapienza”
II ) Vi sono soltanto due autofunzioni ( α e β ) degli
operatori di momento angolare di spin.
Gli autovalori corrispondenti sono:
Sˆ 2 α = s ( s + 1) h 2 α
Sˆ 2 β = s ( s + 1) h 2 β
s =1 2
r
S = 3 4h
Sˆ z α = m s h α = 1 2 h α
ms = ± 1 2
ˆ
S z β = ms h β = −1 2 h β
per la notazione:
α e β ⇒ s, ms
α = 1 2 ,1 2 = ↑
β = 1 2, −1 2 = ↓
N.B. La parte difficile è che queste funzioni α e β sono
funzioni del tutto astratte di uno spazio anch’esso
astratto.
Si può generalizzare:
ƒ L’entità del momento angolare di spin di una
particella è determinato dal numero quantico di
spin
ƒ questo numero quantico ha un UNICO valore
positivo (intero o semintero ) che è caratteristico
della particella (per esempio:
s= 3
non s = 0, 1 ,1, 3 )
2
2
2
ƒ ( anche ad ogni nucleo e’ associato uno spin
caratteristico )
ƒ La distinzione fra particelle con spin intero
( BOSONI ) e particelle con spin semintero
(FERMIONI ) è di tipo fondamentale
Seguono forme diverse del principio di
esclusione di PAULI
Dipartimento di Chimica
Prof. Guido Gigli
ah-23
Università di Roma “ La Sapienza”
•
Da quanto detto si evince che l’orientazione del
momento angolare di spin è quantizzata
Sz/h
s =1/2
r
3
S =
h
2
III ) L’elettrone ( con spin) agisce come un piccolo
magnete il cui momento di dipolo è:
r
µ = g s × (momento angolare di spin)×
−e
2 me c
- Il fattore g s è postulato essere pari a due volte il
fattore classico. In realtà g s =2.0023227 ; valore
previsto dalle teorie moderne di elettrodinamica
quantistica
-
gs
−e
= γ → Rapporto giromagnetico dell' elettrone
2 me c
Una finzione relativa allo spin è:
Lo spin è il momento angolare che consegue alla
rotazione di un corpo intorno al proprio asse
Le particelle cariche con spin possiedono un
momento magnetico intrinseco
Dipartimento di Chimica
Prof. Guido Gigli
ah-24
Università di Roma “ La Sapienza”
•
Da quanto si è visto emerge che l’elettrone
dell’atomo idrogenoide possiede sia un momento
angolare orbitale che un momento angolare di spin
r
l = l (l + 1) h
r
s = s (s + 1) h
l z = ml h
•
s z = ms h
I contributi di questi due momenti angolari elettronici si
combinano per fornire un momento angolare elettronico
totale
r
j
r
= l
+
r
s
Per analogia con i casi precedenti:
r
j =
jz = m j h
j
( j + 1)
h
m j = − j,− j + 1, K + j
r
j
•
Vediamo i possibili valori di
r
r
di l e di s
•
r
r
Consideriamo le componenti di l e di s
per valori particolari
l z = −l h , (− l + 1) h,.........,+l h
1
1
s z = − h, + h
2
2
la componente j z sarà la somma delle componenti
l z ed s z considerando tutte le somme possibili
Dipartimento di Chimica
Prof. Guido Gigli
ah-25
Università di Roma “ La Sapienza”
•
Per esempio :
con
l =1
(
s =1 2
→
l z = −1 h
)
s z = −1 2 h
si ha per j z → j z h =
•
−
3
1
−
2
2
+ 1h
0
+1 2h
−
1 1
2 2
1
2
3
2
1
1
deriva da j =
lo stato j z = h
2
2
1
1 1
mj = −
ma per j =
2
2 2
3
3
deriva da j =
lo stato j z = h
2
2
3
3
1
1
3
mj = −
−
ma per j =
2
2
2
2
2
Allo stesso risultato ( quando c’è un solo elettrone
) si perviene sommando e sottraendo l ed s
per qualsiasi valore di
1
di l ≠ 0 si hanno due
2
valori di j
j =l+s=3 2
j = l − s =1 2
Si può generalizzare questa considerazione :
l =1
s=
♦ Quando vi sono due momenti angolari ( con
numeri quantici j1 e j2 ) anche il momento
angolare totale è quantizzato ( con modulo
[J ( J + 1)] 1 2 h ) ed il numero quantico J è fornito
dai termini della cosiddetta serie di ClebschGordan
J = ( j1 + j2 ), ( j1 + j2 ) − 1, K, j1 − j2
•
Nel nostro esempio un elettrone p (l = 1) dà luogo a
due stati di moto con diverso momento angolare
totale
Dipartimento di Chimica
Prof. Guido Gigli
ah-26
Università di Roma “ La Sapienza”
•
•
Questi stati con diverso momento elettronico
angolare totale hanno energia diversa
L’origine
della
differenza
in
energia
è
l’accoppiamento SPIN-ORBITA che nasce dalla
interazione fra i momenti magnetici associati ai
momenti angolari orbitali e di spin
per una descrizione quantitativamente
corretta di queste interazioni è necessaria
una
trattazione
quantomeccanica
relativistica ( Dirac 1928 )
•
Non è più sufficiente specificare con un simbolo la
configurazione (1s,2 s,2 p..... ) e,quindi
2 S +1
2 S +1
Lj
specifica il
L
termine
2 S +1
dove per l = 0 1 2 3
L = S P D FK
•
specifica il livello
LJ
Ne consegue che per un atomo di Idrogeno si
hanno i livelli seguenti
configurazione → n s
livello
→ 2 S1 2
2
P1 2 2 P3 2
np
2
D3 2 2 D5 2
nd
2
nf
F5 2 2 F7 2
ogni livello è 2J+1 volte degenere (ad ogni livello
corrispondono 2J+1 stati )
•
una notazione completa è, per esempio: 2 p 2 P1 2
Dipartimento di Chimica
Prof. Guido Gigli
ah-27
Università di Roma “ La Sapienza”
•
Il diagramma dei livelli energetici va, quindi,
modificato inserendo lo splittamento dei livelli con
diverso j
•
Ci si deve attendere che per uno stesso termine
2 s +1
L il livello con j più piccolo sia ad energia
minore perchè i momenti magnetici orbitale e di
spin si accoppiano in modo attrattivo
jz = l z − sz
•
jz = lz + sz
Il risultato è il seguente diagramma di Grotrian:
(da notare che lo “splitting” j diminuisce
all’aumentare di ‘n’ e di ‘l’ )
Dipartimento di Chimica
Prof. Guido Gigli