Circuiti con un solo generatore di tensione - Digilander

Circuiti con un solo generatore di tensione – esercizio n. 3
riduzione del circuito ad una sola resistenza
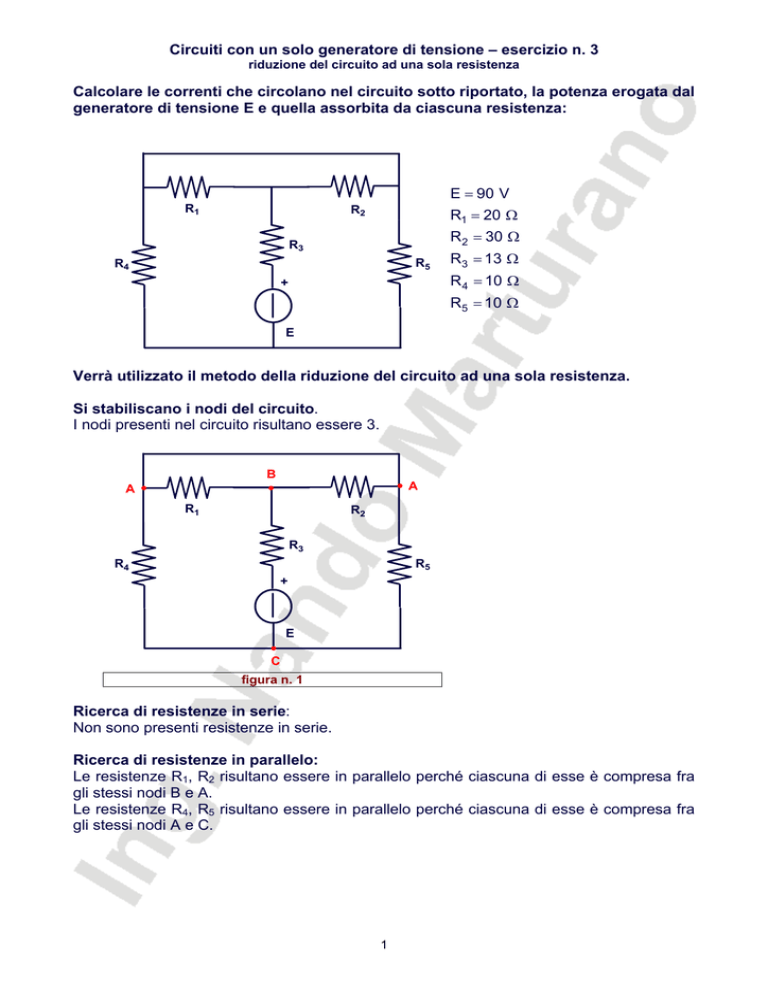
Calcolare le correnti che circolano nel circuito sotto riportato, la potenza erogata dal
generatore di tensione E e quella assorbita da ciascuna resistenza:
R1
E = 90 V
R1 = 20 Ω
R2
R2 = 30 Ω
R3
R5
R4
R3 = 13 Ω
R 4 = 10 Ω
+
R5 = 10 Ω
E
Verrà utilizzato il metodo della riduzione del circuito ad una sola resistenza.
Si stabiliscano i nodi del circuito.
I nodi presenti nel circuito risultano essere 3.
B
A
A
R1
R2
R3
R5
R4
+
E
C
figura n. 1
Ricerca di resistenze in serie:
Non sono presenti resistenze in serie.
Ricerca di resistenze in parallelo:
Le resistenze R1, R2 risultano essere in parallelo perché ciascuna di esse è compresa fra
gli stessi nodi B e A.
Le resistenze R4, R5 risultano essere in parallelo perché ciascuna di esse è compresa fra
gli stessi nodi A e C.
1
Circuiti con un solo generatore di tensione – esercizio n. 3
riduzione del circuito ad una sola resistenza
Calcolo della resistenze equivalenti;
R ⋅R
20 ⋅ 30
RBA = 1 2 =
= 12 Ω
R1 + R2 20 + 30
R AC =
R 4 ⋅ R5
10 ⋅ 10
=
=5 Ω
R 4 + R5 10 + 10
Disegno del circuito:
Si disegna un nuovo circuito in cui vengono sostituite le due resistenze R1, R2 con la sola
resistenza RBA e le due resistenze R4, R5 con la sola resistenza RAC.
B
A
RBA
R3
RAC
+
E
C
figura n. 2
Ricerca di resistenze in serie:
Le resistenze RAC , RBA ed R3 risultano in serie perché sono disposte sullo stesso ramo.
Calcolo della resistenza equivalente;
RT = R AC + RBA + R3 = 12 + 5 + 13 = 30 Ω
Disegno del circuito:
Si disegna un nuovo circuito in cui vengono sostituite le tre resistenze RAC , RBA ed R3 con
la sola resistenza RT.
+
RT
E
figura n. 3
2
Circuiti con un solo generatore di tensione – esercizio n. 3
riduzione del circuito ad una sola resistenza
Calcolo della corrente totale:
Si determina il verso della corrente nel circuito di figura n. 3 utilizzando la convenzione
dell’utilizzatore e se ne calcola il valore.
(La corrente nell’utilizzatore è considerata positiva se scorre dal potenziale maggiore a
quello minore).
IT
+
RT
E
figura n. 3
IT =
E 90
=
=3 A
RT 30
Calcolo delle differenze di potenziale VAC e VBA:
Si determina la d.d.p. VBA fra i punti B e A in figura n. 2
Si determina la d.d.p. VAC fra i punti A e C in figura n. 2
B
A
RBA
R3
RAC
IT
+
E
C
figura n. 2
VBA = RBA ⋅ IT = 12 ⋅ 3 = 36 V
VAC = R AC ⋅ IT = 5 ⋅ 3 = 15 V
Calcolo delle correnti I1, I2, I4, ed I5 in figura n. 1
Conoscendo il valore della d.d.p. VBA è possibile calcolare le correnti I1 ed I2 nelle
resistenze comprese tra i nodi B e A in figura n. 1.
Conoscendo il valore della d.d.p. VAC è possibile calcolare le correnti I4 ed I5 nelle
resistenze comprese tra i nodi A e C in figura n. 1.
3
Circuiti con un solo generatore di tensione – esercizio n. 3
riduzione del circuito ad una sola resistenza
R1
R2
B
A
A
I2
I1
R3
IT
R4
I4
R5
I5
+
E
C
figura n. 1
I1 =
VBA 36
=
= 1.8 A
R1 20
I2 =
VBA 36
=
= 1.2 A
R2 30
I4 =
VAC 15
=
= 1.5 A
R 4 10
I5 =
VAC 15
=
= 1.5 A
R5 10
Calcolo della potenza erogata dal generatore:
PE = E ⋅ IT = 90 ⋅ 3 = 270 W
Calcolo delle potenze assorbite dalle resistenze;
PR1 = R1 ⋅ I12 = 20 ⋅ 1.82 = 64.8 W
PR2 = R2 ⋅ I2 2 = 30 ⋅ 1.22 = 43.2 W
PR3 = R3 ⋅ IT 2 = 13 ⋅ 32 = 117 W
PR4 = R 4 ⋅ I4 2 = 10 ⋅ 1.52 = 22.5 W
PR5 = R5 ⋅ I5 2 = 10 ⋅ 1.52 = 22.5 W
NB: Si noti come la potenza erogata dal generatore è pari alla somma delle potenze
dissipate su ciascuna resistenza presente nel circuito.
4