Alcuni risultati dovuti a Girolamo Saccheri
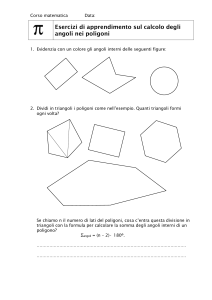
1. Definizione. Consideriamo un quadrilatero Q. Se gli angoli in A e in B sono entrambi
retti e se i lati AD e BC sono congruenti, Q si dice quadrilatero birettangolo isoscele (o di
Saccheri) sulla base AB. Se invece sono retti gli angoli in A, B, C, allora Q si dice
quadrilatero trirettangolo (o di Lambert).
D
C
=
D
C
A
B
=
A
B
2. Esercizio/osservazione. Provare a dimostrare che entrambi i quadrilateri precedenti
sono dei rettangoli, osservando che le dimostrazioni dipendono comunque dal V postulato (o
da una sua formulazione equivalente).
Proveremo a dedurre delle proprietà di questi quadrilateri nella geometria assoluta: nella
geometria che assume tutti i postulati espliciti ed impliciti delle geometria euclidea (ed
elencati in modo completo da Hilbert) con l’eccezione del V postulato.
3. Proposizione. Sia ABCD un quadrilatero con gli angoli in A e in B sono entrambi retti. I
lati AD e BC sono congruenti (ossia ABCD è un quadrilatero birettangolo isoscele) se e solo
se gli angoli interni in C e in D sono congruenti. Se i lati AD e BD sono disuguali, anche gli
angoli in D e in C lo sono ed è maggiore l’angolo adiacente a lato minore e viceversa.
Dim. Consideriamo un quadrilatero di Saccheri ABCD e siano M, N i punti medi dei lati AB e
CD rispettivamente. Consideriamo poi i triangoli ADM e BCM: sono congruenti (per LAL), di
conseguenza DM e CM sono congruenti come anche gli angoli AMD BMC, allora sono
congruenti (per LLL) i triangoli DMN e CMN sono congruenti ed in particolare lo sono gli
angoli MDN e MCN. Si noti, di passaggio, che allora il segmento MN è asse di entrambi i lati
AB e CD.
N
D
C
_
A
B
M
Allora gli angoli interni al quadrilatero in C e in D sono congruenti in quanto somme di
angoli congruenti.
Se invece i lati AD e BC sono disuguali (supponiamo AD > BC), prolunghiamo il lato BC dalla
parte di C fino ad un punto E tale che BE sia congruente ad AD.
D
E
C
C
_
A
B
1
Allora il quadrilatero di ABED è di Saccheri sulla base AB quindi , per quanto appena
dimostrato, gli angoli ADE e BED sono congruenti. Ma l’angolo BCD risulta così angolo
esterno del triangolo DEC e pertanto per il teorema debole dell’angolo esterno BCD > BED.
Si conclude osservando che l’angolo ADC è minore dell’angolo ADE in quando incluso in esso
e quindi è maggiore l’angolo adiacente a lato minore.
Un argomento simile permette di dimostrare il viceversa della prima parte dell’enunciato:
infatti se ora gli angoli interni in C e in D sono congruenti ma non lo fossero i lati AD e BC
allora, supponendo per fissare le idee AD > BC si potrebbe prolungare BC fino ad E come
prima ottenendo di nuovo un quadrilatero di Saccheri ABED, allora per la prima parte della
dimostrazione, per il teorema debole dell’angolo esterno e per inclusione di angoli si
avrebbe tra i corrispettivi angoli: ADC < ADE DEB < DCB mentre, per ipotesi, gli angoli
ADC e DCB sono congruenti.
Si conclude osservando che se se sono gli angoli ad essere disuguali allora per la prima
parte della proposizione anche i lati devono essere disuguali con la relazione fra gli angoli
opposta a quella fra i lati adiacenti.
4. Osservazione/notazioni. In un quadrilatero di Saccheri ABCD di base AB, gli angoli in
C ed in D sono congruenti. Allora si verifica uno dei seguenti casi:
IR: ∢C = ∢D = un angolo retto (ipotesi dell’angolo retto)
IO: ∢C = ∢D > un angolo ottuso (ipotesi dell’angolo ottuso)
IA: ∢C = ∢D < un angolo acuto (ipotesi dell’angolo acuto)
Saccheri dimostra (noi non lo faremo) che se vale una delle tre ipotesi in un particolare
quadrilatero birettangolo isoscele, allora la stessa ipotesi vale in ogni altro quadrilatero
birettangolo isoscele.
Solo IR comporta che la somma degli angoli interni di ABCD sia 4 angoli retti, quindi è
l’unica coerente con il quinto postulato euclideo. Il lavoro di Saccheri è teso a dimostrare
che sia IO sia IA conducono ad una contraddizione: l’obbiettivo è raggiunto solo per IO.
5. Osservazione. Consideriamo un quadrilatero di Saccheri ABCD sulla base AB. Nel corso
della dimostrazione della proposizione 3 si è provato che il segmento che unisce i punti medi
dei lati AB e CD è ortogonale ad entrambi
N
D
C
_
A
M
B
Quindi entrambi i quadrilateri MNAD e MNCB sono trirettangoli pertanto le analoghe ipotesi
sugli angoli possono essere fatte su di essi. Si noti in particolare che, sempre per la
proposizione 3, IR comporta che NC sia congruente MB quindi che CD sia congruente ad AB,
mentre IO comporta NC < MB, quindi CD < AB ed IA comporta NC > MB, quindi CD > AB.
Quindi, dato un quadrilatero di Saccheri ABCD con base AB, si ha:
2
IR ⇔ DC AB
IO ⇔ DC < AB
IA ⇔ DC > AB
Viceversa dato un quadrilatero trirettangolo ABCD con angoli retti in A, B, C, prolungando i
lati DA e CB fino ai punti EF in modo che CB BE e DA AF si ottiene il quadrilatero ECDF
che è un quadrilatero di Saccheri sulla base EC. Infatti i triangoli ADB e AFB sono congruenti
per LAL, in particolare BD BF e ∢DBA ∢FBA da cui ∢CBD ∢EBF ed allora sono
congruenti i triangoli BCD e BEF per LAL.
D
_
A
C
=
B
_
F
=
E
Ne segue che se vale una delle tre ipotesi sul quarto angolo in un particolare quadrilatero
trirettangolo, allora la stessa ipotesi vale in ogni altro quadrilatero trirettangolo e che vale
una delle tre ipotesi per i quadrilateri di saccheri se e solo se la stessa ipotesi vale per i
quadrilateri di Lambert.
Ai fini della verifica dell’ipotesi euclidea lavorare con i quadrilateri di Saccheri equivale a
lavorare con i quadrilateri trirettangoli.
6. Proposizione. Vale l’ipotesi IR, oppure IO, oppure IA se e solo se che la somma degli
angoli interni di un triangolo è rispettivamente uguale, oppure maggiore, oppure minore di
due angoli retti.
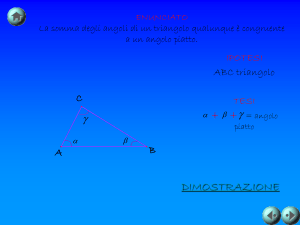
Dim. Dato che ogni triangolo è diviso in due triangoli rettangoli da una delle altezze, basta
dimostrare il risultato per triangoli rettangoli.
Sia ora ABC un triangolo rettangolo in B e completiamolo ad un quadrilatero tracciando il
segmento AD congruente a BC e ad perpendicolare ad AB: è un quadrilatero di Saccheri
sulla base AB.
D
_
A
C
_
B
Se vale IR, i triangoli ABC e ADC sono congruenti (perché?) e la somma degli angoli interni
al triangolo ABC è due retti.
3
Nel caso IO AB è maggiore di CD, quindi l’angolo ACB è maggiore dell’angolo CAD: si tratta
di angoli compresi fra copie di lati ordinatamente congruenti in due triangoli i cui lati opposti
sono invece disuguali: allora a lato maggiore si oppone angolo maggiore.
Allora 2R = ∢DAB + ∢ABC = ∢CAD + ∢CAB + ∢ABC < ∢ACB + ∢CAB + ∢ABC, che è la
somma degli angoli interni di ABC.
Il caso IA procede in modo analogo, ma ora CD è maggiore di AB e l’angolo ACB è minore
dell’angolo CAD e quindi 2R > ∢ACB + ∢CAB + ∢ABC.
7. Lemma. Se in un triangolo rettangolo ABC rettangolo in B, M è il punto medio
dell’ipotenusa AC e H il piede della perpendicolare condotta da M al cateto AB allora AH
risulta congruente, minore, maggiore di HB a seconda che valga rispettivamente IR, IO,
IA.
Dim. Infatti conduciamo da M entrambe le perpendicolari ai cateti MH, MK il quadrilatero
HBKM è trirettangolo e quindi (per l’osservazione 5) l’angolo HMK risulta retto, ottuso
oppure acuto (e scriviamo ∢HMK = R, ∢HMK > R, ∢HMK < R) a seconda che valga IR, IO
oppure IA e nelle stesse ipotesi MK risulta congruente, minore o maggiore di HB.
C
M
A
K
H
B
Confrontiamo ora fra loro i triangoli rettangoli AHM e MKC con ipotenuse congruenti. Basta
dimostrare che AH risulta congruente, minore o maggiore di MK a seconda di IR, IO, IA e
questo segue dal fatto che l’angolo AMH sia congruente, minore o maggiore dell’angolo MCK
nelle tre ipotesi considerate.
Nell’ipotesi IR gli angoli considerati sono congruenti (è la condizione necessaria al
parallelismo delle rette supporto di HM e BC entrambe perpendicolari alla stessa retta
supporto di AB). In altro modo possiamo osservare che la somma degli angoli interni del
triangolo MCK (come di ogni triangolo) vale due angoli retti (e scriviamo S(MCK) = 2R).
Tuttavia, indipendentemente dall’ipotesi angolare considerata, è di due angoli retti la
somma degli angoli AMH, HMK, KMC. Allora in IR risulta ∢AMH + ∢HMK + ∢KMC = 2R =
S(MCK) = ∢KMC + ∢MCK + ∢CKM, da cui ∢AMH + ∢HMK = ∢MCK + ∢CKM. Ora ∢CKM =
R (indipendentemente dall’ipotesi angolare) mentre in IR anche ∢CKM = R. Da cui ∢AMH =
∢MCK. Questa seconda dimostrazione si adatta anche alle altre ipotesi angolari.
Infatti in IO si ha: ∢AMH + ∢HMK + ∢KMC =2R < S(MCK) = ∢KMC + ∢MCK + ∢CKM:
infatti la somma degli angoli interni di un triangolo questa volta è maggiore di due angoli
retti. Quindi ∢AMH + ∢HMK < ∢MCK + ∢CKM ed ora ∢CKM = R < ∢HMK, quindi ∢AMH <
∢MCK. Nel caso IA si ha: ∢AMH + ∢HMK + ∢KMC > ∢KMC + ∢MCK + ∢CKM, da cui ∢AMH
+ ∢HMK > ∢MCK + ∢CKM e quindi ∢AMH > ∢MCK, dato che ∢CKM = R > ∢HMK.
8. Corollario. Date due rette incidenti oblique e considerando su una di esse dei segmenti
consecutivi fra loro congruenti, le loro proiezioni sull’altra retta risultano essere fra loro
congruenti, crescenti o decrescenti a seconda di IR, IO, IA.
Dim. Segue dal lemma 7 (fare nei dettagli).
9. Osservazione. Grazie a questi risultati Saccheri dimostra che IR ed IO implicano il
postulato dell’obliqua, equivalente al quinto postulato euclideo, mentre solo IR è coerente
4
con esso. Nel caso quindi di IO perviene correttamente ad una contraddizione usando la
consequentia mirabilis, ossia la tautologia (¬P
P)
P, ed enuncia quella che nel suo
trattato è la proposizione XIV:
Hypothesis anguli obtusi est absolute falsa, quia se ipsam destruit
(l’ipotesi dell’angolo ottuso è completamente falsa perché distrugge se stessa) e che segue
quindi dal
10. Teorema. In IR ed in IO una perpendicolare ed un obliqua ad una retta data si
incontrano.
Dim. Siano AC e BD rispettivamente un’obliqua ed una perpendicolare alla stessa retta t con
A e B punti distinti di t come illustrato nel disegno
C
D
A
B
t
Prendiamo un punto A1 su AC e sia H1 la sua proiezione ortogonale su t. Prendiamo poi su
AC i segmenti consecutivi A1A2, A2A3, A3A 4 … tutti congruenti ad AA1. I corrispondenti
segmenti AH1, H1H2, H2H3 … sono tutti congruenti in IR e crescenti in IO per il corollario 8.
In entrambi i casi (in una assiomatizzazione esplicita come quella hilbertiana per l’assioma
di Archimede) esiste un intero n tale che AH include il segmento AB.
C
An
A1
A
A2
H1
A3
H2 H3
D
B
Hn
t
Abbiamo così un triangolo AHnAn con una retta BD che entra nel triangolo passando per un
punto interno del lato AHn.
Nelle assiomatizzazioni esplicite viene postulato (o dimostrato a partire da uno dei sui
equivalenti) un assioma che viene detto assioma di Pasch, indipendente dal V postulato ed
implicito nel trattato euclideo: se retta che attraversa un lato di un triangolo che non sia un
estremo, deve necessariamente attraversare un altro dei due lati o il vertice in comune tra
esse.
La retta BD deve quindi intersecare uno degli altri lati del triangolo, ma non può intersecarlo
nel lato HnAn: infatti la rette BD e HnAn sono perpendicolari alla medesima retta t e quindi,
se si intersecassero, avremmo un triangolo con due angoli retti, contro il teorema debole
dell’angolo esterno. In definitiva la retta sostegno di BD deve intersecare il lato AA n in un
punto interno e quindi la retta supporto di esso.
5
11. Osservazioni. La dimostrazione di Saccheri della contraddittorietà dell’ipotesi
dell’angolo ottuso nella geometria assoluta (ossia nella geometria che ammette tutti i
postulati espliciti ed impliciti della geometria euclidea con l’eccezione del quinto) consente di
poter enunciare il seguente risultato attribuibile, appunto, fra i molti anche a Saccheri:
Nella geometria assoluta la somma degli angoli interni di un triangolo non è superiore a due
angoli retti.
L’argomento sviluppato nel teorema 10 funziona correttamente in IR, IO, ma non in IA.
Infatti per il corollario 8 i segmenti sulla retta t sono tutti congruenti o sono crescenti in IR
e in IO e questo è sufficiente per superare da un certo indice in poi il punto B, ma nel caso
IA, essendo decrescenti, non possiamo dedurlo. Correttamente Saccheri usa il corollario in
questione solo per IR ed IO. Per IA svolge considerazioni diverse dimostrando innanzitutto
una serie di risultati che, contro le sue aspettative, sono veri e propri teoremi validi in una
diversa geometria detta iperbolica. Egli ne deduce un comportamento asintotico per le rette
parallele che, se così si può dire, può essere descritto come l’esistenza all’infinito di una
perpendicolare comune alle due rette parallele e passante per il punto all’infinito al quale
asintoticamente tendono entrambe le rette. Dato che due rette che passano per uno stesso
punto (al finito) e sono perpendicolari ad una stessa retta per quel punto coincidono,
Saccheri ne trae quella che nel suo trattato è la proposizione 33:
Hypothesis anguli acuti est absolute falsa; quia repugnans naturae lineae rectae.
(l’ipotesi dell’angolo acuto è assolutamente falsa perché ripugna alla natura della linea
retta)
La diversa formulazione di questa proposizione rispetto alla XIV del suo trattato può far
supporre che Saccheri stesso, rendendosi conto del diverso statuto epistemologico delle due
argomentazioni, non fosse perplesso di fronte a quest’ultima. A conforto di ciò c’è il fatto
che egli nelle successive proposizioni cerca di contraddire l’ipotesi dell’angolo acuto in altro
modo: in base al concetto di equidistanza e con argomenti vicini al calcolo infinitesimale, ma
commette degli errori: tuttavia è bene ricordare che il calcolo era stato introdotto e
cominciava ad essere sviluppato solo da pochi decenni. Saccheri riassume queste ulteriori
argomentazioni nella proposizione XXXVIII del suo trattato e nuovamente nella stessa
forma della XIV:
Hypothesis anguli acuti est absolute falsa, quia se ipsam destruit
6