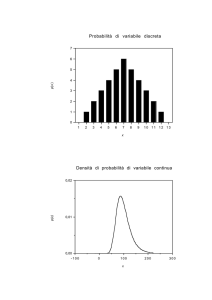
DISTRIBUZIONE di PROBABILITA’
Si dice variabile aleatoria (o casuale) discreta X una quantità variabile che può assumere i
valori: x1; x2;……, xn
al verificarsi degli eventi incompatibili e complementari: E1; E2;…..; En
le cui probabilità sono: p1; p2;……..; pn
tali che Σpi = 1
eventi incompatibili: il verificarsi di uno di essi esclude il verificarsi contemporaneo di qualsiasi
altro evento
complementari: uno di essi deve necessariamente verificarsi
VALORE MEDIO DI UNA VARIABILE CASUALE
M (X ) =
p1 x1 + p 2 x 2 + ⋅ ⋅ ⋅ ⋅ + p n x n
= p1 x1 + p 2 x 2 + ⋅ ⋅ ⋅ ⋅ + p n x n
∑ pi
Il valore medio (o speranza matematica*, o valore atteso, o valore sperato) di una variabile
casuale è dato dalla somma dei prodotti dei valori che la variabile può assumere per le rispettive
probabilità e quindi è la media ponderata dei possibili valori di x.
Ex. Calcolare il valore medio ottenibile nel lancio di un dado.
x1 = 1; x2 = 2; x3 = 3; x4 = 4; x5 = 5; x6 = 6
1
1
1
1
1 7
1
M ( X ) = 1 + 2 + 3 + 4 + 5 + 6 = = 3,5
6
6
6
6
6 2
6
* Il termine speranza matematica è storicamente legato ai giochi d’azzardo.
Un gioco si dice equo se la speranza matematica di ogni giocatore è nulla.
Ex. Giocando alla roulette, puntiamo una certa somma S su un numero e sappiamo che, se il numero
esce ritiriamo 35 volte la somma che abbiamo impegnato, se il numero non esce perdiamo quello
che abbiamo puntato. Qual è il valore atteso di questo gioco?
1/12
I numeri della roulette sono 37, quindi ognuno di essi ha probabilità 1/37 di uscire e 36/37 di non
uscire. Se il numero esce vinciamo una somma pari a 35S e se non esce perdiamo S. Il valore atteso
del guadagno che abbiamo giocando alla roulette è M ( X ) = 35S
1
36
1
−S
=− S.
37
37
37
Si ha dunque un guadagno medio negativo; non appare allora conveniente giocare alla roulette
puntando su un numero pieno.
SCARTO LINEARE DI UNA VARIABILE CASUALE
Detto M(X) = m si definisce scarto (o scostamento o deviazione) la nuova variabile
Y = X - m tale che M(Y) = M(X-m)= M(X) –M(m)= m - m = 0.
Ex: Calcolare lo scarto riferito all’esercizio precedente e verificare la media dello scarto.
y1 = 1 −
7
5
=− ;
2
2
y6 = 6 −
7 5
5 3 1 1 3 5
= ; M (Y ) = − − − + + + = 0
2 2
3 2 2 2 2 2
y2 = 2 −
7
3
=− ;
2
2
y3 = 3 −
7
1
=− ;
2
2
y4 = 4 −
7 1
= ;
2 2
y5 = 5 −
7 3
= ;
2 2
VARIANZA: SCARTO AL QUADRATO
Per evitare che gli scarti negativi annullino gli scarti positivi si considerano i quadrati degli
scarti.
Si dice variabile casuale scarto al quadrato
( X − m )2
la variabile casuale che assume i valori
(x1 − m )2 ; (x 2 − m )2 , …….., (x n − m )2
Si dice varianza della variabile casuale X il valore medio dello scarto quadrato ( X − m )
( )
2
var( X ) = M ( X − m ) = M X 2 − [M ( X )]
2
2
La varianza è uguale alla differenza fra il valore medio della variabile casuale quadrato e il quadrato
del valore medio.
2/12
SCARTO QUADRATICO MEDIO DI UNA VARIABILE CASUALE
Lo scarto quadratico medio (o scostamento, o deviazione quadratica media) è dato dalla
radice quadrata del valore medio dei quadrati degli scarti lineari.
[
σ = M ( X − m )2
]
la conoscenza di σ è molto utile per prevedere l’ampiezza dei valori dello scarto X-m
Ex. Calcolare la media aritmetica, lo scarto lineare, lo scarto quadratico medio e la varianza con i
seguenti dati:
3, 7, 12 e 20 con probabilità 0,30; 0,25; 0,31 e 0,14
xk
pk
xk pk
xk-M
(xk-M)2
pk(xk-M)
pk(xk-M)2
3
0,30
0,90
-6,17
38,07
-1,85
11,42
7
0,25
1,75
-2,17
4,71
-0,54
1,18
12
0,31
3,72
2,83
8,01
0,88
2,48
20
0,14
2,80
10,83
117,29
1,51
16,42
Totali
1,00
9,17
0,00
31,50
M (X ) =
σ
5,61
Σxi pi 9,17
=
= 9,17
Σp x
1
M ( X − m ) = Σp i ( xi − M ) = 0
( )
var( X ) = M ( X − m ) = M X 2 − [M ( X )] = 31,50
2
[
]
σ = M ( X − m )2 = 5,61
VALORE MEDIO NELLE PROVE RIPETUTE
Se un evento E ha la probabilità costante p di verificarsi in ogni prova, e di conseguenza
l’evento contrario ha probabilità q = 1 – p, effettuando n prove nelle medesime condizioni, il
3/12
numero delle volte l’evento E si verifica costituisce una variabile casuale X, che può assumere
differenti valori ciascuno con una prevista probabilità.
M ( X ) = np
Quindi se un evento, su n prove effettuate nelle medesime condizioni, ha la probabilità costante p in
ogni prova, il valor medio del numero delle volte che l’evento richiesto si verifica è dato dal
prodotto del numero delle prove effettuate per la probabilità costante dell’evento in ogni prova.
Ex. Viene ripetuto il lancio del dado per 600 volte, il numero delle volte che si presenterà il vale 3 è
dado da M (3) = 600 ⋅
1
= 100 quindi su 600 prove effettuate il valore 3 in media si presenterà 100
6
volte.
SCARTO NELLE PROVE RIPETUTE
Se si ripetono n prove, ciascuna di probabilità costante p in ogni prova e l’evento si presenta
ν (frequenza) volte, si definisce scarto assoluto la differenza fra il numero ν delle volte che l’evento
si è presentato favorevole ed il numero medio M ( X ) = np delle volte che l’evento avrebbe
teoricamente presentarsi. Indicando con s lo scarto assoluto si ha: s = ν - np
Ricordiamo che il valore medio dello scarto assoluto è nullo cioè M(s) = 0.
Il rapporto fra lo scarto assoluto ed il numero delle prove effettuate si definisce scarto
relativo ed è dato da:
s ν − np ν
=
= − p = f − p ossia lo scarto relativo è dato dalla differenza fra
n
n
n
la frequenza relativa con cui l’evento si è presentato e la probabilità costante dell’evento in ciascuna
prova.
Al crescere del numero n delle prove, f si avvicina ad un valore circa uguale a quello della
s
probabilità a priori p del verificarsi dell’avvenimento. M = M ( f − p ) = 0
n
4/12
SCARTO QUADRATICO MEDIO NELLE PROVE RIPETUTE: σ = npq = np(1 − p )
VARIANZA NELLE PROVE RIPETUTE: var( X ) = npq
Continuando l’esercizio precedente: Viene ripetuto il lancio del dado per 600 volte, il numero delle
volte che si presenterà il vale 3 è dado da M (3) = 600 ⋅
valore
3
in
media
1
6
si
presenterà
100
volte,
1
= 100 quindi su 600 prove effettuate il
6
lo
scarto
quadratico
medio
sarà
1
6
σ = np(1 − p ) = 600 1 − ≅ 9,13
VARIABILI CASUALI CONTINUE
Variabile casuale continua è qualsiasi variabile casuale che assume tutti i valori reali
compresi in un dato intervallo limitato o illimitato.
Diamo alcune definizioni:
Funzione di ripartizione: la funzione di ripartizione F(x) della variabile casuale X esprime la
probabilità che la variabile casuale assuma un valore non superiore a x. Cioè, si ha
F ( x) = Pr( X ≤ x) e valgono le medesime proprietà viste per le variabili casuali discrete, cioè:
•
La funzione di ripartizione è definita per qualsiasi valore (reale) di x
•
La funzione di ripartizione assume valori compresi fra zero e 1 essendo:
F ( x) = 0 per x ≤ a (valore minimo)
F ( x) = 1 per x ≥ b (valore massimo)
5/12
•
La funzione di ripartizione è monotona non decrescente.
F(x)
1
0
a
b
Ex. Consideriamo la variabile casuale X, continua, che assume tutti i valori reali appartenenti
all’intervallo [0; 10] e la cui funzione di densità è f(x) = 0,003 x2.
Con riferimento a questa variabile casuale calcoliamo la probabilità che essa assuma valore:
1. non superiore a 1
2. superiore a 1
3. non superiore a 2
4. compreso fra 4 e 7
verifichiamo per prima cosa la condizione che la somma delle probabilità parziale è uguale alla
10
certezza:
3
10
∫ f ( x)dx = ∫ 0,003x
0
2
dx = 0,003
0
x
3
10
= 0,001 ⋅ 10 3 = 1
0
1
Pr ( X ≤ 1) = ∫ 0,003 ⋅ x 2 dx = 0,001
0
10
Pr ( X > 1) = ∫ 0,003 ⋅ x 2 dx = 0,999
1
2
Pr ( X ≤ 2 ) = ∫ 0,003 ⋅ x 2 dx = 0,008
0
6/12
7
Pr (4 < X ≤ 7 ) = ∫ 0,003 ⋅ x 2 dx = 0,0279
4
PARTICOLARI DISTRIBUZIONI DI PROBABILITA’
La distribuzione uniforme
Si dice che la variabile aleatoria X ha distribuzione di probabilità uniforme se assume i
valori 1, 2, 3, ……., n con probabilità p1, p2,……., pn tutte uguali fra loro.
La distribuzione binomiale
Si dice prova di Bernuilli un esperimento aleatorio che può avere solo due esiti possibili,
convenzionalmente chiamati successo e insuccesso aventi probabilità p di successo e q=1-p di
insuccesso.
Si dice processo di Bernouilli una sequenza di prove di Bernouilli tutte di uguale parametro
p e tra loro indipendenti.
La probabilità p k = P ( X = k ) che in un processo bernouilliano si verifichino k successi è
10
data da p k = ⋅ p k ⋅ q n −k con k = 0, 1, 2, …….., n
x
Ex. Una moneta viene lanciata 10 volte e viene registrato il numero delle volte che esce testa. Tale
numero è una variabile aleatoria discreta che può assumere tutti i valori compresi tra 0 e 10; infatti
su 10 lanci, l’evento testa può verificarsi 0 volte, 1 volta,……., 10 volte.
La distribuzione di probabilità di questa variabile aleatoria si determina calcolando la probabilità
che su 10 lanci esca testa 0 volte, 1 volta,……., 10 volte; se indichiamo con px la probabilità che
x
10 1 1
esca x volte si ha p x = ⋅
x 2 2
10 − x
10
10!
con =
x x!(10 − x )!
x
0
1
2
3
4
5
6
7
8
9
10
p
0,001
0,010
0,044
0,117
0,205
0,246
0,205
0,117
0,044
0,010
0,001
7/12
con
∑p
x
=1
grafico
La funzione distribuzione di probabilità della variabile aleatoria X può quindi essere descritta in
forma analitica nel seguente modo:
n
f ( x ) = p( X = x ) = x
⋅ p x ⋅ q n − x ..... per.x = 0,1,......, n
0.....altrove
ex. La probabilità che su 10 estrazioni di una carta da un mazzo di 40 esca per tre volte un asso è:
3
7
10 4 36
p3 = ⋅ ≅ 0,057
3 40 40
Ex. La probabilità che un tiratore non colpisca il bersaglio è 0,08. Calcolare la probabilità che, su 10
tiri, ne fallisca 0, 1, 2, ….., 10.
La variabile aleatoria X è, in questo caso, il numero di tiri non andati a segno sui 10 fatti.
p = 0,08; q = 0,92
10
0
10
p (0 ) = ⋅ (0,08) (0,92 ) = 0,43
0
10
1
9
p (1) = ⋅ (0,08) (0,92 ) = 0,38
1
............................................................
10
5
5
p (5) = ⋅ (0,08) (0,92 ) = 0,0005
5
.............................................................
10
10
0
p (10 ) = ⋅ (0,08) (0,92 ) = 1,07 ⋅ 10−11
10
Il valore atteso è M(X) = 10 0,08 = 0,8
8/12
La varianza è V(X) = 10 0,08 0,92 = 0,736
questo significa che mediamente ci si aspetta che il tiratore sbagli al massimo un tiro su 10 fatti, con
uno scarto da questo valore piuttosto basso.
LA DISTRIBUZIONE DI POISSON
Vedendo gli esempi precedenti se n è grande, la valutazione della probabilità binomiale richiede
calcoli di una certa entità. In questi casi se p è molto piccolo e se n tende ad infinito si può ricorrere
ad un’altra distribuzione che prende il nome di distribuzione di Poisson.
In tale distribuzione, la variabile X assume i valori 0, 1, 2, ….
m x −m
e .... per.x = 0,1,2,...
La funzione distribuzione di probabilità di X assume la forma f ( x ) = x!
0.....altrove
Dove m è una costante positiva che rappresenta il parametro della distribuzione.
Nel caso in cui questa distribuzione venga usata come approssimazione di quella binomiale, quindi
per n molto grande e p molto piccolo, il parametro m è dato dal valore atteso cioè dal prodotto np.
Oltre che come approssimazione della distribuzione binomiale per n grande e p piccolo, la
distribuzione di Poisson regola molti fenomeni naturali a patto che questi rispettino le seguenti
condizioni:
•
la probabilità che un evento si verifichi in un fissato intervallo di tempo cresca con
l’ampiezza dell’intervallo.
•
La probabilità che un evento si verifichi due volte nello stesso intervallo sia trascurabile
rispetto alla probabilità che si verifichi una sola volta.
•
Il numero di eventi in intervalli disgiunti siano indipendenti.
Ex. Vogliamo calcolare la probabilità che, lanciando due dadi insieme per 36 volte, l’evento “esce
un doppio 2” si verifichi 0, 1, 2, …….36 volte.
9/12
Sia X la variabile aleatoria che registra il numero di doppia uscita del 2. La probabilità che in un
lancio dei due dadi si verifichi un doppio due è 1/36, la probabilità che non si verifichi è 35/36 ed
inoltre n = 36.
Se calcoliamo i valori di probabilità con la discussione binomiale (funzione di probabilità
x
36 1 35
f ( x ) = ⋅ ⋅
x 36 36
ottiene per m = np = 36
36 − x
) e con la distribuzione di Poisson (funzione di probabilità che si
1
1!
= 1 , cioè f ( x ) = e −1 ) otteniamo
36
x!
x
Distrib. binomiale
Distrib. Di Poisson
0
0,363
0,368
1
0,273
0,368
2
0,187
0,184
3
0,060
0,061
4
0,014
0,015
5
0,003
0,003
6
0,000
0,001
Come si può vedere la differenza fra la probabilità calcolata con la distribuzione binomiale e quella
di Poisson diventa trascurabile al crescere dei valori assunti da X.
Ex. In un ufficio postale transitano, per un certo sportello mediamente 90 persone ogni ora. Se
l’operatore si deve allontanare 5 minuti, qual è la probabilità che non arrivino persone in quei 5
minuti?
Qual è la probabilità che arrivino 3 persone?
Se allo sportello si presentano 90 persone ogni ora, in 5 minuti si presentano mediamente x = 7,5
persone.
10/12
Il numero di persone che si presentano effettivamente in quei 5 minuti è una variabile aleatoria
discreta che può assumere i valori 0, 1, 2, …. Tale variabile segue una distribuzione di Poisson in
cui il parametro m vale 7,5; quindi la probabilità che non si presentino persone allo sportello è
f (0 ) = p ( X = 0) =
(7,5)0 e −7,5 = 5,5 ⋅ 10 −4
f (3) = p ( X = 3) =
(7,5)3 e −7,5 = 0,04
0!
(probabilità molto bassa)
3!
VARIABILE CASUALE CON DISTRIBUZIONE GAUSSIANA
Si tratta della variabile casuale continua che assume qualsiasi valore reale (da − ∞ a + ∞ ) e
la cui funzione di densità, che indichiamo con il simbolo p (x) , è definita come segue:
p (x ) =
1
σ ⋅ 2π
−
e
( x − m )2
2σ 2
Dove m è il valore medio; σ 2 è la varianza e σ è lo scarto quadratico medio.
Essa dipende dai due valori m e σ 2 .
Dallo studio della funzione di densità p( x ) della variabile casuale gaussiana si deduce che essa ha
le seguenti caratteristiche:
•
è simmetrica rispetto alla retta x=m
•
assume il massimo valore uguale a
•
presenta due punti di flesso in corrispondenza di m − σ ed m + σ ;
•
è asintotica rispetto all’asse delle ascisse;
•
l’area sottesa dalla curva e delimitata dall’asse x ha valore 1;
•
il valore atteso e la deviazione standard sono proprio i parametri m e σ
1
in corrispondenza della media m ;
σ 2π
11/12
p(x)
0
andamento della funzione di densità p(x)
m-σ
m
m+σ
x
La sua tipica forma a campana è più o meno concentrata rispetto all’asse x = m, cioè per σ piccoli cresce il valore
massimo e quindi la curva è più alta e più addensata all’asse x = m mentre per alti valori di σ la curva è più bassa e
distribuita.
La probabilità che la variabile aleatoria assuma un valore x che è compreso tra due particolari valori a e b è data
dall’area della regione di piano racchiusa dalla curva, dall’asse delle ascisse e dalle rette x=a e x=b.
Esempio: consideriamo la variabile aleatoria che rappresenta il diametro delle sfere di acciaio prodotte da una macchina
utensile e supponiamo di sapere che le caratteristiche della macchina facciano ottenere sfere con un diametro di valor
medio 0,5 cm e deviazione standard 0,02 cm; la curva teorica di probabilità ha in questo caso equazione
( x − 0,5 )2
−
2
1
f ( x) =
e 2(0, 02 ) per valutare la probabilità che una sfera presa a caso dalla distribuzione abbia diametro
0,02 2π
compreso fra 0,475 cm 0,525cm, dobbiamo calcolare l’area della parte di piano racchiusa dalla curva, dall’asse delle
ascisse e dalle rette di equazioni x=0,475 e x=0,525.
Variabile casuale gaussiana standardizzata: con m = 0 e σ2 = 1 la formula della distribuzione diventa
p( x ) =
x2
x2
−
1 −2
e ≅ 0,39894 ⋅ e 2
2π
Questa funzione
•
assume il valore massimo in corrispondenza di x = m = 0 e vale
•
presenta i due punti di flesso in corrispondenza di -1 e +1
1
;
2π
p(x)
0
x
12/12