Superfici di Riferimento (1/4)
La definizione di una superficie di riferimento nasce dalla necessità di avere un supporto matematico su cui sviluppare il
rilievo eseguito sulla superficie terrestre. Tale superficie deve:
• rappresentare nel miglior modo possibile la reale forma della superficie terrestre;
• essere esprimibile attraverso una formulazione matematica semplice.
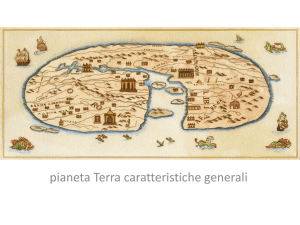
Qualunque punto P di massa m posto sulla superficie terrestre è sottoposto a
delle forze
Forza Centrifuga
Forza di Attrazione
Gravitazionale
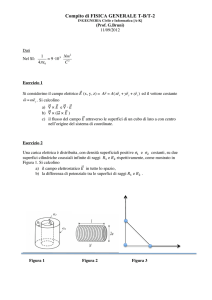
f ma m 2 r
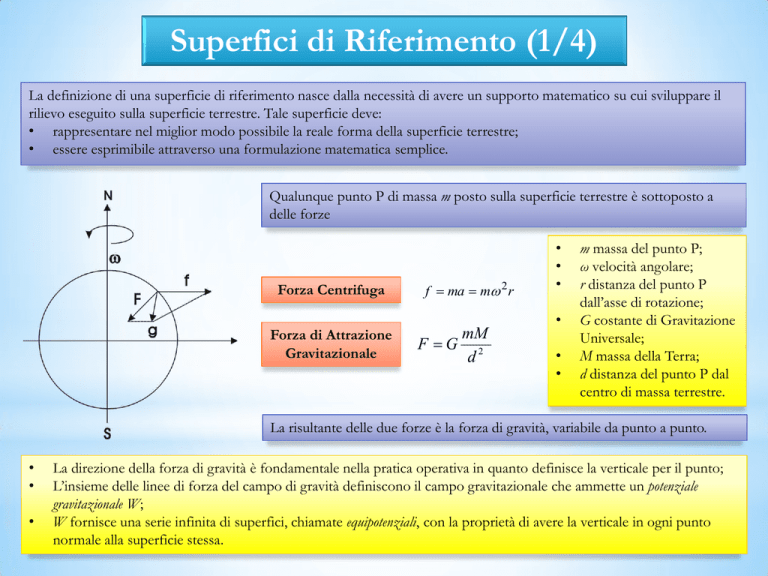
mM
F G 2
d
•
•
•
•
•
•
m massa del punto P;
ω velocità angolare;
r distanza del punto P
dall’asse di rotazione;
G costante di Gravitazione
Universale;
M massa della Terra;
d distanza del punto P dal
centro di massa terrestre.
La risultante delle due forze è la forza di gravità, variabile da punto a punto.
•
•
•
La direzione della forza di gravità è fondamentale nella pratica operativa in quanto definisce la verticale per il punto;
L’insieme delle linee di forza del campo di gravità definiscono il campo gravitazionale che ammette un potenziale
gravitazionale W;
W fornisce una serie infinita di superfici, chiamate equipotenziali, con la proprietà di avere la verticale in ogni punto
normale alla superficie stessa.
Superfici di Riferimento (2/4)
Geoide
Supponendo la massa terrestre costituita da un liquido in quiete (assenza d
moti e correnti), essa si disporrebbe secondo una delle superfici equipotenziali
(W costante) scelta in modo da essere passante per un determinato punto in un
determinato istante.
dm 2 2
W x, y , z G
x y2 c
r
2
T
Di complessa trattazione analitica perché richiede
la conoscenza della legge di distribuzione della
massa all’interno della Terra
Quota Ortometrica
Sferoide
Lunghezza della linea di forza
compresa tra la superficie
equipotenziale passante per il punto
P e il geoide
Superficie che si otterrebbe supponendo una distribuzione della massa
simmetrica rispetto all’asse di rotazione terrestre.
Risulta complesso definire alcuni sistemi di coordinate su tale superficie
Superfici di Riferimento (3/4)
Ellissoide
Superficie ottenuta dalla rotazione attorno all’asse terrestre di un ellisse di
semiasse maggiore a e semiasse minore b.
Espressione
Analitica
Ellissoide
a
α
Helmert (1906)
6 378 200 m
1/298,3
Hayford (1909)
6 378 388 m
1/297
x2 y2
a2
z2
b2
1
ab
a
Schiacciamento
Prima
Eccentricità
e2
a2 b2
a2
Superfici di Riferimento (4/4)
Coordinate
Ellissoidiche
Consentono di definire la posizione di un punto rispetto alla superficie
dell’ellissoide.
Latitudine
Meridiani
Paralleli
angolo di inclinazione φ formato dalla normale n
passante per un punto P ed il piano equatoriale
Longitudine
angolo diedro λ formato tra un piano di riferimento
passante per l’asse di rotazione ed il piano passante per il
punto P e l’asse di rotazione
Quota
Ellissoidica
distanza fra il punto P e la superficie di riferimento,
misurata lungo la normale n passante per il punto
Insieme dei punti sulla superficie di riferimento caratterizzati da uguale
longitudine. Il meridiano di riferimento (λ = 0) è quello passante per Greenwich.
Insieme dei punti sulla superficie di riferimento caratterizzati da uguale
latitudine. Il parallelo di riferimento (φ = 0) è quello passante per l’equatore.
Ondulazione del Geoide
In un punto generico P della superficie fisica terrestre, la verticale
(ossia la tangente alla linea di forza passante per P) generalmente non
coincide con la normale all’ellissoide passante per P.
Deviazione della
Verticale
L’angolo formato tra verticale e normale
all’ellissoide in un punto P.
Ondulazione del
Geoide
Differenza tra quota ellissoidica e quota
geodetica di un punto P.
Raggi Principali di Curvatura
È possibile definire dei raggi di curvatura che caratterizzano la superficie in un determinato punto P. I due raggi di
curvatura fondamentali sono individuabili tagliando la superficie ellissoidica con le due sezioni normali principali per P.
Primo Raggio di
Curvatura
raggio di curvatura ρ del meridiano passante per un
punto P sulla superficie, individuato secando l’ellissoide
con il piano meridiano passante per P.
Grannormale
Raggio della Sfera
Locale
r N cos
1 e
2
sin 2
3
raggio di curvatura ottenuto secando l’ellissoide con un
piano contenente la normale all’ellissoide e
perpendicolare al piano del meridiano.
N
Raggio del Parallelo
passante per P
a 1 e2
a
1 e 2 sin 2
a cos
1 e 2 sin 2
a 1 e2
R N
1 e 2 sin 2
È la superficie sferica che meglio approssima quella
ellissoidica nell’intorno del punto P
Geodetica
Linea congiungente due punti A e B sulla superficie ellissoidica, che gode della proprietà di avere, in ogni punto, la
normale coincidente con la normale alla superficie.
Rappresenta la minima distanza tra due punti su
una superficie:
• è una retta nel caso di una superficie piana;
• è un arco di cerchio massimo nel caso di
superficie sferica.
Dati due punti A, B sulla superficie ellissoidica, si
considerano:
• il piano ПA contenente la normale per A e il
punto B;
• il piano ПB contenente la normale per B e il
punto A;
Si individuano le sezioni normali come le
intersezioni tra i due piani e l’ellissoide. La
geodetica è una curva compresa tra le due sezioni
normali.
•
•
Tra i paralleli, solo l’equatore è una
geodetica;
Qualunque meridiano è una geodetica.
Sistemi di Coordinate
Geodetiche
Polari
Le coordinate del punto P sono espresse, rispetto ad una origine O,
attraverso la lunghezza s dell’arco di geodetica congiungente P ad
O e l’angolo α tra la geodetica e il meridiano passante per O.
Geodetiche
Ortogonali
Le coordinate del punto P sono espresse, rispetto ad una origine
O, attraverso la lunghezza dell’arco di geodetica Y congiungente P
a P′ (ortogonale al meridiano in P′) e la lunghezza dell’arco di
geodetica X = OP′.
Sono alla base della cartografia catastale italiana, che presenta
diverse emanazioni (origini) sul territorio
Cartesiane
Le coordinate del punto P sono espresse, rispetto ad una origine
O, attraverso la terna ortogonale cartesiana individuata dal sistema
di riferimento scelto.
Utilizzato nell’ambito della geodesia spaziale (GPS ed altre
tecniche) anche per orientare ellissoidi di riferimento validi a livello
globale
Relazione tra Coord. Ellissoidiche e Cartesiane
x r cos N cos cos
y r sin N cos sin
a 1 e 2 sin
z
N 1 e 2 sin
1 e 2 sin 2
Punto sulla
superficie
Sistema facilmente invertibile. Si calcola ω da x e y, poi φ da z e una tra
x e y.
Punto con quota
h
r x 2 y 2 N h cos
z N h sin
Ne 2 sin
Ne 2
tan
1
r N h cos N h cos N h
z 1
1 arctan
2
r 1 e
a
N1
1 e 2 sin 2 1
x N h cos cos
y N h cos sin
z N 1 e 2 h sin
1.
2.
3.
4.
Si determina la distanza r del punto rispetto all’asse Z;
Si calcola il rapporto z/r e si pone h0 = 0 per calcolare
un primo valore φ1, a cui corrisponde un valore N1;
Con N1 e φ1 si determina un nuovo valore h1 dalla r;
N1 e h1 si sostituiscono in z/r per determinare h2 e il
procedimento viene ripetuto iterativamente sin
quando la differenza tra due valori consecutivi di N è
opportunamente piccola.
Soluzioni Approssimate dell’Ellissoide
Nei calcoli topografici è possibile approssimare la reale forma della Terra con le tre superfici: ellissoidica, sferica e piana.
Ciò comporta una semplificazione in termini analitici. Sarà possibile scegliere una delle tre superfici di riferimento in
relazione a:
• estensione areale del rilievo;
• precisione richiesta.
Misura di
Distanze
Precisione massima raggiungibile di 1 mm / 1 km (10–6)
sia in planimetria che in quota
Misura di
Angoli
Precisione massima raggiungibile di 0,1′′ (≈ 0,5∙10–6 rad)
Campo
Geodetico
distanza entro la quale la differenza relativa tra le
coordinate di un punto sulla sfera locale tangente
all’origine e le stesse coordinate sull’ellissoide di
riferimento non supera il valore di 10–6.
200 km in planimetria
10-20 km in altimetria
Campo
Topografico
distanza entro la quale la differenza relativa tra le
coordinate di un punto su un piano tangente
all’origine e le stesse coordinate sull’ellissoide di
riferimento non supera il valore di 10–6.
15 km in planimetria
100 m in altimetria