I FONDAMENTI DELLA GEOMETRIA
EUCLIDEA
QUALE GEOMETRIA?
• SCUOLA MEDIA: geometria intuitiva
(osservazione di proprietà, applicazione di
formule...)
• SCUOLA SUPERIORE: geometria razionale
(dimostrazione di proprietà tramite
ragionamenti logici)
METODO ASSIOMATICO-DEDUTTIVO
CONCETTI PRIMITIVI
Concetti assunti come veri senza
darne una definizione,
supponendone una conoscenza
intuitiva
(punto, retta, piano)
DEFINIZIONI DI NUOVI ENTI
GEOMETRICI
(semiretta, segmento, angolo,......)
ASSIOMI O POSTULATI
Proposizioni che si accettano come
vere, senza darne una
giustificazione
(APPARTENENZA, ORDINE,
PARTIZIONE DEL PIANO)
TEOREMI
Proposizioni che esprimono
proprietà degli enti geometrici
ASSIOMI O POSTULATI
• APPARTENENZA:
1)Ogni piano è un insieme di punti;ogni retta è un sottoinsieme del piano
2)Assioma di appartenenza della retta:
a)a ogni retta appartengono almeno due punti distinti
b) dati due punti distinti, esiste una e una sola retta alla quale
appartengono entrambi
3)Assioma di appartenenza del piano:
Ogni piano contiene almeno tre punti non allineati
• ORDINE DELLA RETTA:
Tra i punti della retta è possibile introdurre due relazioni d’ordine (la retta può
essere orientata in due modi opposti)
TEOREMI
• Esprimono nuove proprietà degli enti geometrici
• Si deducono SOLO dagli assiomi o da teoremi già
dimostrati
• Sono formati da:
a)Enunciato :la frase che esprime la proprietà da
dimostrare, suddiviso in ipotesi (ciò che
supponiamo vero) e tesi (ciò che vogliamo
dimostrare)
b)Dimostrazione: il ragionamento logico che
permette di dedurre la tesi
NUOVE DEFINIZIONI
• FASCIO PROPRIO:
L’insieme delle infinite rette che passano per
un punto del piano;
il punto si chiama centro del fascio.
• FIGURA GEOMETRICA:
Ogni sottoinsieme di punti del piano
•
SEMIRETTA:
Data una retta orientata, un suo punto O individua due semirette:
O e tutti i punti che lo seguono
O e tutti i punti che lo precedono
• SEGMENTO:
Data una retta orientata e due suoi punti A e B,
Il segmento AB è l’insieme costituito da A, B e
tutti i punti compresi tra A e B
A,B=estremi, gli altri punti si dicono
interni
Segmento nullo=se A e B coincidono
• SEGMENTI CONSECUTIVI:
Due segmenti che hanno
in comune SOLO un estremo
• SEGMENTI ADIACENTI:
Due segmenti consecutivi che
appartengono alla stessa retta
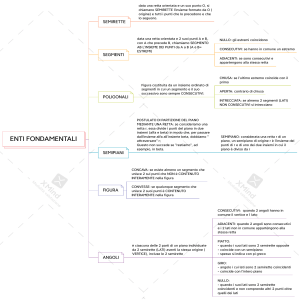
• POLIGONALE:
Insieme di segmenti:
1)consecutivi ma non adiacenti
2)segmenti non successivi non hanno estremi
in comune
Segmenti=lati; estremi=vertici
NON SONO
POLIGONALI
ABCDE=chiusa
FGHI=aperta
(1° e ultimo estremo coincidono)
(non coincidono)
JKLM=intrecciata
(lati non consecutivi hanno
un punto in comune)
FIGURA
CONVESSA
FIGURA
CONCAVA
Una figura geometrica F si dice CONVESSA se COMUNQUE si scelgano due
suoi punti, il segmento che li congiunge è tutto contenuto nella figura;
una figura non convessa si dice CONCAVA
• ASSIOMA DI PARTIZIONE DEL PIANO DA PARTE DI UNA RETTA:
Una retta divide il piano in due parti;
se prendiamo il punto A da una parte e il punto B dall’altra, allora il segmento
AB interseca la retta r in un solo punto
SEMIPIANO:
Data una retta di un piano, si chiama
semipiano la figura costituita dalla retta e
da una delle due parti in cui il piano
è diviso dalla retta stessa.
(retta= origine o frontiera del semipiano)
ANGOLO:
Date in un piano due semirette aventi la stessa origine, si chiama ANGOLO la
figura formata dalle semirette e da una delle due parti in cui il piano è diviso
dalle due semirette
Origine delle semirette= vertice
Semirette= lati
Rosso=concavo
Verde=convesso
ANGOLO PIATTO:
ogni angolo che ha
come lati una coppia di
semirette opposte
ANGOLO GIRO:
Ogni angolo che ha come lati due
semirette coincidenti e che coincide
con l’intero piano
ANGOLO NULLO:
ogni angolo che ha come lati due semirette
coincidenti e che non contiene altri punti
oltre a quelli dei suoi lati
ANGOLI CONSECUTIVI:
Due angoli si dicono consecutivi se hanno lo stesso
vertice e se hanno in comune soltanto i punti di un lato
ANGOLI ADIACENTI:
Due angoli si dicono adiacenti se sono
consecutivi e se i lati non comuni sono uno
il prolungamento dell’altro
ANGOLI OPPOSTI AL VERTICE:
Due angoli convessi si dicono opposti al vertice se i
lati dell’uno sono i prolungamenti dei lati dell’altro
ASSIOMA DI PARTIZIONE DEL PIANO:
Una poligonale chiusa non intrecciata divide il
piano in due parti (una non contiene rette-punti
interni- e una contiene rette – punti esterni)
POLIGONO:
Chiamiamo poligono la figura formata da una
poligonale chiusa non intrecciata e dai suoi punti interni
DIAGONALE:Ogni segmento che congiunge due vertici
non consecutivi
CORDA: ogni segmento che congiunge due
punti del contorno del poligono
appartenenti a due lati distinti
ANGOLO INTERNO: Ogni
angolo individuato da
due lati consecutivi del
poligono e dal vertice
comune
ANGOLO ESTERNO:
Ogni angolo adiacente a un
angolo interno del poligono
Si ottiene prolungando un lato
Per ogni vertice del poligono
ci sono esattamente DUE angoli
esterni (e un angolo interno)
In
NON E’ UN ANGOLO ESTERNO!!
(è l’opposto al vertice di quello
interno)
RIASSUMENDO............
CONCETTI PRIMITIVI
Punto, retta piano
ASSIOMI
(appartenenza, ordine,
partizione del piano)
DEFINIZIONI
Fascio proprio, figura geometrica, semiretta,
segmento, segmenti consecutivi e adiacenti,
poligonale, poligonali chiuse, aperte, intrecciate,
figure concave e convesse,
semipiano, angolo, angolo piatto, giro e nullo, angoli consecutivi, adiacenti e
opposti al vertice,
poligono, diagonale, corda, angolo interno ed esterno