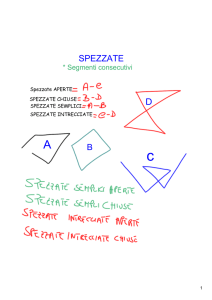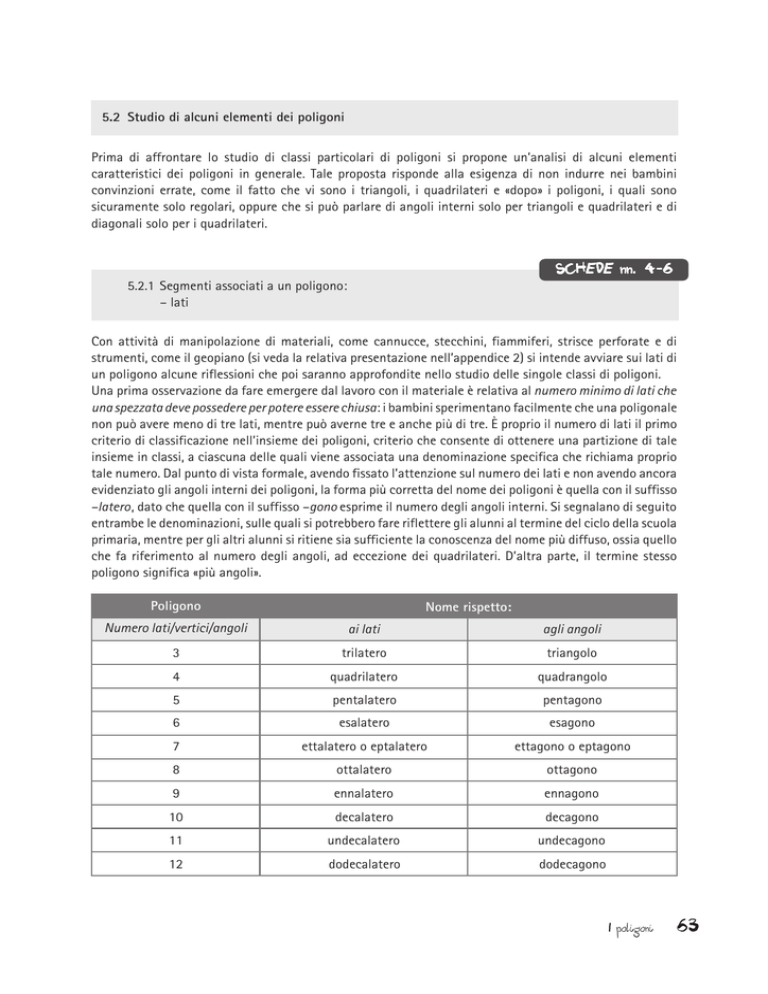
5.2 Studio di alcuni elementi dei poligoni
Prima di affrontare lo studio di classi particolari di poligoni si propone un’analisi di alcuni elementi
caratteristici dei poligoni in generale. Tale proposta risponde alla esigenza di non indurre nei bambini
convinzioni errate, come il fatto che vi sono i triangoli, i quadrilateri e «dopo» i poligoni, i quali sono
sicuramente solo regolari, oppure che si può parlare di angoli interni solo per triangoli e quadrilateri e di
diagonali solo per i quadrilateri.
SCHEDE nn. 4–6
5.2.1 Segmenti associati a un poligono:
– lati
Con attività di manipolazione di materiali, come cannucce, stecchini, fiammiferi, strisce perforate e di
strumenti, come il geopiano (si veda la relativa presentazione nell’appendice 2) si intende avviare sui lati di
un poligono alcune riflessioni che poi saranno approfondite nello studio delle singole classi di poligoni.
Una prima osservazione da fare emergere dal lavoro con il materiale è relativa al numero minimo di lati che
una spezzata deve possedere per potere essere chiusa: i bambini sperimentano facilmente che una poligonale
non può avere meno di tre lati, mentre può averne tre e anche più di tre. È proprio il numero di lati il primo
criterio di classificazione nell’insieme dei poligoni, criterio che consente di ottenere una partizione di tale
insieme in classi, a ciascuna delle quali viene associata una denominazione specifica che richiama proprio
tale numero. Dal punto di vista formale, avendo fissato l’attenzione sul numero dei lati e non avendo ancora
evidenziato gli angoli interni dei poligoni, la forma più corretta del nome dei poligoni è quella con il suffisso
–latero, dato che quella con il suffisso –gono esprime il numero degli angoli interni. Si segnalano di seguito
entrambe le denominazioni, sulle quali si potrebbero fare riflettere gli alunni al termine del ciclo della scuola
primaria, mentre per gli altri alunni si ritiene sia sufficiente la conoscenza del nome più diffuso, ossia quello
che fa riferimento al numero degli angoli, ad eccezione dei quadrilateri. D’altra parte, il termine stesso
poligono significa «più angoli».
Poligono
Nome rispetto:
Numero lati/vertici/angoli
ai lati
agli angoli
3
trilatero
triangolo
4
quadrilatero
quadrangolo
5
pentalatero
pentagono
6
esalatero
esagono
7
ettalatero o eptalatero
ettagono o eptagono
8
ottalatero
ottagono
9
ennalatero
ennagono
10
decalatero
decagono
11
undecalatero
undecagono
12
dodecalatero
dodecagono
I poligoni
63
Quando i lati, quindi gli angoli, sono più di dodici, non si hanno più nomi specifici: si dice «poligono di 13,
14, 15, … lati».
È opportuno guidare l’attività di costruzione di modelli di poligoni con domande circa la possibilità o meno,
al variare del numero di lati, di:
–
–
–
–
ottenere poligoni concavi e poligoni convessi;
ottenere modelli rigidi o modelli deformabili;
costruire il modello in relazione alle diverse lunghezze dei lati;
avere un unico poligono, una volta assegnati i lati.
In particolare, gli alunni dovrebbero rilevare che:
– i triangoli ottenuti sono sempre convessi, i modelli non sono deformabili e date tre strisce o tre cannucce,
tutti i triangoli che si possono costruire sono fra loro «uguali»;
– i poligoni con più di tre lati possono essere concavi o convessi, anzi si può «con continuità» deformare un
modello in modo da passare da un poligono concavo a uno convesso con lo stesso numero di lati;
– assegnati più di tre lati, essi possono essere uniti consecutivamente in modi differenti, per cui risultano
modelli di poligoni diversi tra loro, in quanto formati dagli stessi lati posti in ordine diverso.
È importante che l’insegnante pianifichi attentamente le attività e prepari con cura il materiale. Infatti, affinché
la costruzione dei modelli di poligoni sia possibile le lunghezze dei lati devono soddisfare la proprietà secondo cui
il lato maggiore deve avere lunghezza minore della somma delle lunghezze dei lati rimanenti. Pertanto, se non si
intende in questa prima fase fare emergere tale problematica, si devono scegliere e combinare strisce, stecchini,
cannucce di lunghezza opportuna. Una ricerca sistematica della condizione sulle lunghezze dei lati per avere la
costruibilità del poligono viene presentata per i quadrilateri (Capitolo sesto) e per i triangoli (Capitolo settimo).
Anche con il geopiano è possibile proporre la costruzione di poligoni con diverso numero di lati, concavi o
convessi, mentre viene meno la dinamicità dei modelli precedenti; proprio questa caratteristica rende il
geopiano un supporto comodo per lo studio del numero delle diagonali dei poligoni.
Nota sulla scheda n. 6
La relazione definita dalla proprietà «... ha lo stesso numero di lati di ...» ha la proprietà riflessiva, ossia ogni
poligono è in relazione con se stesso. Nella rappresentazione tramite frecce è dunque necessario segnare ogni
freccia che parte da un punto e torna sul punto stesso (cappio)
La relazione è inoltre simmetrica (coppie di frecce con verso opposto) e transitiva, quindi è una relazione di
equivalenza.
SCHEDE nn. 7–8
5.2.1 Segmenti associati a un poligono:
– diagonali
Il concetto di corda in genere viene introdotto a scuola solo nel caso del cerchio; in realtà esso ha significato
anche nel caso dei poligoni, in quanto una corda è un segmento i cui estremi appartengono a lati distinti della
poligonale che individua il poligono.
B
P
C
R
A
D
Q
F
64
NEL
MONDO DELLA GEOMETRIA
E
Nell’esagono ABCDEF
i segmenti PQ, FR, EB
sono corde.
Le diagonali sono corde aventi gli estremi in due vertici non consecutivi del poligono. Con riferimento al
poligono sopra disegnato, tra le corde rappresentate è diagonale solo il segmento EB.
Dal punto di vista didattico il lavoro sulle diagonali può essere condotto con l’utilizzo di diversi mediatori e
con differenti livelli di approfondimento, per cui si lascia all’insegnante la selezione delle attività da proporre
tra quelle di seguito suggerite, in relazione al reale contesto di insegnamento.
Una prima attività, da svolgere in piccoli gruppi in modo da aumentare il numero di verifiche condotte, è
finalizzata a fare scoprire agli alunni che il numero delle diagonali è costante per poligoni con lo stesso
numero di lati, mentre può variare la posizione delle diagonali rispetto al poligono stesso in relazione alla sua
concavità o convessità. Si suggerisce di distribuire ad ogni gruppo di bambini alcuni disegni, piuttosto grandi,
di poligoni, in modo che ogni gruppo abbia almeno un triangolo, un quadrilatero, un pentagono e un esagono
e che vi siano tipi diversi di tali poligoni (per esempio, triangoli rettangoli, acutangoli, ottusangoli, isosceli,
scaleni, equilateri; quadrilateri, pentagoni ed esagoni concavi e convessi, con o senza angoli retti o lati
congruenti o angoli congruenti). I bambini devono tracciare in ogni poligono tutte le possibili diagonali e
registrare quanto ottenuto in una tabella tipo:
Nome poligono
Poligono concavo
o convesso?
N. diagonali
N. diagonali
interne
N. diagonali
esterne
La condivisione dei risultati ottenuti consente di rilevare che:
– i triangoli non hanno diagonali;
– i poligoni con lo stesso numero di lati hanno lo stesso numero di diagonali, mentre i poligoni con diverso
numero di lati hanno anche diverso numero di diagonali;
– il numero delle diagonali è uguale al numero dei lati solo nei pentagoni;
– nei poligoni convessi tutte le diagonali sono interne, mentre nei poligoni concavi vi sono diagonali esterne;
– il numero e la posizione delle diagonali non dipende da altre caratteristiche dei poligoni.
È possibile proporre la stessa attività utilizzando, anziché il disegno su carta, la riproduzione dei poligoni sul
geopiano oppure la loro rappresentazione con il software Cabri. Inoltre, con il geopiano è interessante anche
procedere in modo inverso, ossia assegnare un segmento e richiedere di costruire alcuni poligoni che hanno
quel segmento come diagonale.
In genere, già nello svolgimento del primo lavoro proposto, indipendentemente dal supporto utilizzato, sorge
il problema della ricerca di una strategia per procedere in modo «ordinato ed esaustivo» a tracciare le
diagonali e a contarle; inoltre, qualche alunno pone la domanda sull’esistenza di una relazione tra il numero
dei lati e il numero delle diagonali, in modo da poter dire quante diagonali ha un poligono senza doverle
necessariamente tracciare.
Per affrontare le questioni emerse, si suggerisce di riprodurre, su un foglio di carta da pacco posto a terra,
un poligono, per esempio un pentagono, e di sistemare un alunno in corrispondenza di ogni vertice del
poligono. Ad un alunno viene assegnato il ruolo di tenditore di diagonali: a partire da un vertice del poligono,
il tenditore deve tendere corde di uno stesso colore verso tutti i vertici che non sono consecutivi a quello in
esame, facendo impugnare le corde ai bambini posti ai vertici; in modo analogo procede per ogni vertice,
cambiando ogni volta il colore delle corde.
I poligoni
65
Al termine della costruzione si fa osservare quante corde impugna ciascun bambino vertice (due, nel caso
del pentagono) e quante corde sono state tese in tutto (per il pentagono 2 x 5 = 10). Se non emerge
spontaneamente dagli alunni, si lancia la provocazione di assumere come numero delle diagonali proprio
il numero delle corde tese. In realtà, i bambini constatano facilmente che il numero delle diagonali è la
metà di quello delle corde tese, in quanto ogni diagonale è visualizzata da una coppia di corde tese. Per
confermare questa intuizione si può ripetere l’esperienza a partire da un esagono e, poi, rendere più
sistematica la verifica lavorando con i poligoni dai triangoli ai dodecagoni rappresentati su carta o con
Cabri oppure, in alcuni casi, costruiti sul geopiano. Le osservazioni quantitative si possono raccogliere in
una tabella come la seguente:
66
Numero lati/vertici
poligono
Numero diagonali
da ogni vertice
Numero diagonali
poligono
3
0
(0 x 3) : 2 = 0
4
1
(1 x 4) : 2 = 2
5
2
(2 x 5) : 2 = 5
6
3
(3 x 6) : 2 = 9
7
4
(4 x 7) : 2 = 14
8
5
(5 x 8) : 2 = 20
9
6
(6 x 9) : 2 = 27
10
7
(7 x 10) : 2 = 35
11
8
(8 x 11) : 2 = 44
12
9
(9 x 12) : 2 = 54
NEL
MONDO DELLA GEOMETRIA
A sua volta la tabella può essere spunto per osservazioni significative.
1. Se si mette in relazione il numero dei lati o vertici di un poligono con quello delle diagonali uscenti da
ciascun suo vertice si rileva che la differenza è sempre 3:
Numero lati/vertici
poligono
Numero diagonali
da ogni vertice
Differenza
3
0
3–0=3
4
1
4–1=3
5
2
5–2=3
6
3
6–3=3
7
4
7–4=3
8
5
8–5=3
9
6
9–6=3
10
7
10 – 7 = 3
11
8
11 – 8 = 3
12
9
12 – 9 = 3
La ragione di questa differenza costante tra il numero di vertici e il numero di diagonali uscenti da ogni
vertice sta nel fatto che i vertici con i quali non si individuano diagonali sono il vertice stesso da cui si
tracciano le diagonali e i due vertici ad esso consecutivi, con i quali vengono definiti due lati del poligono.
Se n indica il numero di lati/vertici di un poligono, la formula che generalizza quanto verificato dagli
alunni e consente di calcolare il numero d delle diagonali del poligono è:
d = (n – 3) x n
2
Pur senza arrivare alla scrittura di questa formula, con l’attività condotta i bambini hanno costruito una
procedura di calcolo che consente loro di determinare il numero di diagonali di un poligono a partire dal
numero di lati del poligono.
2. Se si mette in relazione il numero di lati/vertici e il numero di diagonali di un poligono si possono rilevare
altre regolarità. Per esempio, i bambini rilevano facilmente che il pentagono è un poligono particolare
perché il numero dei lati è uguale a quello delle diagonali , mentre nei poligoni che lo precedono (triangolo
e quadrilatero) i lati sono più numerosi delle diagonali e in quelli che lo seguono (esagono, …) i lati sono
meno numerosi delle diagonali. Inoltre, la successione del numero delle diagonali si ottiene a partire da
zero e applicando ordinatamente gli operatori +2, +3, +4, …
L’approfondimento dell’osservazione precedente circa il fatto che ogni diagonale è visualizzata da due corde
tese tra i bambini-vertici del poligono, può portare a tabulare il numero di diagonali che è necessario
tracciare da ogni vertice, in modo da avere tutte le diagonali del poligono, ma senza doppioni, ossia senza
segmenti tracciati due volte o visualizzati due volte con corde o fili. È possibile riproporre l’esperienza
motoria con le corde oppure l’esperienza manipolatoria con il geopiano, ponendo però il vincolo che da ogni
vertice si tendano solo le corde o i fili che visualizzano diagonali non già tracciate. Nel caso del pentagono,
se si procede in ordine alfabetico rispetto al nome dei vertici e si differenziano le diagonali aggiunte con il
tratto, si ha:
I poligoni
67
Prima fase
Seconda fase
B
Terza fase
B
A
B
A
C
A
C
○
○
C
○
○
○
○
○
○
○
E
D
E
D
E
○
D
La tabella che raccoglie i dati relativi ai diversi poligoni, nei quali i vertici sono denominati in ordine
alfabetico a partire da A, è
Numero diagonali «nuove» dal vertice
Poligono
N. vertici
A
B
C
triangolo
3
0
0
0
quadrilatero
4
1
1
0
0
pentagono
5
2
2
1
0
0
esagono
6
3
3
2
1
0
0
ettagono
7
4
4
3
2
1
0
0
ottagono
8
5
5
4
3
2
1
0
0
ennagono
9
6
6
5
4
3
2
1
0
0
decagono
10
7
7
6
5
4
3
2
1
0
0
undecagono
11
8
8
7
6
5
4
3
2
1
0
0
dodecagono
12
9
9
8
7
6
5
4
3
2
1
0
D
E
F
G
H
I
L
M
N
0
La tabella evidenzia che dai primi due vertici è sempre possibile tracciare il numero massimo di diagonali,
mentre dal terzo vertice il numero di diagonali «nuove» diminuisce di 1, fino agli ultimi due vertici dai quali
non vi sono diagonali da segnare oltre quelle già ottenute come uscenti da vertici precedenti.
68
NEL
MONDO DELLA GEOMETRIA
SCHEDA n. 4
Osserviamo e
riflettiamo
5.2.1 Segmenti
associati a un
poligono: lati
POLIGONI E LATI
Osserva i poligoni disegnati. Per ognuno scrivi il numero dei lati, il nome e la proprietà di essere
concavo o convesso.
ESEMPIO
6 lati
esagono
convesso
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
........................................................
Usa uno stesso colore per ripassare il contorno solo dei poligoni che hanno uguale numero di lati.
Secondo te:
– qual è il minor numero di lati che può avere un poligono? ..........................................................................................
– qual è il minor numero di lati che può avere un poligono concavo? ..................................................................
Confronta le tue risposte con quelle di un tuo compagno e discutine con l’insegnante.
© 2004, C. Colombo Bozzolo e A. Costa (a cura di), Nel mondo della geometria – volume 3, Trento, Erickson
69
Osserviamo,
riflettiamo e
rappresentiamo
SCHEDA n. 5
5.2.1 Segmenti
associati a un
poligono: lati
CLASSIFICHIAMO POLIGONI
Osserva l’insieme P di poligoni disegnato.
P
a
b
d
c
e
f
h
g
i
Completa la tabella segnando una crocetta nella casella opportuna.
poligono
triangolo quadrilatero pentagono
esagono
ettagono
ottagono
ennagono decagono
a
b
c
d
e
f
g
h
i
Tra le caselle evidenziate con una crocetta, colora di giallo quelle che corrispondono ai poligoni
concavi e di azzurro quelle che corrispondono ai poligoni convessi.
Usa gli strumenti del disegno per rappresentare sul tuo quaderno:
– un quadrilatero concavo
– un esagono convesso
– un pentagono concavo
– un decagono convesso.
70
© 2004, C. Colombo Bozzolo e A. Costa (a cura di), Nel mondo della geometria – volume 3, Trento, Erickson
Osserviamo e
riflettiamo
SCHEDA n. 6
5.2.1 Segmenti
associati a un
poligono: lati
METTIAMO IN RELAZIONE
Osserva l’insieme P di poligoni sotto disegnato. Traccia tutte le possibili frecce che rappresentano
la relazione «... ha lo stesso numero di lati di...»
P
Osserva la rappresentazione che hai ottenuto e rispondi alle seguenti domande.
– In corrispondenza di ogni poligono hai tracciato la freccia che parte e arriva al poligono
stesso? Perché?
..........................................................................................................................................................................................................................................................
..........................................................................................................................................................................................................................................................
– Per ogni freccia tracciata c’è anche quella di verso opposto? Perché?
..........................................................................................................................................................................................................................................................
..........................................................................................................................................................................................................................................................
© 2004, C. Colombo Bozzolo e A. Costa (a cura di), Nel mondo della geometria – volume 3, Trento, Erickson
71