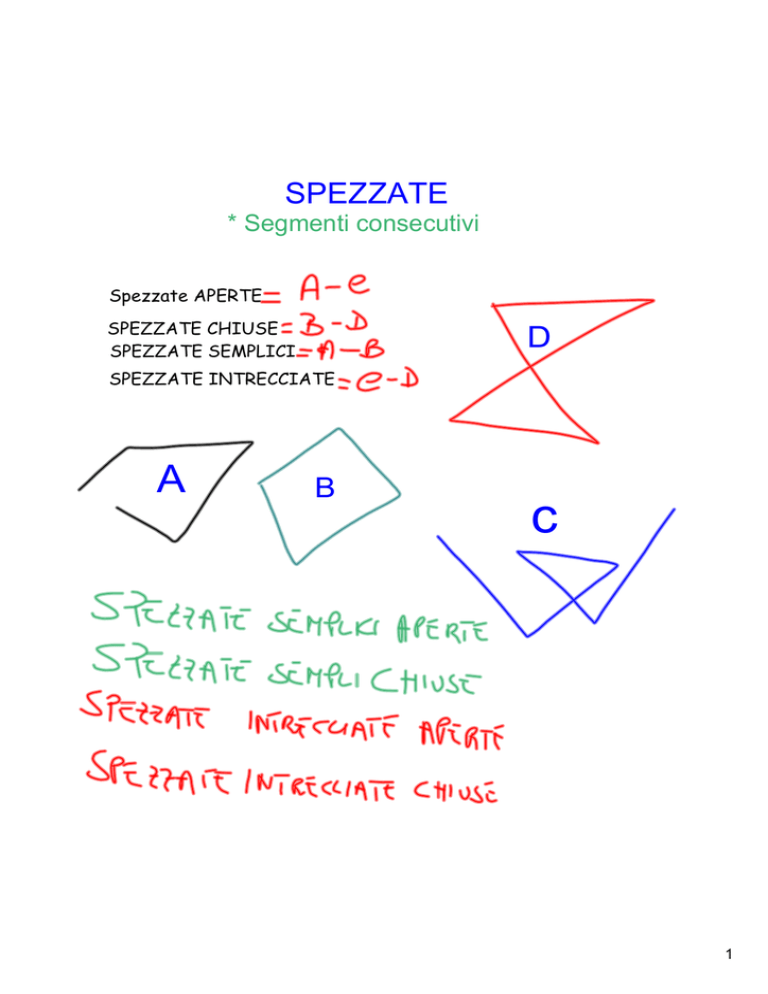
SPEZZATE
* Segmenti consecutivi
Spezzate APERTE
SPEZZATE CHIUSE
SPEZZATE SEMPLICI
D
SPEZZATE INTRECCIATE
A
B
c
1
POLIGONI
PARTE Di PIANO DELIMITATA
DA UNA SPEZZATA SEMPLICE CHIUSA
ANGOLO ESTERNO
CONTORNO
LATI
PERIMETRO
VERTICI
ANGOLI INTERNI
ANGOLO ESTERNO
FC= DIAGONALE
2
POLIGONO
CONVESSO
POLIGONO
CONCAVO
3
POLIGONI REGOLARI
4
Lezione: pag 457 e 458
Es: pag 469 n° 50 a 57
pag 464,465 n° 17 ÷ 23
5
Lezione da pag 456 a pag 458
Esercizi pag 463 e 464
dal n° 1 al n°12
pag 464,465 n° 17 ÷ 23
Es: pag 469 n° 50 a 57
6
PROPRIETA' GENERALI DEI POLIGONI
IN OGNI POLIGONO CIASCUN LATO E' SEMPRE MINORE DELLA SOMMA DI TUTTI GLI ALTRI
esiste un triangolo
con questi lati?
7
In un poligono di n lati, per ogni vertice avremo (n ­ 3) diagonali Questa proprietà ci indica quante diagonali posso tracciare da ciascun vertice, NON quante sono le diagonali del poligono
Esempio: pentagono, 5 lati:
diagonali da ogni vertice: 5 ­ 3= 2
8
In un poligono di n lati, in tutto ci sono n*(n ­3)/ 2 diagonali Esempio:
Quadrilateri: 4*(4­3)/2 = 4*1/2=2
In un esagono, quante diagonali ci sono? E in un ettagono (7 lati)?
n*(n ­3)/ 2
9
In un poligono qualsiasi
la SOMMA degli ANGOLI ESTERNI
è sempre un angolo giro, cioè misura 360°,
qualunque sia il numero dei lati.
10
In un poligono qualsiasi
la SOMMA degli ANGOLI INTERNI
è sempre (n ­ 2) ANGOLI PIATTI,
ovvero
Si = (n ­ 2) x 180°
11
Esercizi: da pag. 474 in poi;
n° 84, 85, 86, 90, 91,92,93, 94,97,98, 108,109,110 12
POLIGONI CONGRUENTI: se sovrapposti coincidono punto per punto
POLIGONI ISOPERIMETRICI: sono i poligoni che hanno lo stesso perimetro
13