Disegnare un Triangolo Rettangolo ABC , con l`angolo retto in A

Prof Tortorelli Leonardo
Skakko-Math (studenti.it)
GEOMETRIA EUCLIDEA / QUADRILATERI / Rettangolo
ESERCIZIO N°MATH.I / "CORSO MATEMATICA VERDE (LICEI NS)" - B.T.B. PG.G109.064
(“QUADRILATERI / RETTANGOLO”)
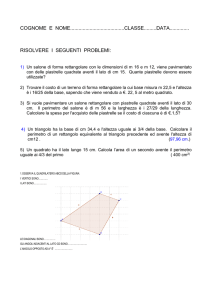
Disegnare un Triangolo Rettangolo ABC, con l’angolo retto in A. Indica con AM la mediana
relativa all’ipotenusa BC. Dimostrare che AM ha una lunghezza pari a metà di quella
dell’ipotenusa.
(Suggerimento: prolungare AM di un segmento MP  AM e considera il quadrilatero ACPB).
Rappresentazione Simbolica & Legenda
ABC :
Rappresentazione Grafica
Triangolo Rettangolo in  ;
A, M, C: Punti Allineati;
B, M, D: Punti Allineati;
AM :
Mediana Relativa Ipotenusa;
Rappresentazione delle Consegne / Thesi
1
2
AM   BC
Dimostrazione / Pianificazione
Strategia dimostrativa
Si prolunghi AM di un segmento AM  MP e considerare il quadrilatero
ACPB.
Per provare la tesi si seguiranno le seguenti sequenze:
I) Dimostrare che ACPB è un Parallelogramma;
II) Dimostrare che ACPB è un Parallelogramma con quattro angoli retti e
quindi è un Rettangolo;
III) Utilizzare la Caratterizzazione del Parallelogramma Rettangolo per
ottenere la thesi.
I)
Dimostrare che ACPB è un Parallelogramma
AM  MP (per Ipotesi)
 Diagonali di ABPC si intersecano nel loro Punto Medio 
BM  MC (perché M è Punto Medio di BC )
 [III Caratterizzazione Parallelogrammi]  ABPC Parallelogramma (*)
Prof Tortorelli Leonardo
Skakko-Math (studenti.it)
II) Dimostrare che ACPB è un Rettangolo;
 Aˆ   90 (per Ipotesi)

 II Caratterizzazione Parallelogrammi 
 ABPC Parallelogramma (per (*))  

(Angoli Opposti Congruenti)


ˆ
ˆ
ˆ
ˆ
 A  B  C  P   360
 Aˆ   Pˆ   90
 Aˆ   Pˆ   90
 Aˆ   Pˆ   90



  Bˆ   Cˆ 
  Bˆ   Cˆ 
  Bˆ   Cˆ 

ˆ


ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
 A  P   B  C   360 90  90   B  C   360 180  B  C   360
 Aˆ   Pˆ   90
 Aˆ   Pˆ   90


  Bˆ   Cˆ 
  Bˆ   Cˆ 

Bˆ   Cˆ  180
 Bˆ   Cˆ  

 90
ˆ

ˆ
2
2
 B  C   360  180  180  Bˆ   Cˆ   180
 Aˆ   Bˆ   Cˆ   Pˆ   90  ACPB Rettangolo
III ) Utilizzare la Caratterizzazione del Parallelogramma Rettangolo per ottenere la thesi.
 Proprietà del Rettangolo   Diagonali di ABPC sono Congruenti
ACPB Rettangolo  


 Proprietà del Parallelogramma   Diagonali di ABPC si tagliano a metà
 AM  MP  BM  MC (per Ipotesi)
(perché M è Punto Medio di dei due segmenti congruenti AP e BC )
 AM 
BM  MC BC

2
2
 AM  BM  MC 
[c.v.d.]