1
Collegamento di resistenze
Resistenze in serie
Vogliamo calcolare la resistenza elettrica del circuito ottenuto collegando tra loro più resistenze in
serie.
Colleghiamo a una pila di forza elettromotrice f.e.m. tre resistenze in serie come illustrato in figura.
Ciascuna resistenza è percorsa dalla stessa corrente. Se una resistenza elettrica si interrompe, il
circuito si apre e in esso non passa più corrente.
La differenza di potenziale tra A e D è data dalla somma delle differenze di potenziale ai capi di
ciascuna resistenza: ∆VAD = ∆VAB + ∆VBC + ∆VCD =
?V
R1 · i + R2 · i + R3 · i = (R1 + R2 + R3) · i. Quindi le
?V
?V
?V
tre resistenze in serie si comportano come un’unica
R
resistenza equivalente Re di valore pari alla loro
R
R3
1
2
somma:
Re = R1 + R2 + R3
A
D
B
C
Se invece di tre si ha un numero qualsiasi di resistenze
la regola precedente si generalizza nel seguente modo:
i
La resistenza equivalente di più resistenze
f.e.m
collegate in serie è data dalla somma di ciascuna di
.
esse.
AD
AB
BC
CD
Resistenze in parallelo
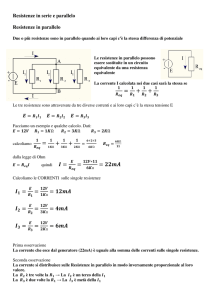
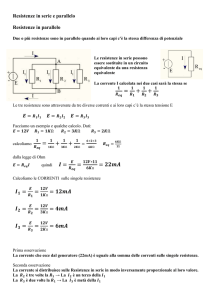
Colleghiamo ora tre resistenze in parallelo. Le estremità delle resistenze in cui entrano le correnti
sono collegate tra loro e formano il nodo A. Così pure le estremità da cui escono le correnti sono
collegate tra loro e formano il nodo B. In questo modo le resistenze si trovano alla stessa differenza
di potenziale: ∆VAB = ∆V1 = ∆V2 = ∆V3. Nel nodo A la corrente i prodotta dal generatore si
suddivide nelle correnti uscenti i1, i2, i3 che passano nelle resistenze.
Osserviamo che deve valere la relazione: i − i1 − i2 − i3 = 0, ossia la somma delle correnti entranti in
un nodo e delle correnti uscenti è nulla (“Legge dei nodi”). Se infatti così non fosse, poiché la
corrente è definita come la quantità di carica che attraversa la sezione di un conduttore nell’unità di
tempo, avremmo un accumulo o una diminuzione della carica nel nodo, contraddicendo in tal modo
il principio di conservazione della carica elettrica.
∆V
∆V AB
∆V AB
Le correnti che attraversano ciascuna resistenza sono: i1 = AB ; i2 =
; i3 =
. Inoltre, se
R1
R2
R3
sostituiamo al gruppo delle tre resistenze un’unica resistenza equivalente Re vale la relazione:
∆V AB
∆V AB ∆V AB ∆V AB
∆V AB
i=
e, poiché i = i1 + i2 + i3 possiamo scrivere:
=
+
+
.
Re
Re
R1
R2
R3
Semplifichiamo entrambi i membri per ∆VAB e otteniamo:
1
1
1
1
=
+
+ .
Re R1 R2 R3
Osserviamo che, contrariamente a quanto accade nel collegamento in serie, la resistenza equivalente
di più resistenze in parallelo è minore di ciascuna resistenza. Se invece di tre si ha un numero
qualsiasi di resistenze la regola precedente si generalizza nel seguente modo:
l’inverso della resistenza equivalente di più resistenze collegate tra loro in parallelo è data
dalla somma degli inversi di ciascuna resistenza.
2
Esempio 1 - Calcolo della resistenza equivalente di collegamenti di resistenze in serie e in parallelo
Date tre resistenze: R1 = 15,0 Ω, R2 = 20,0 Ω, R3 = 30,0 Ω, vogliamo calcolare la resistenza equivalente Re
rispettivamente:
a) nel collegamento in serie delle resistenze;
b) nel loro collegamento in parallelo.
Un generatore con f.e.m. = 130,0 V e resistenza interna trascurabile alimenta ciascun collegamento.
Vogliamo determinare la caduta di potenziale ai capi di ogni resistenza nel collegamento in serie, e
l’intensità della corrente che circola in ogni resistenza nel collegamento in parallelo.
Scriviamo i dati del problema
Valori delle resistenze: R1 = 15,0 Ω, R2 = 20,0 Ω, R3 = 30,0 Ω.
Forza elettromotrice del generatore: f.e.m. = 130,0 V
Incognite
Resistenza equivalente Re nel collegamento in serie delle tre resistenze.
Resistenza equivalente Re nel loro collegamento in parallelo.
Le cadute di potenziale ai capi di ciascuna resistenza nel collegamento in serie: ∆V1, ∆V2, ∆V3.
L’intensità della corrente in ogni resistenza nel collegamento in parallelo: i1, i2, i3.
Analisi e soluzione
Collegamento in serie: Re = 15,0 Ω + 20,0 Ω + 30,0 Ω = 65,0 Ω.
Collegamento
Re =
in
parallelo:
1
1
1
1
9,0
=
+
+
=
;
Re 15,0 Ω 20,0 Ω 30,0 Ω
60,0 Ω
otteniamo
quindi:
60,0 Ω
= 6,7 Ω .
9,0
Per calcolare la caduta di potenziale in ogni resistenza nel collegamento in serie, calcoliamo dapprima la
corrente che passa nelle resistenze: i =
f .e.m. 130,0 V
=
= 2,0 A . Otteniamo quindi:
Re
65,0 Ω
∆V1 = R1 ·i = 15,0 Ω · 2,0 A = 30,0 V; ∆V2 = R2 ·i = 20,0 Ω · 2,0 A = 40,0 V; ∆V3 = R3 ·i = 30,0 Ω · 2,0 A =
60,0 V.
La somma delle cadute di potenziale nelle tre resistenze è pari alla f.e.m. del generatore.
Calcoliamo ora le correnti che passano nelle resistenze collegate in parallelo:
i1 =
130,0 V
130,0 V
130,0 V
= 8,6 A ; i2 =
= 6,5 A ; i3 =
= 4,3 A .
15,0 Ω
20,0 Ω
30,0 Ω
La somma delle tre correnti è di 19,4 A, valore uguale alla corrente erogata dal generatore:
i =
130,0 V
= 19,4 A .
6,7 Ω
Collegamento misto
Le resistenze possono essere collegate anche in altri modi: per esempio, nel caso di tre resistenze, si
possono collegare in serie alla prima le altre due in parallelo tra di loro,
R2
come illustrato in figura. Per ottenere la resistenza equivalente
R1
dobbiamo dapprima calcolare la resistenza equivalente R2-3 del
1
1
1 . Quindi
R
parallelo tra R2 e R3 mediante la formula
=
+
3
R2 – 3 R2 R3
determiniamo la resistenza equivalente del collegamento in serie tra R1
e R2-3 : Re = R2-3 + R1.
Se invece R2 e R3 sono in serie tra loro e in parallelo con R1 come mostrato
in figura, per calcolare la resistenza equivalente del sistema dobbiamo
determinare la resistenza equivalente R2-3 della serie tra R2 e R3 con la
formula R2-3 = R2 + R3 , quindi calcolare la resistenza equivalente del
R1
R2
R
3
3
parallelo tra R1 e R2-3: 1 = 1 + 1 . Il valore della resistenza equivalente Re è dato dall’inverso del
Re R2 – 3 R1
risultato della precedente relazione.
Gli strumenti che misurano la differenza di potenziale e l’intensità di corrente
Lo strumento che misura la differenza di potenziale tra due punti, A e B, di un circuito elettrico è il
voltmetro, il cui simbolo utilizzato negli schemi elettrici è:
I morsetti del
voltmetro sono contrassegnati rispettivamente dal segno
“+” (positivo) e dal
segno “−” (negativo). Il voltmetro deve essere inserito in parallelo rispetto al ramo del circuito
compreso tra i due punti A e B in modo che il morsetto positivo sia collegato al punto del circuito a
potenziale maggiore, mentre il morsetto negativo va collegato al punto a potenziale minore.. La
resistenza del voltmetro deve essere elevata, in modo che la corrente
che lo attraversa sia trascurabile rispetto alla corrente del circuito e
non vengano alterate le caratteristiche del circuito stesso.
Lo strumento che misura l’intensità di corrente è l’amperometro, il cui
simbolo è:
I morsetti dell’amperometro sono contrassegnati rispettivamente dal
segno “+” e dal segno “−”; esso deve essere inserito in serie nel circuito per poter
essere attraversato dalla corrente che deve misurare. Il morsetto positivo viene
collegato al punto del circuito a potenziale maggiore, mentre il morsetto negativo al punto a
potenziale minore.. La resistenza interna dell’amperometro deve essere molto piccola in modo che
la caduta di potenziale ai capi della propria resistenza interna sia
trascurabile rispetto alla differenza di potenziale applicata al circuito.
4
Collegamenti di resistenze nel quotidiano
L’illuminazione dell’albero di natale o del presepe, o del profilo di monumenti, sono esempi del
collegamento in serie di resistenze elettriche. Un filo che illumina l’albero di Natale è formato da un certo
numero di lampadine collegate in serie. La somma delle differenze di potenziale applicate a ogni lampadina
dà il valore della tensione a cui è alimentato l’intero circuito. Se però una lampadina si brucia, il circuito si
apre e tutte quante le lampadine si spengono. Per ovviare a questo fatto, in parallelo a ogni lampadina è
collegata una resistenza (shunt) che interviene evitando l’interruzione del circuito.
Il circuito elettrico domestico (rete domestica) è un esempio di collegamento in parallelo di più utilizzatori.
Dal contatore che misura l’energia utilizzata dall’impianto, si diramano i fili conduttori che raggiungono le
varie stanze della casa. Collegati in parallelo a questi fili conduttori sono poste le prese elettriche fissate nei
muri. A queste prese vengono inserite le spine dei vari elettrodomestici che risultano così collegati in
parallelo alla comune differenza di potenziale di 220 V. Lo spegnimento di uno qualunque degli
elettrodomestici non interrompe il funzionamento degli altri.
5
Verifiche di comprensione
1. Qual è la caratteristica della corrente che percorre più resistenze collegate in serie?
2. Che cosa succede se una delle resistenze in serie si interrompe?
3. Da che cosa è data la differenza di potenziale totale ai capi delle resistenze in serie?
4. Come si calcola la resistenza equivalente di più resistenze collegate in serie?
5. Come si effettua il collegamento di più resistenze in parallelo?
6. Come sono le differenze di potenziale delle resistenze collegate in parallelo?
7. Che cosa afferma la legge dei nodi?
8. Come si calcola l’inverso della resistenza equivalente di più resistenze in parallelo?
9. Qual è lo strumento che misura la differenza di potenziale tra due punti di un circuito elettrico?
10. Qual è lo strumento che misura l’intensità di corrente?
11. Come si inserisce in un circuito un voltmetro?
12. Come si inserisce in un circuito un amperometro?
13. Come deve essere la resistenza interna del voltmetro e perché?
14. Come deve essere la resistenza interna dell’amperometro e perché?
15. Descrivi un esempio di realizzazione del collegamento di più resistenze in serie.
16. Come sono collegati gli elettrodomestici all’impianto elettrico?
17. A che cosa serve l’interruttore elettromeccanico in un circuito elettrico?
18. A che cosa serve l’interruttore differenziale in un circuito elettrico?
Verifiche di conoscenza
1. La resistenza equivalente di più resistenze collegate in serie è:
a. maggiore di ciascuna resistenza
b. minore di ciascuna resistenza
c. uguale alla resistenza maggiore
d. può essere minore o maggiore delle resistenze collegate, in base al loro valore
2. La resistenza equivalente di più resistenze collegate in parallelo è:
a. maggiore di ciascuna resistenza
b. minore di ciascuna resistenza
c. uguale alla resistenza maggiore
d. può essere minore o maggiore delle resistenze collegate, in base al loro valore
3. Se più resistenze sono collegate in serie, le cadute di potenziale di ciascuna resistenza sono:
a. uguali tra loro
b. uguali alla differenza di potenziale applicata al gruppo delle resistenze
c. direttamente proporzionali alla rispettiva resistenza
d. inversamente proporzionali alla rispettiva resistenza
4. Le correnti che attraversano delle resistenze collegate in parallelo sono:
a. uguali tra loro e pari alla corrente totale divisa per il numero delle resistenze
b. uguali tra loro e dello stesso valore della corrente totale
c. direttamente proporzionali alla rispettiva resistenza
d. inversamente proporzionali alla rispettiva resistenza
5. Se si collegano due resistenze a una pila, in quale situazione la corrente che attraversa la pila è
maggiore?
a. nel collegamento in serie in quanto la corrente non deve dividersi in più rami
b. nel collegamento in parallelo perché la resistenza di questo è minore del collegamento in serie
c. poiché le resistenze sono le stesse, la corrente è la stessa rispetto ai due tipi di collegamento
d. dipende dal rapporto tra le resistenze
6. La legge dei nodi afferma che
a. la somma del numero delle correnti che entrano in un nodo è uguale alla somma del numero
delle correnti che escono
b. la somma delle correnti che entrano in un nodo è uguale alla somma delle correnti che escono
c. la somma del numero delle correnti che attraversano un nodo è zero
7. In quale caso si ha il cortocircuito?
a. quando un utilizzatore è troppo vicino al generatore per cui la corrente possiede tutta la sua
efficacia e può danneggiarlo
b. quando il filo di fase entra direttamente in contatto con il filo neutro
6
c. quando un generatore eroga una potenza insufficiente per poter far funzionare gli utilizzatori
collegati, per cui il circuito si interrompe
Problemi
1. Una pila con f.e.m. di 12,0 V alimenta un circuito costituito da tre resistenze collegate in serie. I valori
delle resistenze sono rispettivamente: R1 = 10,0 Ω, R2 = 12,0 Ω, R3 = 18,0 Ω. Calcola la resistenza
equivalente del circuito, la corrente che passa nelle tre resistenze e la caduta di potenziale in ogni
resistenza.
2. Le tre resistenze: R1 = 120,0 Ω; R2 = 75,0 Ω; R3 = 150,0 Ω, sono collegate tra loro in parallelo e soggette
alla differenza di potenziale di 300,0 V. Calcola la resistenza equivalente del circuito, l’intensità totale
della corrente e l’intensità in ogni resistenza.
3. Una differenza di potenziale di 220 V alimenta 22 lampadine collegate in serie. Ogni lampadina ha una
resistenza interna di 12,5 Ω. Calcola la corrente che circola nelle lampadine e la differenza di potenziale
ai capi di ciascuna lampadina.
4. La differenza di potenziale applicata a tre resistenze in serie vale 48,0 V e la corrente che le attraversa è
di 0,2 A. Sapendo che la prima resistenza vale 100 Ω, la seconda 60 Ω, quanto vale la terza resistenza?
5. Tre resistenze sono collegate in serie e due di esse valgono rispettivamente: R1 = 12,0 Ω; R2 = 18,0 Ω. La
differenza di potenziale applicata alla prima resistenza, R1 , è di 7,20 V. Calcola la differenza di
potenziale ai capi di R2 e il valore della terza resistenza sapendo che la differenza di potenziale ai capi
dell’intero circuito è di 24,0 V.
6. Consideriamo quattro resistenze collegate in parallelo tra loro: R1 = 50,0 Ω; R2 = 75,5 Ω; R3 = 64,0 Ω; R4
= 42,5 Ω. La differenza di potenziale ai capi del collegamento è di 50,0 V. Calcola la resistenza
equivalente delle quattro resistenze e l’intensità di corrente in ciascuna di esse.
7. Una resistenza di 10,0 Ω è collegata in serie a due resistenze rispettivamente di 24,0 Ω e di 16,0 Ω
collegate tra loro in parallelo. Il circuito è alimentato da una pila di f.e.m. pari a 98,0 V. Calcola la
resistenza equivalente del circuito, l’intensità della corrente erogata dalla pila e l’intensità delle correnti
che passano attraverso le due resistenze in parallelo.
8. Determina la resistenza da collegare in parallelo a una resistenza di 240 Ω in modo da ottenere una
resistenza equivalente di 80 Ω.
9. Determina quante resistenze da 60,0 Ω occorre collegare in parallelo a una pila la cui f.e.m. vale 240 V,
affinché la corrente totale sia di 12 A.