I.C. Scarpa - Scuola media Cairoli
ISTRUZIONI PER INIZIARE
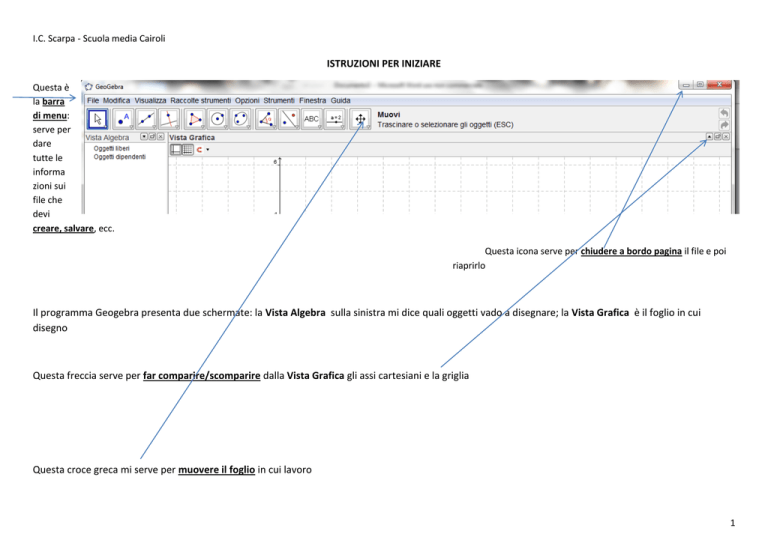
Questa è
la barra
di menu:
serve per
dare
tutte le
informa
zioni sui
file che
devi
creare, salvare, ecc.
Questa icona serve per chiudere a bordo pagina il file e poi
riaprirlo
Il programma Geogebra presenta due schermate: la Vista Algebra sulla sinistra mi dice quali oggetti vado a disegnare; la Vista Grafica è il foglio in cui
disegno
Questa freccia serve per far comparire/scomparire dalla Vista Grafica gli assi cartesiani e la griglia
Questa croce greca mi serve per muovere il foglio in cui lavoro
1
I.C. Scarpa - Scuola media Cairoli
PUNTI
Quando apri il programma Geogebra ti si presenta questa schermata:
Nome del programma
Simbolo del puntatore
Punto
Se con il tasto sinistro del mouse clicchi sul simbolo Punto il fondo del simbolo cambia colore: vuol dire che stai usando questa funzione, cioè puoi disegnare un
punto.
Clicca in un punto qualunque del foglio (Vista Grafica): comparirà un punto con il suo nome scritto in maiuscolo (A, perché è il primo punto) e nella parte sinistra
dello schermo (Vista Algebra) comparirà il nome del punto e le sue coordinate nel piano cartesiano.
Ora disegna almeno 4 punti, vai su Puntatore, “afferra” i punti e trascinali
Clicca con il tasto destro del mouse sul punto A; ti comparirà questo menu a tendina:
Mostra oggetto ti consente di nascondere il punto e poi, se vuoi, cliccando una seconda volta, farlo ricomparire
Mostra etichetta ti permette di far scomparire e poi riapparire l’etichetta con il nome del punto.
Rinomina ti permette di cambiare il nome del punto (ricorda, sempre maiuscolo).
Elimina ti consente di cancellare definitivamente il punto
2
I.C. Scarpa - Scuola media Cairoli
Il tasto Proprietà ti consente di fare molte funzioni. Quando clicchi su questo tasto si apre una finestra come questa:
Togliendo la spunta, puoi:
Scegliere di non mostrare il punto(mostra oggetto);
Scegliere di mostrare l’etichetta con il valore (cioè le coordinate) del punto;
Andare nel menu Colore e cambiare il colore del punto (MENU COLORE)
Ora esercitati a disegnare 6 punti,
a colorarli in modo diverso,
a cambiare il loro aspetto,
a spostarli
a far comparire le loro coordinate cartesiane come
nell’esempio
SEGMENTI
Clicca sul menu Retta, ti comparirà questa finestra:
Scegli la funzione Segmento tra due punti e disegna un segmento AB
3
I.C. Scarpa - Scuola media Cairoli
Disegna ora altri 2 segmenti CD ed EF tutti separati come in figura:
Nella finestra Vista Algebra il computer ti informa che hai costruito i tre segmenti a, b, c
e ti dice la loro lunghezza
Clicca su Puntatore e rendi i segmenti consecutivi, come in figura:
4
I.C. Scarpa - Scuola media Cairoli
ANGOLI
Costruisci una semiretta di origine nel punto A e passante per un punto B
Costruisci una seconda semiretta sempre di origine in A e passante per il punto C
Clicca sull’icona Opzioni della barra di menu e, quando compare la finestra di dialogo, clicca su Arrotondamento
Scegli 0 cifre decimali
Ora clicca sull’icona Angolo e
costruisci l’angolo CAB, cliccando sui punti in quest’ordine
Se hai lavorato correttamente ti compare l’ampiezza dell’angolo CAB senza decimali
Vai su Puntatore e sposta il punto C disegnando:
o Un angolo acuto
o Un angolo retto
o Un angolo ottuso
o Un angolo piatto
o Un angolo concavo
o Un angolo giro
Scrivi in una casella di testo l’ampiezza di ciascuno degli angoli disegnati
5
I.C. Scarpa - Scuola media Cairoli
ANGOLI OPPOSTI AL VERTICE
Disegna due rette incidenti nel punto A
Disegna un punto D sulla semiretta opposta alla semiretta AB
Disegna un punto E sulla semiretta opposta alla semiretta AC
Disegna gli angoli CAD e EAB nell’ordine dato.
Come sono tra loro i due angoli?
Scrivi e completa in una casella di testo: “Due angoli opposti al vertice sono tra loro……..”
6
I.C. Scarpa - Scuola media Cairoli
RETTE
Disegna due punti A e B
Costruisci la retta passante per questi due punti
Con la funzione Retta Perpendicolare costruisci la retta perpendicolare alla retta AB e passante per A
Costruisci la retta perpendicolare ad AB e passante per B
Come sono tra loro le due rette?..........................................
Scrivi in una casella di testo la seguente affermazione, completandola: “due rette perpendicolari ad una terza retta sono tra
loro……..”
ASSE DI UN SEGMENTO
Costruisci un segmento AB, coloralo come vuoi e cambiane lo spessore
Costruisci l’asse di questo segmento
Costruisci un punto C sull’asse del segmento
Clicca sul pulsante della barra di menu che ti permette di calcolare l’ampiezza degli angoli, la lunghezza di segmenti, l’area delle
figure
Calcola la distanza AC e AB.
Sposta il punto C. Cosa noti?...................................................................
Scrivi una casella di testo completando: “l’asse di un segmento è una retta ……………………………………al segmento e passante per il
suo punto…………………………. Tutti i punti appartenenti all’asse sono…………………………dagli………………………..del segmento stesso”
7
I.C. Scarpa - Scuola media Cairoli
SEGMENTO DI DATA LUNGHEZZA
Disegna un segmento AB di lunghezza 6 con la funzione Segmento dati un punto e la lunghezza
Clicca su uno degli estremi, clicca con il
tasto destro del mouse, scegli Proprietà e spunta Mostra traccia
Ora vai su Puntatore e muovi uno
degli estremi
Cosa
compare?????....................................................................
8
I.C. Scarpa - Scuola media Cairoli
TRIANGOLI
Disegna una retta parallela all’asse delle ascisse (quello orizzontale) che dista dall’asse 7 unità.
Disegna i punti di coordinate: A = (2; 1) B = (7; 1)
Con l’icona Punto su un Oggetto disegna il punto C = (3; 7) che appartiene alla retta parallela
Con la funzione Poligono costruisci il triangolo cliccando prima in A, poi in B e infine in C, poi ricordati di “chiudere” il poligono cliccando ancora in A
Nella Vista Algebra ti compare la lunghezza dei lati del triangolo (denominati dal programma rispettivamente a, b, c) e la lunghezza del perimetro del triangolo
chiamato poli1 (poligono 1, perché è il primo poligono che hai disegnato).
I triangoli possono essere classificati secondo i lati in:
Scaleni……………………………………………
Isosceli……………………………………………….
Equilateri……………………………………..
9
I.C. Scarpa - Scuola media Cairoli
I triangoli possono essere classificati secondo gli angoli in:
Acutangoli…………………………………………….
Ottusangoli………………………………….
Rettangoli……………………………………..
o
Ora chiedi al programma di calcolare l’area del triangolo con la funzione Area
o
Sposta il vertice C lungo la retta parallela all’asse delle ascisse.
o
Cosa succede al perimetro dei triangoli? Varia o rimane invariato?
o
Cosa succede all’area dei triangoli? Varia o rimane invariata?
o
Scrivi la seguente casella di testo, completandola: “I triangoli disegnati hanno tutti la stessa…………………………….., perciò si
dicono equivalenti. Triangoli equivalenti non hanno lo stesso…………………………………………………, perciò non sono isoperimetrici”.
o
10
I.C. Scarpa - Scuola media Cairoli
COSTRUZIONE DI UN TRIANGOLO DATA LA MISURA DEI LATI
Prova a costruire tre segmenti AB, BC e AC di lunghezza rispettivamente 8cm, 5 cm e 3 cm
o
Con la funzione Segmento – dato un punto e la lunghezza, 8 cm, uno di 5 cm e uno di 3 cm
o
o
o
o
o
o
o
Clicca sul pulsante Puntatore e sposta i vertici in modo che A coincida con C e F coincida con B
Sposta i vertici D ed E in modo da cercare di costruire un triangolo. Ci riesci?.................................
Calcola la somma dei due lati minori:……………………….Come è rispetto al lato maggiore?
Ora prova a costruire un triangolo con tre segmenti di lunghezza 12cm, 6 cm e 8 cm
Riesci a disegnare il triangolo?.................................
Calcola la somma dei due lati minori:……………………….Come è rispetto al lato maggiore?
Ora prova a costruire un triangolo con tre segmenti di lunghezza 12cm, 10 cm e 8 cm
11
I.C. Scarpa - Scuola media Cairoli
o
o
o
o
Riesci a disegnare il triangolo?.................................
Calcola la somma dei due lati minori:……………………….Come è rispetto al lato maggiore?
Prova ora a completare la seguente affermazione e scrivila in una casella di testo: E' possibile costruire un triangolo solo se la somma di due lati è ………………….dell'altro
lato
Calcola la differenza dei lati e verifica che puoi costruire il triangolo se la differenza di due lati è minore del terzo lato Completa la seguente tabella:
Lato a (cm) Lato b (cm) Lato c (cm) b + c a – b oppure b - c Puoi costruire il triangolo?
14
7
5
21
13
9
16
11
5
15
9
8
13
8
4
11
7
5
12
9
5
17
9
8
20
13
9
COSTRUZIONE DI UN TRIANGOLO RETTANGOLO
o
o
o
Prova a costruire un triangolo rettangolo "a occhio"
Verifica che, spostando i suoi vertici, non si mantengono le caratteristiche.
Verifica che, se invece prima disegni il segmento AB e poi utilizzi la funzione Retta Perpendicolare, anche spostando i vertici, si mantengono le caratteristiche
dell'angolo retto:
12
I.C. Scarpa - Scuola media Cairoli
COSTRUZIONE DI UN TRIANGOLO ISOSCELE
o
o
o
o
o
o
o
o
o
o
o
o
Disegna un nuovo triangolo isoscele “a occhio”
Sposta i vertici e verifica che non si mantengono le caratteristiche.
Disegna un segmento AB
Costruisci l’asse di questo segmento
Con la funzione Punto su un oggetto disegna un punto C sull’asse
Nella Vista Grafica verifica che i segmenti a1 e b1 (i lati del triangolo) sono congruenti
Misura l’ampiezza degli angoli al vertice CAB e CBA sono congruenti (ricordati che, per misurare l’ampiezza di un angolo, devi cliccare sull’icona Angolo e poi cliccare
sui tre punti nell’ordine dato)
Disegna il punto H nell’intersezione tra l’asse e il lato AB
Verifica che gli angoli ACH e BCH sono congruenti
Scrivi in una casella di testo le seguenti affermazioni, completandole:
“I triangoli isosceli hanno i lati obliqui tra loro ……………………………….. e gli angoli alla base …………………………………... L’altezza relativa alla base è
anche………………………………..dell’angolo al vertice”.
o
13
I.C. Scarpa - Scuola media Cairoli
COSTRUZIONE DELLE ALTEZZE DI UN TRIANGOLO E DEL LORO PUNTO DI INTERSEZIONE
o
o
Con la funzione Poligono disegna un triangolo ABC
Colora in rosso il perimetro del triangolo e aumenta
RICORDA: l’altezza relativa ad un lato è il segmento………………al lato e uscente dal vertice…………..
o
o
o
o
o
Con il comando Rette perpendicolari costruisci la retta perpendicolare al lato AB
Ripeti la costruzione per la retta perpendicolare al lato AC e passante per il vertice B
Ripeti la costruzione per la retta perpendicolare al lato BC e passante per il vertice A
Con il comando Punto/Intersezione di due oggetti segna il punto di intersezione delle tre rette disegnate;
RICORDA: il punto di intersezione delle altezze
si chiama:
□
baricentro
□ ortocentro
o
o
□
incentro
□
circocentro
Scegli il comando Puntatore e avvicinati ad un vertice; modifica il triangolo in modo che sia acutangolo, poi rettangolo e infine ottusangolo
Verifica dove cade l’ortocentro in ciascun triangolo e compila la tabella:
L’ortocentro è
Interno
Esterno
Coincide con un vertice
Triangolo
14
I.C. Scarpa - Scuola media Cairoli
Triangolo
Acutangolo
Triangolo
Rettangolo
Triangolo
Ottusangolo
Salva il file con il nome “altezze triangoli”
COSTRUZIONE DELLE BISETTRICI DI UN TRIANGOLO
o
o
Costruisci un triangolo ABC con il pulsante Poligono
Traccia la bisettrice dell’angolo BAC con il comando Bisettrice e cliccando sui vertici B, A, C nell’ordine dato
o Traccia la bisettrice dell’angolo ABC con il comando Bisettrice e cliccando sui vertici A, B, C nell’ordine dato
o Traccia la bisettrice dell’angolo BCA con il comando Bisettrice e cliccando sui vertici B, C, A nell’ordine dato
o Clicca sul pulsante Intersezione di due oggetti e costruisci il punto di intersezione delle bisettrici, cliccando su ciascuna
delle due bisettrici
? Come si chiama questo punto?
□ ortocentro
□ baricentro
□ incentro
□ circocentro
o
Prova a spostare i vertici A, poi B e quindi C dopo aver selezionato Puntatore.
15
I.C. Scarpa - Scuola media Cairoli
o
L’incentro è
Verifica dove cade l’incentro in ciascun triangolo e compila la tabella:
Interno
Esterno
Coincide con un vertice
Triangolo
Triangolo
Acutangolo
Triangolo
Rettangolo
Triangolo
Ottusangolo
Salva il file con il nome “bisettrici triangoli”
FACOLTATIVO
o
o
o
Continua sullo stesso file
Chiama I il punto di intersezione delle bisettrici
Con il comando Mostra/nascondi nascondi le bisettrici: ti resterà solo il punto I
16
I.C. Scarpa - Scuola media Cairoli
o
o
o
o
Costruisci la retta passante per I e perpendicolare al lato AB con il comando Retta perpendicolare
Costruisci il punto di intersezione tra questa retta e il lato AB con il comando Intersezione di due oggetti
Chiama H questo punto di intersezione
Costruisci il segmento IH con il comando Segmento
o
o
Costruisci la circonferenza con centro in I e raggio IH con il comando Circonferenza
Nascondi la retta IH con il comando Mostra nascondi
o
Sposta prima il vertice A, poi B,
infine C dopo aver selezionato Puntatore
? Che caratteristiche ha la circonferenza disegnata?……………………………...
Per quali punti passa la circonferenza?……………………………………
……………………………………………
o Indica con le lettere L e M i punti in cui la circonferenza tocca i lati del triangolo
o Come sono tra loro i segmenti IL, IM e IH?.................................................................
Verificalo guardando la Vista Grafica
Salva il file con il nome "Circonferenza inscritta"
17
I.C. Scarpa - Scuola media Cairoli
Unità 10 - COSTRUZIONE DEGLI ASSI DI UN TRIANGOLO E DEL LORO PUNTO DI INTERSEZIONE
o Costruisci un triangolo ABC
o
Seleziona il comando Asse e costruisci l’asse del lato AB
o Costruisci poi gli assi dei lati AC e BC
o Con il comando Intersezione di due oggetti clicca sul punto di intersezione degli assi e chiamalo O
RICORDA: il punto di intersezione degli assi si chiama:
o
□ ortocentro
□ baricentro
□ incentro
□ circocentro
Scegli il comando Puntatore e avvicinati ad un vertice; modifica il triangolo in modo che sia acutangolo, poi rettangolo e infine ottusangolo
Verifica dove cade il circocentro in ciascun triangolo e compila la tabella:
Il circocentro è
Interno
Esterno
Coincide con un vertice
Triangolo
Triangolo
Acutangolo
Triangolo
Rettangolo
Triangolo
Ottusangolo
18
I.C. Scarpa - Scuola media Cairoli
PER I PIU’ BRAVI
con il comando Segmenti costruisci i segmenti OA, OB, OC
con il comando Mostra-nascondi cancella gli assi
con il comando Circonferenza costruisci la circonferenza con centro O e raggio OA
o
o
Per quali punti passa la circonferenza?……………………
Come sono tra loro i segmenti OA, OB e OC?………………………………Perché?………..
Salva il file con il nome “asse di triangoli”
ESERCIZIO: ricordando che la mediana di un triangolo è un segmento che unisce un vertice con il punto medio del lato opposto,
o
o
o
o
o
costruisci un triangolo ABC
costruisci i punti medi dei lati AB, AC e BC
chiama rispettivamente L, M, N questi punti
costruisci i segmenti Cl, BM, AN
verifica deformando il triangolo se il punto di intersezione delle mediane che si chiama……………………….. è interno al triangolo.
19












