Esercitazione VIII - Lavoro ed energia II
Forze conservative
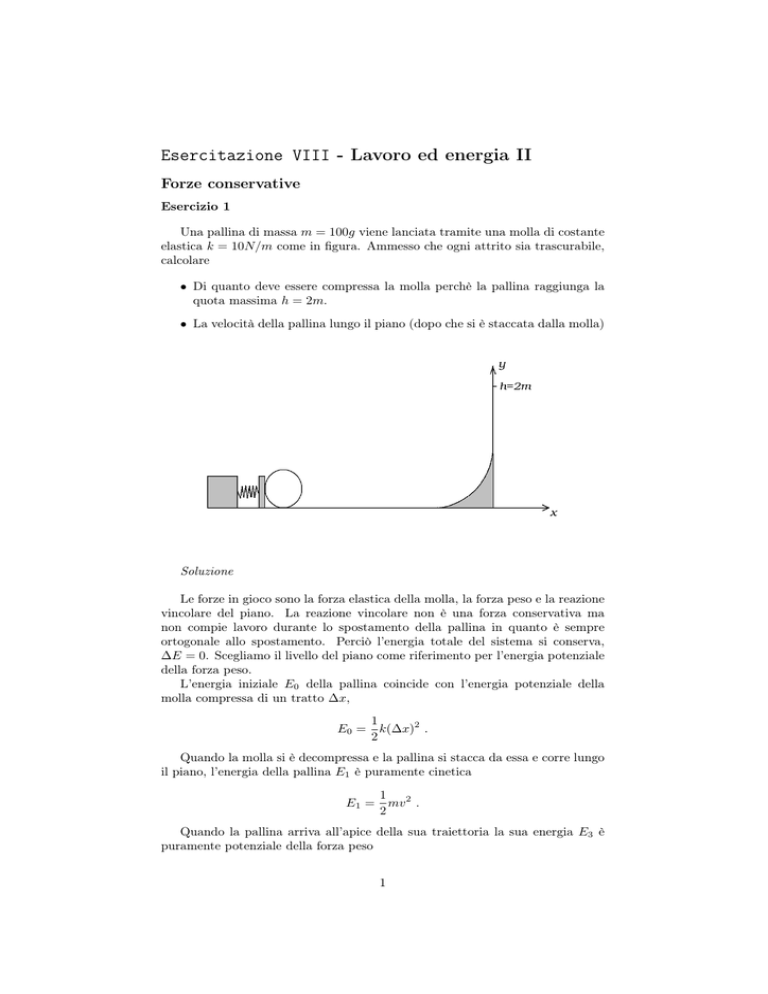
Esercizio 1
Una pallina di massa m = 100g viene lanciata tramite una molla di costante
elastica k = 10N/m come in figura. Ammesso che ogni attrito sia trascurabile,
calcolare
• Di quanto deve essere compressa la molla perchè la pallina raggiunga la
quota massima h = 2m.
• La velocità della pallina lungo il piano (dopo che si è staccata dalla molla)
Soluzione
Le forze in gioco sono la forza elastica della molla, la forza peso e la reazione
vincolare del piano. La reazione vincolare non è una forza conservativa ma
non compie lavoro durante lo spostamento della pallina in quanto è sempre
ortogonale allo spostamento. Perciò l’energia totale del sistema si conserva,
∆E = 0. Scegliamo il livello del piano come riferimento per l’energia potenziale
della forza peso.
L’energia iniziale E0 della pallina coincide con l’energia potenziale della
molla compressa di un tratto ∆x,
E0 =
1
k(∆x)2 .
2
Quando la molla si è decompressa e la pallina si stacca da essa e corre lungo
il piano, l’energia della pallina E1 è puramente cinetica
E1 =
1
mv 2 .
2
Quando la pallina arriva all’apice della sua traiettoria la sua energia E3 è
puramente potenziale della forza peso
1
E3 = mgh .
Poiché l’energia si conserva deve valere E0 = E1 = E3 .
Imponendo che E0 = E3 si ha
r
1
2mgh
2
k(∆x) = mgh ⇒ ∆x =
= 0.63m .
2
k
Si ricordi che la massa m va convertita in kg,
100g = 0.1kg .
Imponendo che E0 = E1 e sfruttando la conoscenza di ∆x si ha
r
1
1
k
2
2
k(∆x) = mv ⇒ v = ∆x
= 6.3m/s .
2
2
m
Forze non conservative
Esercizio 2
Una pallina di massa m = 0.2kg viene lanciata verticalmente verso il suolo
da un’altezza iniziale h0 = 1.4m e con una velocità iniziale il cui modulo è
v0 = 5m/s. Calcolare a quale altezza h1 arriva la pallina dopo aver rimbalzato
se nell’urto col suolo perde 2J.
Soluzione
L’energia iniziale della pallina è
E0 =
1
mv 2 + mgh0 = 5.244J .
2 0
L’energia finale della pallina, quando arriva all’apice della sua traiettoria
dopo aver rimbalzato, è
E1 = mgh1 .
A causa dell’urto col suolo l’energia della pallina non si conserva e la variazione dell’energia è ∆E = −2J (si osservi il segno meno)
v2
∆E
1
= 1.7m .
∆E = E1 − E0 = mgh1 − mv02 − mgh0 ⇒ h1 = h0 + 0 +
2
2g
mg
Si osservi che se l’energia si fosse conservata (urto elastico, ∆E = 0) si
avrebbe avuto
h1 = h0 +
v02
= 2.7m .
2g
Si osservi infine che se la pallina fosse stata fatta cadere da ferma (v0 = 0)
e l’urto fosse stato elastico si avrebbe avuto
h1 = h0 .
2
Esercizio 3
Un corpo di massa m = 4kg è sottoposto ad una forza costante di modulo
F = 35N la quale forma con l’orizzontale un angolo ϑ = 25◦ . Ammesso che
il corpo parta da fermo e che percorra inizialmente un tratto orizzontale liscio
di lunghezza l = 5m e poi un tratto orizzontale scabro di lunghezza s = 3m e
µ = 0.2, si calcoli la velocità finale del corpo.
Soluzione
La variazione di energia cinetica del corpo è data dal lavoro di tutte le forze
in gioco, ∆K = W . In quanto v0 = 0 si ha
r
2
vf =
W .
m
Nel tratto liscio le forze in gioco sono: la forza peso P~ , la reazione vincolare
~ e la forza F~ .
del piano N
Nel tratto scabro le forze in gioco sono: la forza peso P~ , la reazione vincolare
~ , la forza F~ e la forza d’attrito F~a . La forza d’attrito è una forza
del piano N
costante, diretta in maniera opposta al moto e di modulo
Fa = µ(mg − F sin ϑ) .
Dato che sia la forza peso che la reazione vincolare del piano non compiono
lavoro, il lavoro delle forze è
W = F (l + s) cos ϑ − µ(mg − F sin ϑ)s = 239J ,
da cui
r
vf =
2
[F (l + s) cos ϑ − µ(mg − F sin ϑ)s] = 10.9m/s .
m
Esercizio 4
Una pallina di massa m = 100g viene lanciata tramite una molla di costante
elastica k = 10N/m compressa di ∆x = 0.65m, come in figura. Per un tratto di
piano lungo s = 0.7m fra la pallina e il piano c’è attrito con µ = 0.2. Calcolare
• La velocità v1 con cui la pallina giunge nella zona in cui c’è attrito.
• La velocità v2 con cui la pallina esce dalla zona in cui c’è attrito.
• La quota massima h raggiunta dalla pallina.
Soluzione
L’energia si conserva nel tratto che va dalla molla alla zona in cui c’è attrito
(tratto 0-1) e nel tratto successivo alla zona in cui c’è attrito (tratto 2-3). Nella
zona in cui c’è attrito (tratto 1-2) l’energia non si conserva.
3
Introduciamo un sistema di coordinate come in figura. L’energia all’istante
iniziale in cui la molla è compressa è
E0 =
1
k(∆x)2 ,
2
in quanto la pallina è ferma, v0 = 0, e per il livello di riferimento scelto anche
y0 = 0.
Prima che la pallina entri nella zona in cui c’è attrito la sua energia è
E1 =
1
mv 2 .
2 1
Poiché l’energia si conserva nel tratto 0-1 la velocità v1 si trova imponendo
E0 = E1 ,
r
1
1
k
2
2
k(∆x) = mv1 ⇒ v1 = ∆x
= 6.5m/s .
2
2
m
Si ricordi di convertire la massa in kg! All’inizio del tratto in cui c’è attrito
l’energia cinetica della pallina è
K1 =
1
1
mv 2 = k(∆x)2 .
2 1
2
Al termine del tratto in cui c’è attrito l’energia cinetica della pallina è
K2 =
1
mv 2 .
2 2
La variazione di energia cinetica ∆K = K2 − K1 coincide con il lavoro di
tutte le forze in gioco nel tratto in cui c’è attrito. Dato che l’unica forza che
compie lavoro in questo tratto è la forza d’attrito, Fa = µmg, si ha
r
1
1
k
2
2
mv2 − k(∆x) = −µmgs ⇒ v2 =
(∆x)2 − 2µgs = 6.2m/s .
2
2
m
L’energia della pallina uscita dalla zona in cui c’è attrito è
E2 =
1
1
mv 2 = k(∆x)2 − µmgs .
2 2
2
4
Quando la pallina arriva alla quota massima y3 = h la sua energia è
E3 = mgh ,
in quanto all’apice della sua traiettoria la pallina è ferma. Nel tratto 2-3
l’energia si conserva, imponendo E2 = E3 si ha
1
k(∆x)2
k(∆x)2 − µmgs = mgh ⇒ h =
− µs = 2m .
2
2mg
Esercizio 5
Una pallina di massa m = 0.2kg viene lanciata da una molla di costante
elastica k1 = 15N/m compressa di ∆x1 = 0.1m. La pallina viaggia su un piano
orizzontale passando su di una zona lunga s = 0.05m con cui ha un attrito
µ = 0.3 e comprime infine una seconda molla con costante elastica k2 = 20N/m.
Calcolare di quanto si comprime la seconda molla.
Soluzione
Scegliamo come livello di riferimento del potenziale quello del piano su cui si
muove la pallina: in questo modo l’energia potenziale della forza peso della pallina è costantemente zero. L’energia iniziale della pallina coincide con l’energia
della prima molla compressa,
E0 =
1
k1 (∆x1 )2 = 0.075J .
2
L’energia finale della pallina coincide con l’energia della seconda molla compressa,
E1 =
1
k2 (∆x2 )2 .
2
A causa del passaggio sulla zona con attrito l’energia della pallina non si
conserva ma varia di una quantità pari al lavoro compiuto dalla forza d’attrito
lungo lo spostamento s,
∆E =
1
1
k2 (∆x2 )2 − k1 (∆x1 )2 = −Fa s = −µmgs = −0.0294J ,
2
2
da cui
r
∆x2 =
2µmgs
k1
(∆x1 )2 −
= 0.07m .
k2
k2
5
Si osservi che se si elimina la zona in cui c’è attrito (s = 0) si ottiene
r
k1
∆x2 = ∆x1
= 0.09m .
k2
Si osservi infine che in assenza di attrito e nell’ipotesi in cui le due molle
siano uguali (k1 = k2 ) si ottiene
∆x2 = ∆x1 .
6












