Luce colore visione

1
Introduzione alla fisica
La parola fisica deriva dalla parola greca ”physis” che significa natura. La
fisica è appunto la scienza che studia i fenomeni naturali, cercando di risalire
alle leggi che li governano e ai principi universali, da cui queste derivano. Il
fisico è colui che non si limita ad osservare i fenomeni naturali, ma è colui
che cerca di scoprire perchè essi si verificano. Di fronte ad un cielo blu, o ad
un grande arcobaleno, il fisico non si limita ad esclamare:”Che meraviglia”,
ma cerca di scoprire perchè il cielo è blu e perchè si è formato l’ arcobaleno.
La fisica si basa su un metodo scientifico, detto metodo sperimentale o
metodo scientifico.
Dalla parola stessa si puo’ comprendere che alla base di tale metodo stà la
sperimentazione.
Secondo tale metodo è necessario prima di tutto osservare il fenomeno, poi
formulate delle ipotesi sullo svolgimento dei fenomeni, confrontare queste
ipotesi con i risultati di opportune misure quantitative.
Come abbiamo visto in precedenza la fisica si occupa di studiare vari tipi di
fenomeni. In particolare l’acustica studia i fenomeni legati al suono, l’ottica
i fenomeni legati alla luce, al colore, alla visione, la meccanica il moto dei
corpi, la fisica nucleare le piccole particelle.
2
2.1
Luce colore e visione
Nascita della luce
”Fiat lux”: sia fatta la luce, cosı̀ disse il padreterno una volta creati cielo e
terra, prima di accingersi a formare il resto dell’universo. ”Et lux facta est”:
e la luce fu fatta. Dopo di che, constatato con qualche soddisfazione che la
luce non era niente male, egli la separò dalle tenebre. Poi, come ci hanno
raccontato, passò a creare il firmamento, le varie terre, i mari, le piante, gli
animali e le altre meraviglie del cosmo. La luce, dunque, secondo la leggenda, precedette ogni altra cosa, o quasi . D’altra parte, è lecito pensare che
anche il creatore onnipotente, se avesse dovuto lavorare al buio, si sarebbe
trovato in difficoltà, data la complessità immane della macchina che si era
prefisso di costruire. Quanto meno, avrebbe pestato la coda a una cometa
o finito per rovesciare la Via Lattea. Questa, naturalmente, è la leggenda.
Essa è stata motivo di fede per l’uomo attraverso i millenni, e fonte di ispirazione per grandi artisti. Nella realtà, sappiamo che esistono varie teorie
per spiegare l’origine del mondo, ma che di nessuna possiamo essere certi.
Se non altro, perché la presenza dell’uomo nella storia dell’universo risale a
tempi recentissimi. Siamo proprio gli ultimi venuti. Oggi, tra gli scienziati
trova il maggior credito la famosa teoria del big bang, o grande botto iniziale.
Una ventina di miliardi di anni fa, poco più poco meno, tutta la materia dell’universo sarebbe stata concentrata in un solo punto, costituendo un nucleo
1
Figura 1: La separazione delle tenebre dalla luce
primordiale di enorme densità: quello che si potrebbe definire una specie
di uovo cosmico. L’uovo cosmico sarebbe esploso scagliando frammenti di
materia tutto intorno a sé e da tali frammenti si sarebbero poi formate le
stelle e le galassie. È questa un’ipotesi confermata dal fatto che l’universo,
ancora oggi, appare in continua e rapida espansione, come mostrano, senza lasciare adito a dubbi, certi fenomeni osservati dagli astrofisici, come il
red shift da effetto Doppler. Ma per quanto solida e credibile, la teoria del
big bang va considerata pur sempre un’ipotesi, non bisogna dimenticarlo.
Perché, sebbene un po’ di fantasia e di immaginazione in molti casi servano
ad abbellire la vita, quando si viene a parlare di conoscenza, la nostra dignità di esseri raziocinanti ci impone di prendere per buono, in modo più
o meno definitivo, solo ciò che possiamo verificare in maniera concreta e
riproducibile. Ce lo ha insegnato per primo Galileo Galilei. E la nascita
dell’universo è sicuramente uno di quegli esperimenti scientifici che l’uomo
non sarà mai in grado di riprodurre e guardare da vicino!
Ma comunque siano andate le cose, mano del creatore, big bang o altre mirabili diavolerı́e, per quanto riguarda la comparsa della luce è difficile
avere dubbi sul fatto che essa si sia manifestata nell’istante stesso in cui è
esistita la materia, almeno quella che si presenta nelle forme a noi note. Non
sarebbe facile immaginare masse di materia in fase di evoluzione, corpi che si
trasformano, insomma processi fisici o chimici in atto, senza ammettere che
da essi venga sprigionata energia. Né sarebbe sensato aspettarsi che tale en2
ergia si accumuli indefinitamente sul corpo che l’ha generata, invece di essere
irradiata in qualche modo attraverso lo spazio circostante. Prendiamo ad
esempio un semplice caso, quello di ma comune lampadina a incandescenza.
A causa del passaggio della corrente elettrica, nel filamento viene dissipata
dell’energia. È il cosiddetto effetto joule, dal nome del fisico inglese che
Figura 2: Lampadina
intorno alla metà dell’Ottocento stabilı̀ i princı̀pi di trasformazione dell’energia da una forma in un’altra. Se l’energia prodotta restasse sul filamento,
la temperatura di quest’ultimo aumenterebbe rapidamente fino a farlo bruciare, il che avverrebbe nel giro di pochi istanti. Invece sappiamo che questo
non accade. Una volta girato l’interruttore, il filamento in un attimo si
scalda fino a raggiungere il cosiddetto calor bianco, ma a questo punto il
processo si arresta, perché l’energia generata fluisce di pari passo all’esterno
della lampadina. È appunto ciò che noi percepiamo come luce e calore. La
luce è dunque una forma di energia raggiante. Ma attenzione: quest’energı́a,
per uscire dalla lampadina, deve poter viaggiare anche attraverso il vuoto,
giacché il bulbo di vetro viene sempre evacuato per proteggere il filamento
dai fenomeni di ossidazione. Un discorso analogo vale per il Sole e per i
corpi celesti, salvo che i processi che portano alla produzione di energia sono
naturalmente di natura diversa dall’effetto Joule.
Come se ne va quest’energia dal corpo che l’ha generata? Sembra logico
pensare a qualche tipo di propagazione ondosa, come succede per il suono
che viaggia dalla sorgente all’ascoltatore tramite un moto, appunto di tipo
ondoso, delle particelle del mezzo ambiente (aria, acqua o materia solida).
Ma nel caso della luce si badi bene, c’è una fondamentale differenza: le onde
luminose, a differenza di quelle sonore, devono essere capaci di propagarsi
anche nel vuoto, sia esso quello della lampadina o quello dello spazio interstellare. Ebbene, onde di questo tipo in effetti esistono: sono quelle che ı́
fisici chiamano, per la precisione, onde elettromagneticbe.
Spiegheremo meglio nel seguito cos’è un’onda elettromagnetica. Per
adesso basterà dire che la luce cosiddetta visibile è appunto un particolare
3
tipo di onda elettromagnetica. Altre specie di onde elettromagnetiche sono
le onde radio, le microonde, il calore, i raggi X,e i raggi ultravioletti. La
luce si diversifica da queste per il fatto di essere percepita dall’occhio’umano.
Essa infatti è capace di stimolare, arrivando sulla retina, impulsi o segnali
nervosi che vengono trasmessi al cervello. Quest’ultimo li elabora e arriva
a ricostruire una perfetta e straordinaria immagine tridimensionale a colori
della realtà che ci circonda. Se vogliamo, una specie di telecamera realizzata dalla natura stessa, ma quanto più complessa e affascinante di quelle che
l’uomo del Duemila riesce a costruire con gli ultimi ritrovati dell’elettronica!
2.2
Fascino e significato della luce
E’ narurale che questa presenza costante della luce in tutto ciò che vive, si
evolve, si trasforma, finisca per legare ad essa l’idea di attività, di benessere,
di esistenza stessa. Non è un caso che nel corso della storia il Sole, la più
grande sorgente di luce naturale e di energia vitale che all’uomo è dato di
osservare da vicino, sia stato spesso adorato come un dio.
Oggi, nell’era dei computer e delle esplorazioni spaziali, del sole sappiamo vita, morte e miracoli. Sappiamo, per esempio, che esso è solo una
minuscola capocchia di fiammifero ı́ncandescente spersa tra quella miriade
di torce fiammeggianti che sono le stelle. Il senso di mistero che accompagna
gli oggetti del culto, è perduto, e il concetto del soprannaturale che l’uomo
porta con sé si è spostato verso divinità più astratte e meno verificabili.
Eppure non sono pochi quelli che al vecchio Sole amano attribuire ancora
miracolose doti curative dell’anima e del corpo. Chi di noi non prova la
sensazione di sentirsi in forma dopo aver preso una buona tintarella? Luce
è quindi anche sinonimo di felicità, sicurezza, fiducia. E naturalmente, per
ragioni ancora più ovvie, di chiarezza, di comprensione, di intelligenza. Pensate ai tradizionali modi di dire: ”la luce eterna”, ”far luce su un mistero”,
”ragionamento lucı́do”, ”mente illuminata”, ”personalità brillante”, ”volto
splendente”, ”sorriso luminoso”. E altri dello stesso genere. Cosı̀ come il
buio, l’oscurità, simbolizzano i concetti opposti: ”le tenebre dell’inferno”,
”oscurantismo del medioevo”; e ancora: ”avere un’aria cupa o un aspetto
tetro”, ”vedere tutto nero”, ”avere un carattere ombroso”, ”significato oscuro”. Solo Victor Hugo espresse un concetto che sfugge a questa automatica identificazione tra luce, chiarezza e vita. Disse: ”Vedo una luce nera”,
ma queste furono le sue ultime parole prima della morte. Un’eccezione, se
vogliamo’ che conferma la regola. Anche noi, forse, giunti al momento della
resa suprema, preferiremo aggrapparci all’idea bizzarra di una luce nera, di
una luce invisibile, piuttosto che ammettere che la vista, e con essa la vita,
ci sta sfuggendo.
La luce ci infonde un confortevole senso di sicurezza perché ci permette
di muoverci nell’ambiente senza timori o incertezze. Essa ci dà padronanza
delle cose, rivelandocde nelle loro forme, dimensioni e colori, consentendoci
4
di valutarne posizione, distanza e movimento. La luce, dunque, ci mette in
comunicazione col mondo esterno assai più direttamente di ogni altro veicolo
di informazione, quale il suono e le sensazioni tattili o olfattive. Essa è il
nostro strumento di indagine e di conoscenza più ricco e completo. Nulla
è più sconfortante, per usare ancora dei luoghi comuni, che muoversi alla
cieca o brancolare nel buio. Lo stesso padreterno, lo abbiamo visto nella
narrazione del Genesi, se ne era reso ben conto fin dal primo istante.
A parte gli usi naturali della luce, che hanno interessato gli uomini di
tutte le epoche, la tecnologia moderna ci permette cose straordinarie. Per
esempio di usare la luce, nella fattispecie fasci laser, per trasmettere dati,
telefonate o segnali televisivi a grandi distanze. E gli scienziati studiano e
comprendono a fondo le proprietà della materia analizzando in laboratorio
la sua capacità di trasmettere e riflettere la luce (o meglio le sue diverse
componenti cromatiche), ovvero di emetterla durante i processi di trasformazione fisica o chimica cui la materia stessa è sottoposta. È una tecnica,
questa, che si chiama spettroscopia e che può impiegare anche tipi di radiazione elettromagnetica non necessariamente visibili, come i raggi X o le
onde radio. È proprio con questa tecnica, esaminando le radiazioni che ci
giungono dallo spazio cosmico, che si sono tratti gli elementi utili a ipotizzare la teoria del big bang. E per restare sulla Terra, è con la spettroscopia
che si è capita l’intima costituzione degli atomi e delle molecole, o la meravigliosa architettura dei cristalli e dei complessi sistemi che costituiscono la
materia organica.
Facciamo un semplice ma significativo esempio. Ogni sostanza, bruciando, produce una fiamma che presenta colori caratteristici. Se una sostanza o
più sostanze sconosciute vengono immesse in una fiamma, basterà osservare
la luce emessa con strumenti capaci di distinguere i vari colori separatamente, per risalire alla natura e alla quantità delle sostanze presenti. Oggi
queste tecniche si mostrano di particolare interesse nello studio dell’inquinamento, poiché consentono di trovare anche piccole tracce di contaminanti e
di veleni presenti nell’aria, nell’acqua o nei terreni.
2.3
La visione umana
Se, da un lato, la scienza ha realizzato macchine e strumenti di grande perfezione, che nell’ultimo secolo hanno permesso di spiegare i più reconditi
segreti della natura attraverso l’esame della luce che la materia è capace
di emettere o di assorbire, dall’altro lato è vero che lo strumento ottico
più straordinario e complesso a disposizione dell’uomo è nato con lui: l’occhio, naturalmente, insı́eme a quella meravigliosa macchina che è il sistema
nervoso e che presiede alla elaborazione dei dati che provengono dal nervo
ottico. Con la visione dell’occhio umano, si entra in una sfera di percezioni
che sfuggono alla fredda e rigorosa obiettività dei dati di osservazione, per
coinvolgere sottili e spesso misteriosi comportamenti soggettivi ed esperien5
ze personali o ancestrali. Percezioni che portano al di là dei dati sensoriali,
dando all’immagine forme e significati più vari e articolati.
Figura 3: Un effetto dovuto alla nostra abitudine alla terza dimensione: le
3 ragazze sembrano di statura crescente da sinistra a destra
Figura 4: Un esempio di bistabilità della percezione visiva. Si contano 6 o 7
cubi a seconda che si imma gini di guardare la figura dall’alto verso il basso
o dal basso verso l’alto
6
2.4
Sorgenti di luce, corpi opachi e trasparenti
È a tutti noto che la vita sul nostro pianeta è possibile grazie alla presenza
del Sole, che illumina gli oggetti che noi vediamo. Il Sole è una sorgente
di luce. In generale, sono sorgenti di luce tuttı́ ı́ corpi che brillano di luce
propria. Sono sorgenti artificiali tutte le sostanze, riscaldate a una temperatura superiore agli 800 ◦ C. Il colore della luce emessa da queste sorgenti
dipende dalla temperatura: man mano che questa cresce si passa da un colore rossastro a un giallo brillante e infine al bianco. Anche il colore della
luce emessa da una lampadina a incandescenza varia con l’intensità della
corrente elettrica, passando, con l’aumentare di questa, gradatamente dal
rosso al bianco. Dall’esame del colore della luce emessa si può avere una
stima della temperatura della sorgente. Analizzando, per esempio, il colore
della luce emessa dalle stelle si ricava la loro temperatura; per il Sole è stata
ricavata una temperatura superficiale di 6000 ◦ C. Altre sorgenti artificiali di
luce sono le fiamme a gas, a petrolio, a olio ecc. che sfruttano la combustione di idrocarburi. Sorgenti invece che sfruttano la corrente elettrica sono,
oltre alle lampadine a incandescenza, i tubi a vapori di mercurio e al neon.
Questi ultimi però, a differenza delle sorgenti a combustione, emettono luce
di colore caratteristico a seconda del gas contenuto nel tubo; al variare dell’intensità di corrente che attraversa il gas, varia la luminosità della sorgente,
ma non il colore, che invece rimane inalterato. I tubi al neon inoltre, a differenza delle lampadine a incandescenza, rimangono freddi, anche quando
emettono luce; in queste sorgenti si utilizza l’eccitazione del gas prodotta
dalla corrente elettrica. I gas, una volta eccitati, ritornano nelle condizioni
primitive emettendo sotto forma di luce l’energia assorbita nell’eccitazione.
La maggior parte degli oggetti visibili sono però corpi ı́lluminati che ricevono
la luce da qualche sorgente e la diffondono in tutte le direzioni; la Luna, per
esempio, è visibile perché diffonde la luce del Sole. La percentuale di luce
diffusa dipende dal colore dei corpi; quelli scuri assorbono la maggior parte
della luce, mentre in quelli chiari prevale la quantità di energia luminosa
diffusa. È a tutti noto che la luminosità di una stanza, a parità di altre
condizioni, è tanto maggiore quanto più chiare sono le pareti. Alcuni corpi, come lastre di vetro, l’aria, l’acqua, si lasciano attraversare dalla luce
permettendo di vedere gli oggetti che si trovano dalla parte opposta dell’osservatore; questi corpi sono chiamati trasparenti. La trasparenza di un
corpo dipende però, oltre che dalla sua natura, dallo spessore; l’acqua del
mare è trasparente per piccole profondità, mentre a 500 m di profondità c’è
il buio assoluto. Analogamente i metalli, che in condizioni normali non si
lasciano attraversare dalla luce, diventano trasparenti se hanno un piccolo
spessore; è trasparente, per esempio, una sottile lamina d’oro.
Tutti quei corpi, come i metalli, il legno ecc. che non si lasciano attraversare dalla luce sono detti opachi. Oltre ai corpi trasparenti e a quelli opachi,
vi sono poi i cosiddetti corpi traslucı́dı́ i quali fanno passare la luce,ma non
7
permettono di distinguere gli oggetti: ne sono esempi il vetro smerigliato, il
vetro bianco, la carta ecc.
2.5
Propagazione della luce
La luce, anche se attraversa un mezzo trasparente, non ha bisogno di questo
come sostegno per la sua propagazione: la luce del Sole infatti giunge a
noi attraversando lo spazio vuoto. La prima proprietà della luce facilmente
evidenziabile riguarda la sua propagazione rettilinea. Se, per esempio, osserviamo un sottile fascio di luce che da una piccola fessura penetra in una
stanza tenuta al buio attraversando il pulviscolo disperso nell’aria, notiamo
in modo evidente il percorso rettilineo della luce che, in modo convenzionale,
identifichiamo con i raggi luminosi. Diciamo subito che il concetto di raggio
luminoso, rappresentato da una linea retta, non corrisponde a una realtà
concreta: si tratta solo di uno schema utile, praticamente di un modello per
studiare una serie di fenomeni compresi nella cosiddetta ottica geometrica
chiamata anche ottica dei raggi. La propagazione rettilinea della luce in un
mezzo è indirettamente confermata dalla formazione delle ombre.
Un corpo opaco M, disposto fra una sorgente luminosa puntiforme e uno
schermo, origina su questo una zona d’ombra corrispondente ”solo” ai raggi
intercettati dal corpo, senza cioè che esista un processo di aggiramento come
potrebbe avvenire se la luce non si propagasse in linea retta.
Se la sorgente luminosa è piuttosto estesa, sullo schermo appare , oltre
alla zona d’ombra dove non arrivano i raggi emessi dalla sorgente, anche una
zona di penombra dove arriva solo la luce proveniente dai bordi della sorgente. Un’altra conferma della propagazione rettilinea deriva dai fenomeni
connessi con le eclissi di Sole o di Luna. Nel primo caso, quando la Luna si
trova allineata fra il Sole e la Terra, la zona della Terra che viene a trovarsi
nel cono d’ombra proiettato dalla Luna è in completa oscurità (eclissi totale), mentre la zona che viene a trovarsi nel cono della penombra vede solo
uno spicchio del Sole (eclissi parziale). Nell’eclissi di luna il nostro satellite
appare scuro in quanto viene a trovarsinell’ombra proiettata dalla terra.
8
2.6
Riflessione della luce
Consideriamo un raggio luminoso che incontra la superficie di separazione di due mezzi trasparenti diversi che abbiamo contrassegnato con
i numeri 1 e 2. L’esperienza mette in evidenza che il raggio incidente dà
luogo a due raggi, di cui uno, chiamato raggio riflesso, ritorna nel primo
mezzo, mentre l’altro, chiamato raggio rifratto, penetra nel secondo mezzo,
ove però si propaga in una direzione diversa da quella del raggio incidente.
Siamo in presenza di due fenomeni, la riflessione e la rifrazione della luce.
Evidentemente, l’energia luminosa in parte si riflette e in parte si rifrange.
Ci occupiamo dapprima della riflessione della luce e delle sue applicazioni
e successivamente della rifrazione e delle applicazioni connesse con questo
fenomeno.
Osserviamo però fin d’ora che nel secondo mezzo si ha un solo raggio
rifratto se il raggio di luce incidente è di un ben determinato colore, cioè se
è un raggio monocromatico. Se invece nel raggio incidente ci sono radiazioni
di vario colore, se cioè esso è un raggio di luce composta, come può essere un
raggio solare, nel secondo mezzo si hanno tanti raggi diversamente colorati,
quanti sono i colori presenti nel raggio incidente. Ma questo lo vedremo più
avanti. Ritornando alla riflessione, chiamiamo angolo di incidenza i quello
9
formato dal raggio incidente con la normale alla superficie riflettente nel
punto di incidenza, e angolo di riflessione i quello formato dal raggio riflesso
con la stessa normale.
La riflessione avviene rispettando le seguenti due leggi sperimentali:
1. il raggio incidente, la normale alla superficie riflettente nel punto di
incidenza e il raggio riflesso giacciono nello stesso piano.
2. l’angolo di incidenza i è uguale all’angolo di riflessione i’.
Sono due leggi che possono essere facilmente verificate sperimentalmente,
per esempio a mezzo dell’apparecchiatura riportata in figura. Il dispositivo
è formato da un disco che permette la lettura degli angoli sia di incidenza che
di riflessione. Al centro del disco e parallelamente a un diametro è disposto
uno specchio piano che riflette un pennello luminoso proveniente da una
sorgente. Si vede chiaramente che il raggio riflesso si trova nello stesso piano
del raggio incidente e della normale alla superficie riflettente e che l’angolo
di riflessione e quello di incidenza sono uguali tra loro. Il disco inoltre può
ruotare intorno a un asse orizzontale, per cui è possibile verificare le leggi
della riflessione con vari angoli di incidenza. Ottime superfici riflettenti
sono quelle metalliche, le quali, se ben levigate, costituiscono delle superfici
speculari piane o curve. Se invece la superficie riflettente è scabra, avviene
il fenomeno della diffusione. A tal fine è da osservare che certe superfici,
che a prima vista sembrano lisce, presentano molto spesso, sia pure a livello
microscopico, una struttura scabra.
10
2.7
Specchi piani
Consideriamo una superficie speculare piana dotata di forte potere riflettente, comunemente chiamata specchio piano. Sia inoltre P una sorgente
puntiforme. Applicando le leggi della riflessione, costruiamo i raggi riflessi
provenienti dai raggi incidenti PI, PI’ ecc. I raggi riflessi divergono, mentre i loro prolungamenti geometrici si incontrano nel punto P’, simmetrico
di P rispetto allo specchio. Infatti se P’ è l’intersezione del prolungamento del raggio riflesso per I con la normale da P allo specchio. Infatti se
P’è l’intersezione del proloungamento del raggio riflesso pe I con la normale
da P allo specchio, dall’uguaglianza degli angoli d’incidenza e di riflessione
segue l’uguaglianza dei triangoli rettangoli PHI e P’HI. Risulta perciò PH
= P’H. Poiché il ragionamento può essere ripetuto per qualsiasi raggio riflesso, concludiamo che i prolungamenti dei raggi riflessi s’intersecano nel
punto P’simmetrico di P rispetto allo specchio. Una persona posta davanti
allo specchio, ricevendo i raggi riflessi, ha l’illusione che questi provengano
tutti da P’. Diciamo per questo che P’ è l’immagine virtuale di P, virtuale o
fittizia perché per un osservatore i raggi si comportano come se provenissero
da P’ e non da P . L’immagine di un oggetto di dimensioni finite si può
ottenere ripetendo lo per ogni punto la costruzione appena esposta: il luogo
dei punti immagine rappresenta l’immagine dell’oggetto.
Come si può verificare, l’immagine in generale non è uguale all’oggetto; sebbene presenti sempre le medesime dimensioni dell’oggetto, lo risulta
sovrapponibile a esso. Per questo motivo, se davanti a uno specchio piano
poniamo un foglio di un libro, i caratteri appaiono rovesciati; se si alza la
mano destra, l’immagine alza la sinistra .
2.8
Specchi sferici
Applichiamo ora le leggi della riflessione agli specchi sferici, che sono calotte
sferiche dotate di notevole potere riflettente. Gli specchi sferici si dividono
in:
11
1. specchi concavi, se la superficie speculare è quella interna della
calotta.
2. specchi convessi se la superficie speculare è quella esterna.
2.9
Elementi caratteristici
Gli elementi caratteristici per lo studio della riflessione su uno specchio
sferico sono:
1. centro di curvatura: centro C della superficie sferica alla quale appartiene la calotta;
2. asse ottico principale: rappresenta l’asse di simmetria della superficie
speculare passante per C;
3. vertice: punto V di intersezione dell’asse ottico principale con la calotta sferica;
4. angolo di apèrtura: angolo ACB compreso fra i due raggi condotti dal
centro con gli estremi dell’arco sezione AVB.
Anche se tutte le proprietà degli specchi sferici possono essere dedotte
facendo riferimento a uno specchio qualsiasi lo studio viene di solito condotto
facendo riferimento agli specchi compresi entro le cosiddette approssimazioni
di Gauss espresse dalle seguenti condizioni:
1. piccolo angolo di apertura, in modo che la porzione di calotta sferica sia
molto piccola rispetto alla superficie sferica alla quale essa appartiene;
12
2. raggi parassiali, nel senso che i raggi luminosi che giungono sullo specchio sono poco inclinati rispetto all’asse ottico principale e quindi
formano con esso angoli molto piccoli.
2.10
Fuochi
Ciò premesso, consideriamo un fascio di raggi paralleli all’asse che incontrano
uno specchio concavo. Tenuto conto che la normale alla superficie riflettente
in un punto, perpendicolare al piano tangente per quel punto, corrisponde
al raggio della superficie sferica alla quale appartiene la calotta, costruiamo,
mediante le leggi della riflessione, il raggio riflesso corrispondente a ogni
raggio incidente. Sia graficamente che sperimentalmente si constata che se
sono soddisfatte le approssimazioni di Gauss, i raggi riflessi convergono in
un punto F, giacente sull’asse e chiamato fuoco principale dello specchio.
Come vedremo più avanti , il fuoco si trova con notevole approssimazione
nel punto medio di VC cosicché la misura del segmento VF, chiamata distanza focale e comunemente indicata con f, è pari alla metà del raggio R
di curvatura dello specchio. Nel caso degli specchi convessi, la costruzione
geometrica mostra, e l’esperienza conferma, che un fascio di raggi paralleli
all’asse principale, dopo la riflessione, diverge come se provenisse dal punto
medio F del raggio VC. In analogia con gli specchi concavi, tale punto è
chiamato fuoco principale: esso è però virtuale, cioè fittizio, in quanto il
luogo di incontro dei prolungamenti dei raggi riflessi non rappresenta, nel
caso in esame, alcuna concentrazione d’energia luminosa associata ai raggi riflessi. Per ragioni di opportunità grafiche, nel disegnare gli specchi,
queste condizioni sono generalmente alterate. Inoltre, in luogo di raffigurare la calotta sferica, gli specchi sono rappresentati mediante un arco di
circonferenza ottenuto sezionando la calotta sferica con un piano passante
per l’asse principale.
13
2.11
La costruzione grafica dell’immagine negli specchi sferici concavi
Tra tutti i possibili raggi luminosi, che da un punto-oggetto vanno verso
uno specchio concavo, tre sono quelli particolarmente utili per localizzare il
corrispondente punto-immagine.
1. Un raggio parallelo all’asse principale il cui raggio riflesso passa per il
fuoco.
2. Un raggio che passa per il fuoco e che viene riflesso parallelamente
all’asse principale.
3. Un raggio che passa per il centro di curvatura e che viene riflesso di
nuovo per il centro di curvatura.
1. Se l’oggetto si trova tra il fuoco e il centro, l’immagine dell’oggetto è reale capovolta e ingrandita.
Inoltre, dal momento che i raggi convergono realmente nel punto
I e passano attraverso di esso, su un foglio di carta posto in I apparirà un’immagine luminosa della lampadina. Si tratta di un’immagine reale: se un immagine è reale, la luce passa realmente attraverso
di essa, riproducendo l’ oggetto.
14
2. Se l’oggetto si trova tra il fuoco e lo specchio, l’immagine è
virtuale, diritta e ingrandita
Come potete notare dalla figura i raggi divergono ed è come se provenis-
sero tutti da un punto al di là dello specchio. Quella che si forma è
quindi un’immagine virtuale.
3. Se l’oggetto si trova al di là del centro dello specchio, l’immagine è reale, capovolta e ridotta
15
2.12
La costruzione grafica dell’immagine negli specchi sferici convessi
Tra tutti i possibili raggi luminosi, che da un punto-oggetto vanno verso
uno specchio concavo, tre sono quelli particolarmente utili per localizzare il
corrispondente punto-immagine.
1. Un raggio parallelo all’asse principale il cui raggio viene riflesso come
se provenisse dal fuoco.
2. Un raggio diretto verso il punto focale che viene riflesso parallelamente
all’asse principale.
3. Un raggio diretto verso il centro di curvatura e che viene riflesso su se
stesso.
Dal disegno si puo’ notare che l’immagine appare virtuale, diritta e rimpicciolita.
2.13
Formula dei punti coniugati negli specchi
Si puo’ dimostrare che, entro le approssimazioni di Gauss, vale per specchi
concavi e convessi la seguente relazione:
1
1 1
+ =
p q
f
dove p è la distanza di un oggetto dallo specchio e q la distanza dell’ immagine di p dallo specchio e f la distanza focale. La formula permette di
calcolare la posizione dell’immagine di un oggetto, una volta nota la distanza
focale e la distanza dell’oggetto dallo specchio. Bisogna però tener presente
che:
1. la distanza dell’immagine è positiva se l’immagine è situata davanti
allo specchio (immagine reale) e negativa se l’immagine si trova dietro
di esso (immagine virtuale)
2. la distanza focale è positiva per uno specchio concavo negativa per uno
convesso.
16
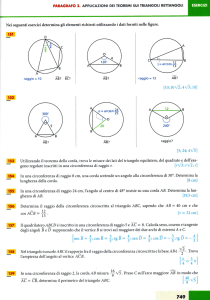
Esercizi
1. Uno specchio concavo ha raggio di curvatura r = 20cm; determinare
la posizione dell’immagine di un oggetto posto successivamente a 15
cm , a 5 cm e a 40 cm dal vertice.
2. Uno specchio con un raggio di curvatura di 100 cm viene utilizzato per
riflettere la luce proveniente da un oggetto posto a 75 cm di fronte ad
esso. Trovare la posizione dell’immagine.
2.14
Rifrazione
Con il termine rifrazione s’intende quel fenomeno nel quale un raggio luminoso, attraversando la superficie di separazione di fra 2 mezzi materiali, detti
primo mezzo e secondo mezzo, modifica la propria direzione di propagazione.
La rifrazione puo’ essere facilmente verificata utilizzando il dispositivo
in figura dove si osserva la rifrazione aria-vetro. Si puo’notare che ad un
angolo d’incidenza di 50 gradi corrisponde un angolo di rifrazione di 30
gradi. Si puo’ però anche notare che, se il raggio incidente coincide con la
normale alla superficie, il raggio rifratto è la propagazione rettilinea di quello
incidente. Possiamo inoltre osservare che se un raggio luminoso si propaga da
un mezzo meno denso(aria-vuoto) ad uno più denso( vetro-acqua) il raggio
rifratto si avvicina alla normale alla superficie e viceversa, se un raggio
luminoso si propaga da un mezzo più denso(vetro-acqua) ad uno meno denso
(aria-vuoto) il raggio rifratto si allontana dalla normale alla superficie.
2.15
Riflessione totale
Se un raggio luminoso si propaga da un mezzo più denso ad un mezzo meno
denso si puo’ verificare il fenomeno della riflessione totale. Consideriamo
2 mezzi uno più denso(acqua) ed uno meno denso(aria) e poniamo una
sorgente luminosa S nel mezzo più denso.
17
Poichè i raggi che si rifrangono da un mezzo più denso ad un mezzo meno
denso si allontanano dalla normale, considerando successivamente raggi incidenti provenienti da S e formanti con le rispettive normali angoli d’incidenza
via via crescenti, si perviene ad un raggio con un angolo d’incidenza l tale
che il raggio rifratto emerge radente la superficie di separazione dei 2 mezzi.
E’ chiaro che in queste condizioni l’angolo di rifrazione è di 90◦ . L’angolo l
viene detto angolo limite.
2.16
Fenomeni legati alla rifrazione
La rifrazione della luce è causa di una grande varietà di fenomeni ”apparenti” che si presentano molto spesso alla nostra visione. Oltre al banale
remo immerso nell’acqua che appare spezzato, a tutti è familiare il tremolio
delle sagome delle persone e degli oggetti su strade o spiagge arroventate
dal Sole, il luccichio delle stelle, o la deformazione ovale del Sole quando
è prossimo all’orizzonte. E chi non conosce i miraggi, da quello frequentissimo delle inesistenti macchie di bagnato sull’asfalto nei giorni di calura,
macchie che sembrano correre via dinanzi a noi quando avanziamo verso
di esse a quelli meno comuni della visione ingannevole di monti sorgenti
dalle acque o di evanescenti città collocate all’orı́zzonte (effetto ”Fata Morgana”)? Ognuno di questi fenomeni risale al meccanismo della rifrazione
della luce, cioè alla deviazione dal normale percorso rettilineo dei raggi luminosi quando attraversano un mezzo di densità non uniforme, dove la velocità di propagazione, come conseguenza, non si mantiene costante. In un
mezzo meno denso, infatti, la velocità della luce è più grande che in uno più
denso: l’apparente spezzamento di un remo nel passaggio dall’aria all’acqua
è dovuto appunto alla diversa inclinazione che prendono i raggi luminosi andando dalla prima, dove hanno una velocità di 300.000 km/s, alla seconda,
dove hanno una velocità di circa 225.000 km/s. L’effetto ”remo spezzato”
può essere ricreato in casa immergendo un fiore in un bicchiere. Il gambo di
un fiore immerso in un d’acqua, come illustra la fotografia.
18
2.16.1
Parallelo meccanico della rifrazione
Vediamo di capire, con un semplice esperimento meccanico, perché una variazione di velocità da un mezzo all’altro comporta una variazione di direzione
di avanzamento. Supponiamo di avere un piano perfettamente levigato con
al centro una zona invece molto ruvida, tale da rallentare la velocità di un
oggetto che si trovi a rotolare su di essa. Si può eseguire questo piccolo
esperimento usando un piano costituito da due fogli di cartone liscio e uno
di carta vetrata, occorre che i bordi combacino perfettamente, senza scalini
e lanciando sopra di esso due rotelline collegate solidalmente a un mozzo.
Si osservi bene la figura, dove la direzione del moto è scelta in modo che
l’asse delle rotelline non sia parallelo al confine tra i due mezzi e quindi la
rotellina A vi giunga prima della B. Sul mezzo ruvido, A riduce la sua velocità, mentre B prosegue alla velocità iniziale fino al momento in cui anch’essa
tocca il confine. Come conseguenza, il mozzo ruota e la sua direzione di
avanzamento, dopo il confine, risulta più inclinata rispetto al confine stesso. All’uscita dalla zona ruvida, il ragionamento si capovolge e il carrello
riacquista la primaria direzione di moto. Analogo è il comportamento di un
raggio di luce nel passaggio da un mezzo meno denso, come l’aria, a uno più
denso, come l’acqua, dove la sua velocità scende: il raggio si avvicina alla
normale alla superficie di separazione tra i due mezzi. La celeberrima legge
che descrive tale deviazione del raggio è nota come legge dei seni, o anche
legge di Cartesio presso di noi e legge di Snell nei paesi anglosassoni. Poiché
19
l’indice di rifrazione (n) è il rapporto tra la velocità della luce nel vuoto (c)
e quella nel mezzo materiale(v) , si dice che l’acqua ha un più alto indice di
rifrazione che l’aria.
c
n=
v
Va notato che l’indice di rifrazione di un mezzo è diverso per 1e diverse
componenti cromatiche che costituiscono la luce bianca, quindi l’angolo di
rifrazione è differente per ciascuna di esse. Come conseguenza, ogni componente, subendo una propria deviazione, si scinde dalle altre (fenomeno della
dispersione della luce). Nel caso dei mezzi trasparenti più comuni acqua,
vetro e quarzo l’indice di rifrazione cresce andando dal rosso al violetto,
quindi il primo devia meno del secondo, e le altre componenti cromatiche
vengono disperse su angoli compresi tra i due valori estremi.
2.16.2
Bastone spezzato e monetina rialzata
Iniziamo con la descrizione di un esperimento noto anche agli antichi greci
e originato dalla deviazione prodotta dalla rifrazione dei raggi luminosi. In
figura una moneta si trova sul fondo di un recipiente pieno di acqua. Il
raggio luminoso disegnato in figura con origine nel punto P della moneta,
rifrangendosi nel punto I della superficie libera dell’acqua, cambia direzione.
Per l’osservatore che riceve il raggio rifratto è come se il raggio avesse viaggiato sempre nella stessa direzione. Egli perciò vede l’immagine del punto P
nel punto P’. più vicino alla superficie libera dell’acqua; ne segue che tutta
la moneta sembra innalzarsi. Lo stesso effetto si verifica con un bastone
parzialmente immerso in acqua, cioè ogni punto del bastone immerso nell’acqua appare più vicino di quanto realmente è alla superficie attraverso
la quale viene osservato. Pertanto un bastone, parzialmente immerso in un
recipiente pieno di acqua con pareti trasparenti, come quelle di un bicchiere
di vetro, appare piegato a un osservatore che lo vede attraverso la superficie
libera dell’acqua e spezzato a un osservatore che lo vede attraverso la superficie di separazione dell’acqua dalla parete trasparente. Un osservatore
disposto in modo da poter vedere il bastone immerso attraverso entrambe
le superfici vede contemporaneamente la parte piegata e la parte spezzata.
20
2.16.3
Miraggio e fata Morgana
Generalmente gli strati dell’aria atmosferica più vicini alla terra sono anche
quelli più densi e gli strati superiori sono invece meno densi. Se però la terra
è molto calda può accadere che gli strati più bassi, che sono a più diretto
contatto col suolo, siano meno densi degli strati superiori. Questo avviene
nelle giornate molto calde d’estate e più frequentemente nei deserti.
Consideriamo allora un raggio luminoso che parte dalla cima S di un albero propagandosi verso suolo. Esso nel suo percorso incontra strati d’aria
sempre meno rifrangenti e quindi si rifrange allontanando; dalla normale
e diventando sempre meno obliquo. Siccome la rifrazione avviene sempre
da uno strato più rinfrangente a uno strato meno rifrangente, l’angolo di
incidenza cresce sempre di più, e a un certo momento supererà il valore
dell’angolo limite. In tali condizioni, per quanto già sappiamo, avviene il
fenomeno della riflessione totale e di conseguenza il raggio si allontana dal
suolo. Se il raggio riflesso totalmente incontra l’occhio di un osservatore, per
l’osservatore è come se avesse avuto sempre la stessa direzione, cioè come se
fosse pai tito da S’ e non da S. Di conseguenza l’osservatore vede in S’ l’immagine di S, proprio come se l’albero si fosse riflesso in uno specchio d’acqua.
In ciò consiste il fenomeno del miraggio, nel fatto cioè che l’osservatore vede
insieme l’oggetto e l’immagine. Viceversa, se gli strati d’aria più alti sono
molto meno densi di quelli più bassi, un raggio luminoso che va verso l’alto
segue un percorso curvilineo allontanandosi sempre più dalla normale. A un
certo punto avviene la riflessione totale e il raggio ritorna nuovamente verso
il basso. E’ questo il fenomeno di fata Morgana, della strega che aveva il
potere magico di creare castelli in aria ai tempi di re Artù.
21
2.16.4
Specchio d’asfalto
Siamo ora in grado di spiegare come nasce il miraggio delle chiazze di
bagnato sull’asfalto rovente. Prendiamo i raggi di luce che dal cielo arrivano
all’asfalto con un modesta inclinazione (raggio 1 della figura ). Se l’asfalto
scotta, l’aria prossima a esso è molto calda e si raffredda man mano che si sale
in altezza. L’aria calda è meno densa di quella fredda, dunque il suo indice
di rifrazione è minimo a livello del suolo e cresce gradualmente con la quota.
Ciò determina una continua deflessione del raggio verso l’alto man mano che
questo si avvicina al suolo e, se l’an- golo di incidenza è opportuno, il raggio
non arriva mai a toccare l’ asfalto, risalendo invece come per una apparente
riflessione. La sensazione di chi lo riceve è che l’asfalto sia ”bagnato” e si
comporti come uno specchio. Ciò avviene per angoli attorno a un preciso
valore, come mostra la figura, dove soltanto il raggio 1 è deflesso in modo
da colpire l’occhio dell’osservatore, mentre il raggio 2 sfila via sotto di esso
e i raggi 3 e 4 vanno a incidere sull’asfalto. Per tale motivo, se l’osservatore
avanza, anche la chiazza ”bagnata” deve avanzare, mantenendo sempre la
stessa distanza da lui. Questo tipo di miraggio è detto miraggio inferiore,
perché l’oggetto appare al di sotto della sua reale posizione.
2.16.5
Isole apparentemente vicine
Anche il mare può offrire visioni del tipo ”Fata Morgana”. La più nota e
frequente è la comparsa di fronte alle navi di isole montagnose che invece sono
assai lontane, addirittura sotto la linea dell’orizzonte. Il fenomeno ha fatto
gridare ”terra, terra!” a tanti marinai stremati da una lunga navigazione.
Non si tratta però di allucinazioni ma di visioni reali. Il fenomeno è dovuto
all’esatto contrario del miraggio dell’asfalto bagnato. Se l’acqua è più fredda
dell’aria, si crea un gradiente di temperatura dal basso verso l’alto, quindi la
densità dell’aria scende con la quota; ciò induce un incurvamento dei raggi
luminosi all’ingiù, vale a dire che essi seguono la curvatura della Terra. La
vedetta sulla nave vede l’isola ben prima che essa emerga fisicamente sopra
l’orizzonte, ma l’abitudine a situare gli oggetti sul diretto prolungamento
del raggio luminoso che perviene all’occhio lo spinge a giudicare che l’isola
22
si trovi sopra all’orizzonte. Questo meccanismo fa si che si possa vedere il
disco solare per qualche tempo dopo che esso è veramente tramontato.
2.16.6
Fibre ottiche
La fibra ottica è costituita da un nucleo centrale trasparente circondato una
parete meno densa rispetto al nucleo. La luce, incidendo in modo quasi
radente la parete interna del filo, viene interamente rı̀flessa e si propaga da
un estremo all’altro senza apprezzabili perdite. (Ricordo che il fenomeno
della riflessione totale si ha quando l’angolo d’incidenza è maggiore dell’angolo limite). In medicina e chirurgia le fibre ottiche, in pratica una treccia di
fili, permettono di esplorare con un pennello di luce parti interne del corpo
umano, siano esse organi o vasi sanguigni. In telefonia, esse vengono usate
per trasportare un grandissimo numero di segnali, assai più che i tradizionali
cavi di rame, dalla stazione trasmittente alla ricevente. Per questo occorre,
naturalmente, una conversione da segnale elettrico a impulso ottico e viceversa, cosa che oggi è resa possibile dai microscopici laser e convertitori a
semiconduttore.
2.16.7
Il mare come uno specchio
Perché qualsiasi superficie capace di riflettere, se osservata con luce quasi
radente, appare riflettente al 100% come uno specchio perfetto, come per
23
esempio i riflessi in un lago del sole e della luna quando sono bassi sull’orizzonte?
Il potere riflettente di una superficie che separa due mezzi diversi varia
con l’angolo di incidenza della luce. Per riferirsi al caso specifico aria-acqua,
la luce che incide circa perpendicolarmente sull’acqua viene riflessa in misura
del 2%. La riflessione rimane circa costante per angoli di incidenza obliqua
non troppo grandi, ma cresce rapidamente quando la luce incide con angoli
superiori ai 60 per raggiungere il 100% a incidenza radente. In questo limite, l’acqua appare un autentı̀co specchio e il suo colore diventa del tutto
impercepibile, persino nel caso in cui fosse intensamente colorata. Lo stesso
vale, naturalmente, per altre coppie di mezzi, per esempio aria-vetro.
2.16.8
Moltiplicazione dei pesci
Nel caso in esame, esistono sempre due vie perfettamente equivalenti,
per u n raggio luminoso che parte dal pesce ed arriva all’occhio della persona: una a destra e l’altra a sinistra dello spigolo. Poiché siamo abituati
a collocare gli oggetti che vediamo sulla linea retta uscente dall’occhio, si
otterranno due immagini ben separate e distinte del pesce.
24
2.17
Le lenti
Esse costituiscono la base fondamentale di conoscenza per la costruzione
degli strumenti ottici. In questi dispositivi (lenti per occhiali, microscopi,
cannocchiali, macchine fotografiche ...) la luce viene guidata lungo un percorso prestabilito e ben determinato. Parti essenziali degli strumenti ottici
sono le lenti sferiche, cioè corpi trasparenti limitati da 1 o 2 superfici sferiche.
Esse hanno la proprietà di produrre, senza sensibili deformazioni, immagi-
ni ingrandite o rimpicciolite degli oggetti.Un raggio di luce che colpisce la
superficie di una lente subisce due volte il fenomeno della rifrazione: una
prima volta nel passare dall’aria al vetro e una seconda nel passare dal vetro
all’aria. Nel seguito considereremo le lenti sottili. Esse hanno la proprietà
di avere uno spessore piccolo rispetto ai raggi delle superfici sferiche che le
delimitano. Una delle due superfici può anche avere raggio infinito, cioè essere un piano. Esistono perciò lenti di forme molto diverse ma, dal punto di
vista dell’effetto che producono, esse possono essere classificate in due soli
gruppi:
1. Lenti convergenti: sono più spesse al centro che ai bordi. Si chiamano cosı̀ perché fanno convergere in un punto sull’asse ottico,detto
fuoco, un fascio di raggi paralleli che le colpisce. L’esperienza mostra
che per una lente sottile i due fuochi si trovano sempre alla stessa
25
distanza rispetto al suo centro. I raggi del Sole, che arrivano sulla Terra praticamente paralleli, possono essere concentrati nel fuoco di una
lente convergente, dove riescono a incendiare un pezzo di carta. Sono
convergenti le lenti di ingrandimento, quelle degli occhiali da presbite
e da ipermetrope.
2. Lenti divergenti: sono più spesse ai bordi che al centro. Quando
sono colpite da un fascio di raggi paralleli lo fanno divergere. Le lenti
per gli occhiali da miope e quelle per lo spioncino della porta di ingresso
sono divergenti.
2.17.1
Formazione delle immagini in una lente convergente
Per la trovare graficamente l’immagine di un oggetto AB illuminato posto
davanti ad una lente convergente utilizziamo 2 raggi particolari.
1. Un raggio parallelo all’asse ottico che converge nel fuoco.
2. Un raggio che passa per il centro della lente e che non viene praticamente deviato. (il centro della lente si comporta come una lastra
a faccie piane e parallele. I raggi subisono 2 leggere deviazioni senza
però cambiare direzione)
Rappresentiamo le lenti convergenti con l:
26
2.17.2
Formazione delle immagini in una lente divergente
Per la trovare graficamente l’immagine di un oggetto AB illuminato posto
davanti ad una lente divergente utilizziamo 2 raggi particolari.
1. Un raggio parallelo all’asse ottico che diverge e i cui prolungamenti
s’incontrano nel fuoco virtuale.
2. Un raggio che passa per il centro della lente e che non viene praticamente deviato.
27
2.17.3
Legge dei punti coniugati e ingrandimento
Come per gli specchi è possibile ricavare una legge che coinvolge le posizioni
p dell’oggetto e dell’immagine e la distanza focale f della lente:
1 1
1
+ =
p q
f
Tale legge è detta legge dei punti coniugati della lente. Se l’immagine è
reale q > 0 se è virtuale q < 0. Se la lente è convergente f > 0, se la lente è
divergente f < 0.
Inoltre si puo’ dimostrare che l’ingrandimento è dato da:
I=
q
p
.
Esempi
Un oggetto di 5 cm posto a 40 cm da una lente convergente avente focale di
10 cm; determinare la posizione e la dimensione dell’immagine.
Un oggetto di 20 cm posto a 200 cm da una lente divergente avente distanza
focale di 50 cm; determinare la posizione e la dimensione dell’immagine.
28
2.17.4
Le aberrazioni delle lenti
Consideriamo gli obiettivi delle macchine fotografiche. Per quale ragione si
dovrebbe usare un sistema di lenti, certamente più pesante e costoso di una
lente singola avente la medesima lunghezza focale? Vi sono molte ragioni
che spingono a costruire oculari, obiettivi, condensatori ed altri dispositivi,
combinando più lenti, ma una delle ragioni principali è per migliorare la
qualità delle immagini. L’immagine formata da un ’unica lente, infatti,
non puo’ essere immune da alcuni difetti detti aberrazioni; questo vale
anche per lenti costruite perfettamente. cioè senza disomogeneità nel vetro
e senza difetti superficiali o di curvatura. Ci sono 2 tipi di aberrazione:
l’aberrazione sferica e quella cromatica : l’aberrazione sferica è il fenomeno
per il quale i raggi di luce che passano per zone diverse di una lente sono
focalizzati in punti diversi in un’area detta ”cerchio di minima confusione”.
In generale avviene che i raggi marginali siano rifratti più fortemente dei
raggi prossimi all’asse ottico e, quindi, siano focalizzati più vicino alla lente
. Il fenomeno cresce più rapidamente di importanza con l’apertura della
lente; pertanto, se si vuole un ’immagine più nitida, bisogna restringere il
diametro, accontentandosi di un immagine meno luminosa.
L’aberrazione cromatica si verifica perchè i diversi colori che formano la
luce convergono in punti differenti.
2.17.5
La macchina fotografica
La macchina fotografica è sostanzialmente una camera oscura. La luce vi
entra da un’apertura (il diaframma) attraversando un sistema di lenti (l’obbiettivo) che la fa convergere sulla parete posteriore. Li si trova la pel
licola, su cui è depositata una sostanza sensibile alla luce. L’interno della macchina fotografica è al buio. Davanti alla pellicola vi è una tendina
l’otturatore che impedisce alla luce di entrare. Quando scattiamo una foto,
apriamo e chiudiamo rapidamente l’otturatore per consentire alla luce di entrare. Durante questo intervallo di tempo la pellicola rimane impressionata
registrando l’immagine dell’oggetto esterno. L’obbiettivo si comporta come
una lente convergente, forma un’immagine reale e capovolta dell’oggetto
fotografato. Per ottenere una buona fotografia, in cui l’immagine appare
nitida, è necessario che essa si formi esattamente sul piano della pellicola.
29
Affinchè ciò accada , un dispositivo di messa afuoco regola la distanza tra la
pellicola e l’obbiettivo, spostando quest’ultimo fuori e dentro. Le macchine
fotografiche più usate e più costose adottano il sistema reflex, che consiste
nel vedere attraverso l’oculare l’immagine che sta per essre registrata sulla
pellicola.
Uno specchio posto a 45◦ rispetto alla direzione dei raggi luminosi riflette
sull’oculare l’immagine formata dall’obiettivo, costituito da una complessa
serie di lenti. Quando l’immagine è a fuoco, si può scattare la fotografia. In
questo istante lo specchietto si solleva e l’immagine impressiona la pellicola.
Sull’obiettivo della macchina fotografica, oltre alla lunghezza focale, è
riportata solitamente l’indicazione dell’apertura massima. Questa è una
misura del rapporto tra il diametro utile delle lenti e la lunghezza focale
dell’obiettivo. E indicata come quoziente: per esempio la scritta 1 : 4 sta
a significare che la lunghezza focale è 4 volte il diametro dell’obiettivo. Un
obiettivo è tanto più luminoso quanto più grande è questo rapporto.
La quantità di luce che entra effettivamente nella macchina fotografica
è determinata dal tempo di esposizione e dall’apertura del diaframma. I
valori indicati sulla ghiera del diaframma sono stabiliti in modo che ogni
30
numero successivo corrisponda al dimezzamento della quantità di luce che
entra. Questa quantità è proporzionale all’area attraversata dalla luce e
quindi alle frazioni:
1
1/2
1/4
1/8
1/16
1/32
1/512
1/64
1/128
1/256
1/1024
Le radici quadrate di questi numeri sono proporzionali ai diametri del diaframma da usare. Se consideriamo i soli denominatori e ne calcoliamo la
radice quadrata (troncando alla seconda cifra), otteniamo la successione di
numeri:
1
1
4
2
2, 8
4
5, 6
8
11
16
22
32
che è quella comunemente usata in tutte le macchine fotografiche sulla
ghiera dei diaframmi per indicarne l’apertura.
2.17.6
Il cinematografo
Per il cinematografo sono necessari sia una macchina da presa che uno speciale proiettore. La macchina da presa è una macchina fotografica che scatta
una dopo l’altra numerose fotografie del soggetto (di solito 24 fotogrammi
al secondo), registrandole su una pellicola che scorre. Questa pellicola viene
poi sviluppata e stampata.
Il proiettore è dotato di un motore che fa avanzare la pellicola in modo
che in ogni secondo vengano proiettati successivamente diversi fotogrammi. Il nostro occhio percepisce un’immagine continua (e non a scatti, come
è in realtà), perché è incapace di distinguere cambiamenti di luce che si
susseguono troppo rapidamente.
Questo fenomeno, che si chiama persistenza delle immagini, è una caratteristica del nostro sistema visivo, che non riesce a distinguere due segnali
visivi troppo ravvicinati. Esso ha luogo, per esempio, quando si accende e
si spegne una lampadina molto rapidamente. Se la frequenza è maggiore
di 30 lampi al secondo, non si riesce più a seguire la variazione del segnale
luminoso e si ha l’illusione di luce continua.
2.17.7
Occhio
L’occhio è l’elemento di ingresso del nostro sistema visivo. Come una macchina fotografica, ha la capacità di riprendere l’immagine di oggetti esterni.
Tali immagini si formano sul fondo dell’occhio, dove si trova una superficie
coperta di elementi sensibili alla luce, la retina. I raggi luminosi emessi, o
31
diffusi, da un oggetto posto di fronte all’occhio passano attraverso una lente
convergente (il cristallino) che produce un’immagine sulla rètina.
Ma mentre la macchina fotografica esaurisce il proprio compito nella registrazione (passiva) delle immagini, l’occhio ha una funzione molto più complessa. Ha il compito di informare il cervello mediante un codice di segnali
nervosi, che vengono poi interpretati e tradotti in una rappresentazione degli
oggetti. Dagli impulsi nervosi il nostro cervello ricava gli elementi necessari
per costruire, secondo gli schemi della nostra attività mentale, l’immagine
dell’oggetto che guardiamo.
L’occhio ha la forma di un globo. È racchiuso da una spessa membrana
opaca, che presenta sul davanti una superficie trasparente detta cornea. Dietro di essa vi è l’iride, un diaframma che ha nel centro un foro (la pupilla)
attraverso cui penetra la luce. La pupilla è unconsciamente comandata da
un muscolo che ne regola il diametro (da circa 2 a 9 millimetri), secondo
l’intensità della luce incidente. Lo spazio tra la cornea e l’iride è pieno di
un liquido trasparente, che si chiama umor acqueo. A contatto con l’iride,
nella sua parte posteriore, vi è il cristallino, un corpo trasparente a forma
di lente, circondato dal muscolo ciliare. Tutto lo spazio dietro al cristallino
è pieno di una sostanza gelatinosa trasparente, l’umor vitreo. Nell’occhio si
susseguono quindi tre mezzi rifrangenti:
1. la cornea e l’umor acqueo, che hanno la stessa densità.
2. il cristallino che ha una maggiore densità della cornea
3. l’umor vitreo che ha la stessa densità dell’umor acqueo.
Quando guardiamo un oggetto luminoso o illuminato, alcuni degli infiniti
raggi di luce emessi in tutte le direzioni dai suoi diversi punti penetrano attraverso la pupilla nell’occhio. Dopo essere stati rifratti dai mezzi trasparenti
che incontrano, essi formano un’immagine reale dell’oggetto sulla retina. Il
cristallino è una lente, la cui distanza focale può variare per azione del muscolo ciliare che, contraendosi, modifica i raggi delle sue superfici. E questo
32
ii meccanismo dell’accomodamento, cioè della possibilità che ha l’occhio di
formare sulla rètina immagini nitide di oggetti che si trovano a diverse distanze. Quando l’occhio normale è in riposo, il muscolo ciliare è rilasciato e il
cristallino ha la curvatura minima: si dice allora che l’occhio è accomodato
all’infinito (punto remoto). Contraendo il muscolo ciliare, si può fare aumentare la curvatura del cristallino fino a formare sulla rètina l’immagine
nitida di oggetti che si trovano alla distanza di circa 15 centimetri dall’occhio
(punto prossimo). Per giungere però a vedere distintamente a tale distanza è
necessario un certo sforzo, mentre senza fatica sensibile l’occhio può restare
a lungo accomodato a una distanza di 25 centimetri (distanza della visione
distinta).
2.17.8
Presbiopia, miopia, ipermetropia
La distanza del punto prossimo aumenta notevolmente con l’età, a causa del
progressivo irrigidirsi del cristallino. Questa perdita del potere di accomodamento con l’età si chiama presbiopia. Nell’occhio normale l’immagine di un
oggetto posto molto lontano si forma sulla rètina. Nell’occhio miope, invece,
l’immagine si forma prima della rètina e in quello ipermètrope dietro di essa. Questi due difetti della visione si correggono ponendo davanti all’occhio
una lente, che riporta l’immagine esattamente sulla rètina. Poiché nell’occhio miope il sistema è troppo convergente, la miopia si corregge con una
lente divergente. Nell’occhio ipermètrope, invece, il sistema è troppo poco
rifrangente. Perciò l’ipermetropia si corregge con una lente convergente.
2.17.9
Il microscopio e il cannocchiale
Nella sua forma più semplice il microscopio è costituito da 2 lenti convergenti: l’obiettivo e l’oculare. L’oggetto AB, che si vuole osservare, si trova
appena al di là del fuoco F1 dell’obiettivo. Questa lente forma una prima immagine A1 B1 , reale, capovolta e ingrandita in una posizione intermedia tra
l’oculare e il suo fuoco F2 . A sua volta l’oculare trasforma la prima immagine in una seconda immagine A2 B2 che è virtuale, diritta rispetto ad A1 B1
33
(e quindi capovolta rispetto all’oggetto) e ingrandita. Guardando attraverso l’oculare si vede cosı̀ un’immagine ingrandita dell’oggetto, che si forma
a una distanza dall’occhio pari alla distanza della visione distinta. Con i
migliori microscopi si ottengono ingrandimenti di circa un migliaio di volte
e si possono esaminare oggetti le cui dimensioni sono dell’ordine del micron,
cioè di un millesimo di millimetro. Oggetti di questa dimensione sono, per
esempio, i batteri. Il cannocchiale astronomico consiste in un tubo metallico che porta ai due estremi opposti un obiettivo e un oculare. L’obiettivo
è una lente convergente di grande diametro e di grande distanza focale. Se
l’oggetto che si osserva è molto lontano, l’obiettivo ne forma un’immagine
reale e capovolta A1 B1 , nel piano che passa per il suo secondo fuoco F10 .
Regolando la lunghezza del tubo, si fa in modo che tale immagine si formi
tra il primo fuoco F2 dell’oculare e l’oculare stesso. Questo funziona allora come una lente di ingrandimento, ossia dà luogo a una immagine A2 B2
virtuale, ingrandita e diritta dell’immagine reale A1 B1 , data dall’obiettivo.
L’occhio dell’osservatore posto vicino al secondo fuoco F20 dell’oculare vede
tale immagine virtuale, la quale è capovolta rispetto all’oggetto. I cannocchiali terrestri sono fatti inserendo lungo il percorso dei raggi, nell’interno
del tubo di un cannocchiale astronomico, un sistema di prismi o di lenti che
rovescia una seconda volta l’immagine (in modo che l’immagine finale sia
diritta). I binocoli sono costituiti da due cannocchiali terrestri fissati l’uno
all’altro alla distanza degli occhi.
3
Natura ondulatoria della luce
Non molti sanno esattamente cos’è la luce, e gli stessi scienziati hanno impiegato un bel po’ di tempo per venirne a capo. Noi cercheremo di ripercorrere
34
la strada che la scienza a seguito per arrivare a delle ipotesi, quali vere, quali
false che ci hanno permesso di oggi di spiegare in modo adeguato il come e
il perchè dei principali fenomeni luminosi che si presentano ai nostri sensi.
Prima però è doveroso
4
Il colore
Abbiamo introdotto l’argomento colore mostrando che la luce bianca passando attraverso il prisma si scompone in una successione continua di colori.
I ragazzi avevano il compito di individuare i vari colori a partire dal rosso.
Figura 5: Prisma
Hanno quindi riconosciuto che lo SPETTRO era formato da (rosso, arancione, giallo, verde, azzurro, indaco e violetto). L’unico problema è stato
dare un nome all’indaco, colore che per alcuni assomigliava ad un viola e
per altri ad un blu.
4.1
Esperimento sulla sintesi addittiva dei colori
Questo esperimento è stato svolto direttamente all’interno della mostra
”Fisicamente divertente” ed aveva lo scopo di far notare ai ragazzi che
mescolando luce rossa , blu e verde si possono ottenere dei colori diversi.
Materiale:
35
• Scatola metallica con 3 faretti (rosso, verde e blu)
• cartoncino bianco alla base della scatola
Abbiamo acceso contamporaneamente tutti 3 i faretti e i ragazzi hanno potuto notare che la il cartoncino appariva bianco. Poi abbiamo acceso
solamente il faretto rosso e quello verde e il cartoncino appariva giallo, poi
abbiamo acceso il faretto rosso e quello blu e il cartoncino era di colore magenta ed infine abbiamo acceso i faretti blu e verde e il cartoncino appariva
di colore azzurrino (ciano).
4.2
Esperimento sulla sintesi sottrattiva dei colori
Figura 6:
Per completare l’argomento in classe abbiamo utilizzato la solita scatoletta dell’ EDT per svolgere alcuni asperimenti sulla sintesi sottrattiva dei
colori.
Materiale:
• Proiettore
• Filtri ciano magenta e giallo
• Cavaliere
• Porta diapositive
Montaggio: predisporre l’apparecchiatura come nell’illustrazione. Sul
porta diapositive verranno portati rispettivamente i diversi filtri.
Esperimento: Guardare attraverso ciascun accoppiamento di filtri ed annotare i colori nuovi che si ottengono, sottraendo alla luce bianca le radiazioni
assorbite da ogni filtro. Osservare in particolare cosa si ottiene con l’uso
contemporaneo dei 3 filtri sottrattivi.
Conclusioni:Nella sintesi sottrattiva i colori base sono : ciano, giallo e magenta. Dal loro uso congiunto si ottengono i colori osservati sperimentalmente:
I ragazzi non hanno avuto alcuna difficoltà nell’individuare i colori da
inserire.
36
Colore dei filtri
Ciano e giallo
Magenta e giallo
Ciano e magenta
4.3
Colore risultante
......
......
.......
Il colore dei corpi
Figura 7: Colore dei corpi
Materiale
• Proiettore
• Schermo bianco
• Cavaliere per banco ottico
• Cavaliere per proiettore
• Porta diaframma
• Filtri colorati
• 2 Striscie di carta colorata rossa, blu e verde.
Il meccanismo della percezione dei colori (visione colorata) é un problema
ancora da risolvere, anche se molti scienziati si sono dedicati a questa ricerca; la sensazione cromatica é strettamente legata alla sensibilità dell’occhio
umano e, pertanto, la valutazione dei colori é un fatto soggettivo. Ciò malgrado, partendo dalle osservazioni effettuate negli esperimenti precedenti ,
che di rifanno alla teoria della TRICROMIA di Maxwell, é possibile spiegare
perché tutti i corpi appaiano del colore, che noi attribuiamo a ciascuno, pur
essendo illuminati con la stessa luce (quella del sole).
Montaggio: predisporre l’apparecchiatura secondo l’illustrazione.
Attaccare allo schermo tre stricie di carta (una rossa, una blu, una verde) poi
disporlo sul banco ottico mediante il cavaliere con fenditura. All’estremità
sinistra del banco sistemare il proiettore con l’apertura circolare rivolta allo
37
schermo ; davanti al proiettore disporre il portalenti corredato del portadiapositive, nel quale dovranno essere montati successivamente i filtri richiesti
dalle varie prove.
Alimentare il proiettore a 12 V ed illuminare lo schermo posto ad una distanza di circa cm 40 dal diaframma portalenti.
Esperimento 1: Montare il filtro rosso sul porta-diapositive, accendere il
proiettore ed osservare come si presentano le tre striscie colorate. Annotare
il tipo di luce usata ed il colore di ciascuna striscia, quando é illuminata con
tale luce.
Esperimento 2 : Sostituire il filtro rosso con il filtro bleu e ripetere le osservazioni con le relative note.
Esperimento 3 : sostituire il filtro bleu con il filtro porpora e ripetere le
osservazioni, annotandole con cura.
Esperimento 4 : illuminare le striscie di carta colorata con la luce bianca
(derivante, come é noto, dalla mescolanza di tutti i colori).
Dopo aver raccolto le osservazioni dei ragazzi è incominciata abbiamo
quindi tratto le seguenti conclusioni.
Conclusioni : per spiegare le osservazioni fatte nelle varie prove occorre anzitutto ricordare che i filtri sono trasparenti ad una banda di radiazioni piuttosto stretta (quella corrispondente al loro colore), mentre assorbono tutte le
altre componenti della luce bianca: cosı̀, ad esempio, il filtro rosso trasmette
la sola luce rossa ed il filtro bleu la sola luce bleu, ecc..
Quando si illuminano le striscie di carta rossa, blu e verde con la luce rossa,
nella quale sono presenti le radiazioni corrispondenti al bleu ed al verde,
la striscia rossa appare chiara in quanto riflette la luce rossa, mentre le le
striscie bleu e verde risultano scure, poiché assorbono totalmente la stessa
luce. In luce blu la striscia rossa appare scura in quanto assorbe questa
radiazione e, mancando il rosso, essa non può riflettere tale banda di colore.
Con il filtro porpora, che deriva dalla mescolanza additiva di rosso e di bleu,
risultano visibili le striscie rossa e bleu, mentre appare scura la striscia verde
in quanto la componente verde manca nella luce porpora.
In luce bianca le tre striscie di carta appaiono rispettivamente rossa, bleu
e verde, poiché ciascuna di esse riflette il colore di competenza, mentre assorbe tutte le altre componenti. La sensazione che si ha del colore dei corpi
é dovuta al tipo di radiazione luminosa che ciascun corpo diffonde per riflessione.
In mancanza di proiettori, filtri ecc. si puo’ utilizzare delle normalissime
torcie ed utilizzare come filtri fogli di cellophane di coloro diversi.
38
5
Visione
Se, da un lato, la scienza ha realizzato macchine e strumenti di grande perfezione, che nell’ultimo secolo hanno permesso di spiegare i più reconditi
segreti della natura attraverso l’esame della luce che la materia è capace
di emettere o di assorbire, dall’altro lato è vero che lo strumento ottico
più straordinario e complesso a disposizione dell’uomo è nato con lui: l’occhio, naturalmente, insı́eme a quella meravigliosa macchina che è il sistema
nervoso e che presiede alla elaborazione dei dati che provengono dal nervo
ottico. Con la visione dell’occhio umano, si entra in una sfera di percezioni
che sfuggono alla fredda e rigorosa obiettività dei dati di osservazione, per
coinvolgere sottili e spesso misteriosi comportamenti soggettivi ed esperienze personali o ancestrali. Percezioni che portano al di là dei dati sensoriali,
dando all’immagine forme e significati più vari e articolati.
Figura 8: Un effetto dovuto alla nostra abitudine alla terza dimensione: le
3 ragazze sembrano di statura crescente da sinistra a destra
Figura 9: Un esempio di bistabilità della percezione visiva. Si contano 6 o 7
cubi a seconda che si immagini di guardare la figura dall’alto verso il basso
o dal basso verso l’alto
Effetti imprevedibili e curiosi sono possibili con i colori: di essi varrà
39
Figura 10: Nell’immagine si contano delle macchie grigie nei punti in cui i
segmenti bianchi si incrociano. Rimane esclusa dall’effetto l’intersezione su
cui si fissa l’attenzione. Si tratta di un aspetto del contrasto di luminosità.
Figura 11: La percezione dei contorni inesistenti per i 2 triangoli è un altro
effetto illusurio associabile in parte alla nostra tendenza a vedere oggetti
semplici
pena di occuparsi con una certa attenzione, perchè presentano importanti
applicazioni in campo figurativo.
5.1
Visione stereoscopica
II mondo in cui viviamo è fatto di tre dimensioni. Per muoverci in esso
abbiamo bisogno di valutare la profondità dello scenario che ci circonda. Un
oggetto, diciamo un ostacolo, deve essere indı́viduato non solo in base alla
sua larghezza e alla sua altezza, ma anche alla sua forma e alla distanza che lo
separa da noi. Cimentatevi in una celebre prova: ponete sul tavolo di fronte a
voi un oggetto ritto in piedi, come una candela o una bottiglia. Chiudete ora
un occhio e con una mossa rapida, muovendo la mano dall’alto verso il basso,
toccate col dito indice l’orlo della bottiglia o lo stoppino della candela. Se
arrivate al bersaglio si tratta di un puro caso. In genere ci andrete solo vicini.
L’errore, naturalmente, non sarà troppo grande, per l’abitudine che abbiamo
a fare gesti di questo genere. Se poi possedete un gattino e vi va di fare
qualcosa di più complicato (e un tantino cattivo), provate a mettergli una
benda su uocchio e a farlo giocare con una pallina di stagnola appesa a un
40
filo. È poco probabile che la bestiola trovi la cosa granché divertente, perché
la pallina continuerebbe a sbattergli sul naso o dove nessuno se l’aspetta.
Ecco il perché dei due occhi che madre natura ci ha dato. Ca me due orecchie
ci consentono di individuare la provenienza di un suono, grazie alla sia pur
lieve differenza nei tempi in cui esso , le raggiunge, cosı̀ due occhi ci danno
immediatamente il senso della distanza e della profondità perché forniscono
al cervello due immagini differenti, nel senso che sono viste secondo due
angolazioni leggermente diverse. È facile verificarlo osservando un oggetto
alternativamente ora con un occhio, ora con l’ altro. La diversità e tanto più
evidente, quanto più l’ oggetto ci sta vicino, perché l’angolo che esso forma
con ı́ nostri occhi è maggiore. E’ quello che sı́ ma effetto stereoscopico.
Non è il caso di addentrarci sui meccanismi in base ai quali il cervello,
partendo da una coppia di immagini bidimensionali, come sono quelle che
si formano sulle retine, riesce a compiere questa prodigiosa ricostruzione
tridimensionale di ciò che viene osservato. Basterà notare che, a differenza di
quanto avviene per il suono, per la grande velocità propria della luce il nostro
sistema nervoso riceve le due immagini pressoché simultaneamente, ne valuta
le differenze, e le pone in relazione alla distanza che separa gli occhi tra loro
e naturalmente alla convergenza che essi devono assumere per focalizzare
lo sguardo sull’oggetto. E tanto gli basta, allenato com’è da esperienze che
si ripetono ogni giorno fin da giovane per trarre conclusioni assolutamente
precise. Provate ora a toccare la bocca della bottiglia tenendo ambedue
gli occhi aperti. Se non siete sbronzi, cosa che comporterebbe uno stato di
funzionamento anomalo del vostro sistema nervoso, non fallirete un colpo.
Una bella verifica del meccanismo della visione stereoscopica si può fare
fotograficamente, usando una macchina stereoscopica, che è una macchina
con due obiettivi affiancati che permettono di ottenere dello stesso oggetto
due fotografie un po’ diverse come le immagini che vengono ricevute dai
nostri occhi. Queste fotografie si chiamano stereogrammi. Guardiamo ora i
Figura 12: Stereogrammi osservati al museo di scienze naturali con uno
stereoscopio
due stereogrammi con un visore stereoscopico. Questo aggeggio fu inventato
nel 1832 dall’inglese Wheatstone. Usato nel modo corretto , esso permette
di far giungere l’immagine fotografata dall’obiettivo destro all’occhio destro
e l’altra all’occhio sinistro. Apparecchietti del genere sono in commercio, e
41
vengono spesso usati per osservare in tre dimensioni diapositive di interesse
turistico, come paesaggi, monumenti, statue, o magari ragazze poco vestite.
La profondità della scena appare straordinaria, si direbbe quasi più che se
la vedessimo dal vivo. Il cervello utilizza la grande somiglianza delle due
immagini per fonderle in una sola, e le lievi differenze che ci sono fra esse
per ricrearne la profondità.
Figura 13: stereoscopio
Possiamo divertirci a sovvertire l’ordine naturale delle cose, per esempio
invertendo di posto le due fotografie, in modo che l’immagine destinata all’occhio destro pervenga invece a quello sinistro e viceversa. Avremo cosı̀
una visione pseudoscopica, che ci fa apparire più vicino ciò che è più lontano.
Provate a pensare di muovervi per una stanza usando uno speciale binocolo che produce tale scambio delle immagini. Possiamo fabbricarcene uno,
seguendo lo schema della figura 14. Una scatola e quattro semplici specchietti bastano a creare l’inversione dei fasci luminosi. C’è sicuramente di che
divertirsi! Ma rimettiamo le cose al posto giusto. La coppia di disegni della
Figura 14: Pseudoscopio
42
figura 13 esemplifica tutto il discorso dell’effetto stereoscopico nel modo più
semplice possibile. Provate a far arrivare ciascuna immagine separatamente
a uno dei due occhi. Per riuscire nell’intento, ponete un cartoncino di circa venti centimetri in piedi verticalmente sul piano della pagina, in mezzo
alle due immagini, e appoggiateci sopra il naso evitando di fare ombra sul
foglio. A questo punto ”strabicate” gli occhi fino a portare i due punti neri
a sovrapporsi esattamente. È importante, per ottenere questo, non inclinare
la testa di lato. Se siete bravı́, dopo qual che tentativo, osserverete che il
quadrato più piccolo appare sollevato dalla pagina e decisamente più vicino
a voi. Si è manifestato appunto l’effetto stereoscopico di profondità, dovuto
alla piccola differenza tra le due immagini. Il quadrato minore nell’immagine
di sinistra è spostato un po’ a destra, e viceversa. Ciò fa sı̀ che esso sia visto
dai nostri occhi sotto un angolo differente che non il quadrato maggiore. È
un trucchetto in verità un po’ rudimentale, che mette a dura prova la nostra pazienza. Ma rende bene l’idea. Certo l’effetto sarebbe più convincente
se potessimo osservare le due immagini con un vı́sore stereoscopico. Potete
provare a costruirne uno, cosı̀ da poter fare tanti giochetti divertenti sul tipo
di quello dell’inversione degli stereogrammi di cui abbiamo detto poc’anzi.
5.2
Camera distorta di Ames
Un americano della California è l’ideatore della strana camera mostrata nella
figura ??, la quale illustra esemplarmente quanto ingannevole possa essere
la nostra percezione in peculiari ambientazioni.
La camera ha una forma bizzarra: in particolare il lato DG è alquanto
più lungo del lato CF e la finestra sulla sinistra è maggiore di quella sulla
destra. Tali differenze scompaiono se si osserva la camera con un occhio solo
attraverso un piccolo foro sulla parete frontale. Al contrario, due persone
in piedi negli angoli opposti sembrano molto diverse di statura, e l’effetto
è cosı̀ realistico da lasciare l’osservatore senza parole. La spiegazione sta
nell’attitudine del nostro sistema occhio-cervello a valutare la dimensione
degli oggetti tarando rispetto alla distanza l’immagine che si forma sulla
43
Figura 15: Camera di Ames
retina (una persona che si allontana produce sulla retina un’immagine che
va gradualmente rimpicciolendosi, ma non per questo la si giudica in continua contrazione). Nella camera di Ames, le due persone addossate agli angoli
si trovano a distanze diverse da chi osserva, ma il particolare disegno della
camera, unito alla perdita della stereoscopia per effetto della visione monoculare, non permette all’osservatore di accorgersene, cosicché egli valuta le
dimensioni di ciò che vede in modo del tutto sviato. La camera di Ames
fa giustizia completa di tanti pregiudizi legati a inganni dei nostri sistemi
percettivi.
5.2.1
Modalità costruttive
Il disegno nella figura 15 è abbastanza autosufficiente, ma per chi Volesse
costruirsi una camera di Ames a casa propria con riga e squadra, spieghiamo
meglio e proviamo a dare delle possibili misure. I calcoli si fanno tenendo
presente il fatto che, una volta annullato l’effetto di profondità, sulla retina
si produce una stessa immagine per tutte le pareti di fondo della camera
che sono inscritte in una piramide avente per vertice il foro di osservazione
e per base la parete normale, come suggerito dalla figura 2. Ci riferiamo
a una camera di dimensioni naturali, ma si può realizzarne una in formato
ridotto dove introdurre dei pupazzetti al posto delle persone scalando proporzionalmente tutte le dimensioni (proponiamo una riduzione di 10 volte e
l’uso di un pezzo unico di cartone robusto di colore chiaro). Due delle pareti
sono rettangoli, le altre due, il pavimento e il soffitto sono trapezi, come
mostrato nella figura 17. L’illuminazione della camera deve essere buona e
uniforme, come si può ottenere con una lampada al neon posta al soffitto
sopra il foro di osservazione (nel caso del modello ridotto si può realizzare
la camera a cielo aperto). Si noti che l’altezza dello spigolo AD è quasi il
doppio di quella dello spigolo BC, come lo è la sua distanza dal foro di osservazı́one. Però l’immagine dei due spigoli che viene a formarsi sulla retina
è di eguale altezza. Lo stesso dicasi per le due finestre dipinte sulla parete di
fronte. Per tracciarle nel modo corretto ci si avvalga, come suggerito nella
figura, di due linee di fuga a e b portate dal punto O di convergenza dei lati
44
Figura 16: L’effetto base dell’illusione: viste con un occhio solo le 2 pareti
appaiono della stessa forma
AB e DC della parete. Un miglior risultato si ottiene, ma l’operazione non
è strettamente indispensabile, dipingendo il pavimento a scacchi bianchi e
colorati con lo stesso criterio di distorsione applicato alle due finestre (si utilizzi il punto di fuga O’ riportato nella figura 16). Per aumentare l’illusione,
si può disegnare sulla parete un orologio, distorto nel modo consueto. Allo
scopo di compensare eventuali errori, è infine consigliabile praticare più di
un foro d’osservazione e scegliere poi quello che dà l’effetto più vicino alla
perfezione.
Figura 3.
Figura 17: Dimensioni in centimetri delle pareti e del pavimento della
camera distorta di Ames. Il soffitto ha le stesse dimensioni del pavimento.
Per le condizioni prescelte, illuminazione adeguata e uniforme delle pareti
contro le quali si stagliano le sagome scure delle persone, nel campo visivo
dell’osservatore mancano termini di paragone ambientale che lo rendano
edotto della diversa distanza dalle due figure (per solito l’immagine retinica
45
di un oggetto più lontano è meno luminosa e nitida, fattori che qui vengono
resi secondari). Il fatto di guardare con un occhio solo, infine, rende inoperante il principale meccanismo che ci permette di giudicare quale distanza
ci separa da un oggetto, ossia l’angolo formato dai 2 raggi visivi diretti agli
occhi. Il cervello allora prende alla lettera la dimensione delle immagini
che si formano sulla retina e capovolge la sua diagnosi, concludendo che la
persona a sinistra della figura 15 è pi piccola dell’altra.
46