Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Aurelia Orlandoni
Nuclei: Misure, dati e previsioni; Relazioni e funzioni
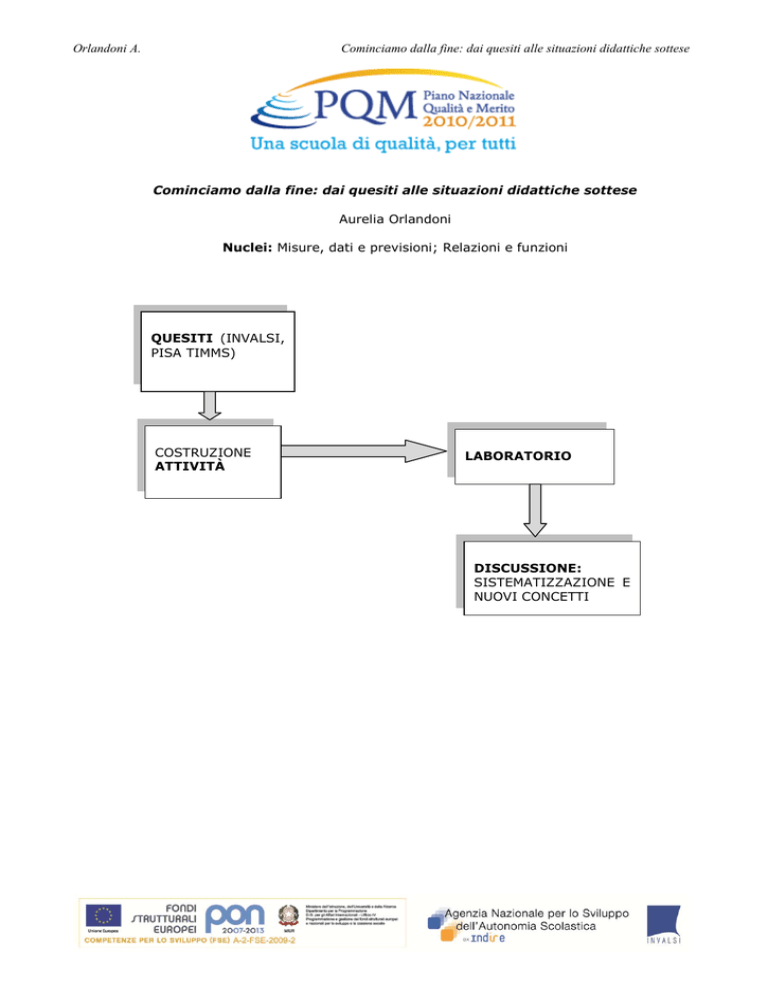
QUESITI (INVALSI,
PISA TIMMS)
COSTRUZIONE
ATTIVITÀ
LABORATORIO
DISCUSSIONE:
SISTEMATIZZAZIONE E
NUOVI CONCETTI
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Introduzione
Tematica
L’analisi delle prove di rilevazione degli apprendimenti nazionali e internazionali, oltre che
un’occasione per riflettere, può essere utilizzata dagli insegnanti per costruire “situazioni
didattiche”. A partire da alcuni quesiti viene proposta un’attività da sviluppare con la classe.
Finalità e obiettivi di apprendimento
Obiettivi in relazione alle Indicazioni 2007:
In situazioni concrete, di una coppia di eventi intuire e cominciare ad argomentare qual
è il più probabile, dando una prima quantificazione, oppure riconoscere se si tratta di
eventi ugualmente probabili
- Costruire, interpretare e trasformare formule che contengono lettere per esprimere in
forma generale relazioni e proprietà.
I traguardi per lo sviluppo della competenza coinvolti fanno riferimento a quelli proposti alla
fine della classe quinta della scuola primaria:
- Riesce a risolvere facili problemi (non necessariamente ristretti a un unico ambito)
mantenendo il controllo sia sul processo risolutivo, sia sui risultati e spiegando a parole
il procedimento seguito.
- Impara a riconoscere situazioni di incertezza e ne parla con i compagni iniziando a
usare le espressioni "è più probabile", “è meno probabile” e, nei casi più semplici,
dando una prima quantificazione.
Obiettivi specifici dell’attività:
1. Rappresentare situazioni problematiche
2. Matematizzare la situazione e fare congetture
3. Individuare strategie risolutive
4. Descrivere i procedimenti, argomentare le congetture e giustificare le scelte.
Metodologia
L’attività proposta vuole offrire spunti di lavoro per una metodologia di tipo laboratoriale 1
finalizzata, non tanto all’applicazione di concetti noti, ma alla costruzione di significati degli
oggetti matematici in gioco, anche non noti a priori. A questo scopo gli alunni, singolarmente
o in piccolo gruppi, affrontano le schede di lavoro proposte.
In una fase successiva , l’insegnante “conduce” una discussione matematica2 di classe.
Infine l’insegnante presenta una sintesi di tutto il lavoro approfondendo eventuali nuovi
concetti emersi.
1
Si fa esplicito riferimento alla definizione di Laboratorio di matematica di Matematica 2003-UMI: “… Il laboratorio
di matematica non è un luogo fisico diverso dalla classe, è piuttosto un insieme strutturato di attività volte alla
costruzione di significati degli oggetti matematici. Il laboratorio, quindi, coinvolge persone (studenti e insegnanti),
strutture (aule, strumenti, organizzazione degli spazi e dei tempi), idee (progetti di attività didattiche,
sperimentazione)…”
2
Si fa esplicito riferimento alla definizione di Discussione matematica di Matematica 2001-UMI: Una discussione
matematica è una polifonia di voci articolate su un oggetto matematico …
La discussione matematica dell’intera classe orchestrata dall’insegnante garantisce, con la presenza di quest’ultima, la
possibilità dell’articolazione di voci diverse da quelle degli allievi. L’insegnante ha un ruolo di guida nel senso che:
• Inserisce una particolare discussione nel flusso dell’attività della classe
• Influenza la discussione in modo determinante, inserendosi con interventi mirati nel suo sviluppo.
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Condizione, problema o stimolo da cui nasce l'attività
Le rilevazioni sui livelli di apprendimento dei quindicenni (Pisa, 2006), gli esiti della recente
“prova nazionale” nell’ambito degli esami di licenza media (legge 176/2007), le risultanze di
numerose indagini svolte a livello nazionale e regionale, attestano una palese criticità nelle
competenze degli allievi della nostra scuola nel campo degli apprendimenti matematici.
L’ampia presenza di debiti formativi in matematica nella scuola secondaria di II grado, trova
corrispondenza in una consistente area di insufficienza riscontrata nella scuola media (oltre il
20%), unito a prestazioni generalmente non brillanti (32% giudicati “sufficienti”). Questa
situazione, che si riverbera negativamente sulle possibilità di successo formativo degli studenti,
richiede una presa di coscienza generalizzata del problema, un’adeguata riflessione da parte
degli insegnanti e l’adozione di coerenti strategie didattiche (rinnovamento dei metodi di
insegnamento, analisi delle modalità di valutazione, eventuali iniziative di recupero, messa a
punto di curricoli disciplinari coordinati, ecc.).
Oltre a questo è importante ricordare che diversi studi che cercano di indagare quali possano
essere gli elementi che determinano il successo dei sistemi scolastici che ottengono risultati
migliori nelle prove PISA sottolineano, fra gli altri aspetti, che l’insegnamento della matematica
privilegiato in quelle realtà adotta una metodologia di “problem solving”.
Infine le Indicazioni curricolari definiscono quale idea di matematica è sottesa ai traguardi per
lo sviluppo della competenza, sottolineando sia l’aspetto strumentale sia quello culturale. È
importante ricordare che vi è una forte unitarietà per il primo ciclo: l’idea di matematica è la
stessa per la scuola primaria e per la secondaria di 1° grado. Sono anche fortemente intrecciati
i contenuti disciplinari, le situazioni e i contesti in cui i problemi sono posti, i processi che
gli allievi devono attivare per collegare la situazione problematica affrontata con i contenuti
matematici.
Prerequisiti richiesti ai ragazzi per svolgere l’attività
Non vi sono prerequisiti particolari per lo svolgimento dell’attività, se non le conoscenze
elementari di matematica all’uscita della scuola primaria.
Strumenti forniti agli allievi
Vengono fornite schede di lavoro. Il lavoro può essere svolto con carta e penna, calcolatrici.
L’uso delle tecnologie può favorire sia la fase di lavoro individuale/di gruppo (calcolatrici,
computer e software per la matematica) sia la fase di discussione (LIM).
Organizzazione della classe e metodologia
Si sottolineano innanzitutto tre parole chiave dal punto di vista metodologico:
1. Laboratorio
2. Risolvere problemi
3. Riflettere sui propri percorsi di conoscenza
La classe dovrebbe essere organizzata per lavorare in piccoli gruppi nella prima parte di
ognuna delle due attività proposte (circa due ore), mentre la seconda parte (circa un’ora per
attività) dovrebbe essere dedicata ad una discussione orchestrata dall’insegnante.
Questo perché è fondamentale lasciare spazio e respiro alla fase di esplorazione e formulazione
di ipotesi/congetture.
A titolo indicativo si elencano alcuni elementi di attenzione per la fase di discussione:
L’insegnante analizza le schede prodotte dagli studenti annotandosi punti forti e punti
deboli da fare emergere nel corso della discussione
L’insegnante restituisce ai gruppi i loro lavori e chiede ad ogni gruppo di illustrare
brevemente quanto fatto
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
L’insegnante fa in modo che si sviluppi una discussione fra gli studenti e che non vi sia
un unico canale studente-insegnante
L’insegnante sottolinea gli elementi a suo avviso più importanti e interviene per
chiedere precisazioni e chiarimenti, annota alla lavagna i punti e gli elementi che
vengono via via condivisi senza avere “fretta di arrivare alla conclusione” ma dando
spazio e tempo affinchè vengano condivise le strategie, le osservazioni, …. E si arrivi ad
una sintesi pienamente condivisa
Fasi e tempi (indicativi)
FASE 1 - Misure, dati e previsioni (2 ore)
Nella scheda di lavoro per gli studenti vengono proposti due item modificati, uno di PISA e uno
della prova nazionale 2008. Le situazioni sono quelle originarie, mentre sono state modificate
le domande allo scopo di stimolare un lavoro di analisi ed esplorazione con la richiesta di
formulare congetture e rispondere a diverse domande. Ogni insegnante potrà selezionare, fra
quelle proposte, quelle che ritiene più adatte alla classe.
Ogni affermazione e ogni risposta devono essere spiegate e giustificate con cura dagli studenti
FASE 2 - Misure, dati e previsioni (1 ora)
L’insegnante, dopo avere analizzato i lavori degli studenti proporrà una discussione che metta
in evidenza punti forti e punti deboli emersi nei lavori. Il ruolo dell’insegnante in questa fase
deve essere quello di stimolare la discussione in modo da fare intervenire quanto più possibile
gli studenti e di guidare la discussione verso una sintesi comune e condivisa.
FASE 3 - Relazioni e funzioni (circa 2 ore)
Analoga alla Fase 1 ma con riferimento ad item diversi appartenenti ad un diverso nucleo
tematico
FASE 4 - Relazioni e funzioni (circa 1 ora)
Analoga alla Fase 2 ma con riferimento ad item diversi appartenenti ad un diverso nucleo
tematico
Materiali Allegati
1.
2.
3.
4.
5.
6.
Scheda
Scheda
Scheda
Scheda
Scheda
Scheda
attività Misure, Dati e previsioni
guida docente su attività Misure, Dati e previsioni
attività Relazioni e funzioni
guida docente su attività Relazioni e funzioni
test internazionali
risorse e strumenti con indice documentazione disponibile
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Attività Misure, Dati e previsioni- Scheda studenti
Nomi Studenti ___________________________________________ classe _____
RISULTATI DI UNA VERIFICA
Il grafico seguente mostra i risultati di una verifica di scienze, ottenuti da due gruppi di
studenti, indicati come Gruppo A e Gruppo B.
Il punteggio medio del Gruppo A è 62,0 e quello del Gruppo B è 64,5. Per avere la sufficienza,
gli studenti devono ottenere almeno 50 punti.
Nel rispondere alle domande seguenti ricordati che devi sempre:
Giustificare le risposte
Scrivere in modo chiaro e dettagliato il procedimento che hai seguito.
DOMANDE
……………………………………………………………..
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
In una grande libreria gli impiegati sono così suddivisi:
Mansione
Magazzinieri
Cassieri
Venditori
Contabili
Numero di
impiegati
4
8
2
.
Nel rispondere alle domande seguenti ricordati che devi sempre:
Giustificare le risposte
Scrivere in modo chiaro e dettagliato il procedimento che hai seguito.
DOMANDE
……………………………………………………………..
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Attività- Misure, dati e previsioni Scheda docente
Nella scheda per gli studenti è riportato la parte relativa allo stimolo di un quesito PISA
Di seguito vengono elencate alcune possibili richieste fra cui l’insegnante potrà selezionare
quelle che ritiene adeguate da sottoporre agli studenti:
1. Cosa significa questa rappresentazione? La conosci? Perché in ascissa c’è una coppia di
numeri e in ordinata uno solo? Cosa significano?
2. Mentre in gran parte del grafico ci sono due colonne affiancate (una grigia e una nera)
all’inizio invece ce n’è una isolata grigia e una isolata nera? È un errore? Cosa significa?
3. Quanti alunni per gruppo hanno meritato la sufficienza? Qual è la percentuale?
4. Quanti alunni per gruppo hanno meritato almeno la sufficienza? Qual è la percentuale?
5. Quanti alunni ci sono nel gruppo A? e quanti nel gruppo B?
6. Qual è il punteggio massimo che si poteva ottenere? E quello raggiunto dagli studenti?
7. Quanti punti hanno totalizzato gli studenti migliori del gruppo A? e nel gruppo B? e i
peggiori?
8. Qual è il gruppo più omogeneo? Qual è il gruppo migliore? Perché?
9. Se tu fossi un alunno in quale gruppo vorresti essere? Perché?
10. Quale sarà il gruppo migliore per l’insegnante? Perché? Prova a trovare argomenti per
sostenere che è meglio il gruppo A e altri per sostenere che è meglio il gruppo B
11. Qual è il punteggio più frequente nel gruppo ?A e nel gruppo B?
12. È possibile calcolare la media generale? Come?
13. Secondo voi la prova era facile o difficile? Perché?
14. È più probabile che abbia ottenuto un punteggio compreso fra 60 e 69 un alunno del
gruppo B o del gruppo A? Perché?
15. Qual è la probabilità che abbia avuto più di 70 punti un alunno del gruppo A? e un
alunno del gruppo B?
16. Qual è la probabilità che uno studente del gruppo A abbia ottenuto almeno la
sufficienza? E nel gruppo B?
17. E’ possibile ricavare le tabelle relative ai dati originali? Come?
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
L’insegnante valuterà, tenendo conto del contesto, quali e quante domande selezionare e
inserire nella scheda studente.
Potrà anche decidere di inserire molte domande e chiedere agli studenti di selezionarne un
certo numero su cui concentrare l’attenzione e sviluppare il lavoro, spiegando i motivi della
scelta. In questo caso i tempi però verrebbero senz’altro dilatati e più che un’attività il lavoro
potrebbe portare a sviluppare un percorso.
Per completezza si riporta il quesito che era proposto nel PISA e l’analisi delle risposte degli
studenti:
In base a questo grafico, l’insegnante sostiene che, nella verifica, il Gruppo B è andato meglio
del Gruppo A.
Gli studenti del Gruppo A non sono d’accordo con l’insegnante. Essi cercano di convincere
l’insegnante che il Gruppo B non è necessariamente andato meglio.
Con l’aiuto del grafico, suggerisci agli studenti del Gruppo A una spiegazione matematica che
potrebbero usare.
È importante sottolineare che la richiesta non è usuale per i nostri studenti e che le risposte
corrette sono state il 15,3% (media OCSE 31,3%) con una percentuale di omissioni pari al
54,7% (media OCSE 34%).
Un’analisi del problema è proposta nella presentazione RISULTATI DI UNA VERIFICA.PDF
La seconda situazione proposta è tratta dalla prova nazionale alla fine del primo ciclo del 2008
Seguendo la stessa traccia della situazione precedente, vengono proposte una serie di
domande fra cui selezionarne alcune:
1. È possibile individuare il numero (mancante) dei magazzinieri? Come?
2. Se i venditori rappresentassero il 32% quanti sarebbero i magazzinieri?
3. Potrebbero i cassieri rappresentare il 40% degli impiegati? Perché?
4. Calcola il numero dei magazzinieri e completa l’areogramma con tutte le percentuali
Nel quesito originario si chiedeva di calcolare il numero dei magazzinieri.
Diversi sono state le strategie utilizzate dagli studenti, ad esempio:
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Riduzione all’unità: Se i venditori sono il 40% i contabili allora sono il 10 (vedi grafico)
che corrispondono a 2 persone, quindi il totale deve essere 20 e quindi i magazzinieri 6
La metà degli impiegati è 10 persone. Quindi 10-4 (cassieri) = 6
….
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Attività Relazioni e Funzioni- Scheda studenti
Nomi Studenti___________________________________________ classe _____
La figura mostra le orme di un uomo che cammina. La lunghezza P del passo è la distanza tra
la parte posteriore di due orme consecutive.
Per gli uomini, la formula
=140 fornisce una relazione approssimativa tra n e P
dove:
n = numero di passi al minuto, e
P = lunghezza del passo in metri.
Oppure
Per gli uomini, la formula n=140*P fornisce una relazione approssimativa tra n e P
dove:
n = numero di passi al minuto, e
P = lunghezza del passo in metri.
CONSEGNE
…………………………………………….
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
D4 Se n è un numero naturale qualsiasi, quale formula devi usare per essere sicuro di
trasformare n sempre in un numero dispari?
A.
B.
C.
D.
n 1
n 1
n 2 1
n
1
2
1. Scrivi il ragionamento che hai seguito per scegliere la formula corretta.
2. Perché hai scartato le altre formule?
D18. Scrivi la formula che esprime come varia l’area A della figura qui di fianco, al variare della
lunghezza a.
A = ___________________
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Attività Relazioni e Funzioni- Scheda docenti
Qui l’obiettivo è avviare ad un primo approccio al significato di variabile, considerandone due
accezioni:
Variabile funzionale, cioè una variabile che dipende da un’altra, n è funzione di P, se n
aumenta, P diminuisce e viceversa.
Variabile intesa come qualcosa che sta al posto di un numero qualsiasi
Al termine dell’attività gli studenti dovrebbero avere colto la differenza fra i due significati ed
essere in grado di produrre qualche esempio. Non ci si aspetta che esprimano in modo formale
ma che abbiano colto i significati.
Il quesito è tratto da PISA. La parte inserita dopo “oppure” è una semplificazione che viene
proposta tenendo conto che La situazione è proposta in prima media e gli alunni potrebbero
non avere ancora trattato il concetto di rapporto, mentre quello di formula è già familiare dalla
scuola primaria.
Si possono ipotizzare attività diverse:
Chiedere agli studenti di verificare la formula operando delle misure reali su alcuni di
loro
Eliminare la parte contenente la formula e chiedere loro di cercare una formula
operando misure reali (in questo caso l’attività aprirebbe la strada ad un vero e proprio
percorso)
Porre loro la prima delle domande associate al quesito: Se la formula si applica
all’andatura di Enrico ed Enrico fa 70 passi al minuto, qual è la lunghezza del passo di
Enrico? Chiedendo di indicare in modo chiaro e dettagliato il procedimento seguito.
L’importante è che vengano proposti quesiti che introducano una prima riflessione sul
significato di variabile nei suoi aspetti funzionali.
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Anche qui per completezza viene proposta un’analisi del quesito e del suo possibile utilizzo
didattico (vedi ANDATURA.PDF)
Il quesito è tratto dalla prova nazionale 2009. Qui è stato semplificato il testo e sono state
inserite due domande.
Ci si aspetta che gli studenti facciano delle prove sostituendo diversi numeri nelle formule. A
questo scopo l’insegnante può decidere di inserire una tabella da completare in cui si invitano
gli studenti a sostituire dei numeri. È però importante che non venga indicato alcun numero da
cui cominciare, ma si lasci la scelta completamente libera. È proprio attraverso l’analisi delle
scelte operate che possono emergere spunti interessanti per la discussione.
Si potrebbe anche ipotizzare di proporre il quesito in forma aperta, ma è forse prematura in
prima media un’attività che abbia come scopo la costruzione di una formula e potrebbe forse
solo essere il punto di avvio per un percorso più lungo
Si riporta l’analisi del quesito pubblicata sul sito INVALSI
Domanda
D4.
Commento
D4
Se n è un numero
naturale qualsiasi, quale
procedimento devi seguire
per
essere
sicuro
di
ottenere sempre un numero
dispari?
Il
quesito
richiede
di
individuare una formula
per ottenere un numero
dispari a partire da un
numero naturale qualsiasi.
A.
È
stato
risolto
correttamente dall’86,8%
degli studenti, segno che
la scrittura algebrica dei
numeri dispari è nota agli
studenti.
Dalle Indicazioni per il
curricolo 2007: costruire,
interpretare e trasformare
B.
C.
D.
n 1
n 1
n 2 1
n
1
2
Quadro di Riferimento delle
prove INVALSI
OGGETTI DI VALUTAZIONE:
Classificazione di oggetti, figure,
numeri in base a una determinata
proprietà.
Rappresentazione
di
fatti
e
fenomeni attraverso tabelle, grafici
ed espressioni algebriche.
PROCESSI COGNITIVI:
Conoscere
e
padroneggiare
algoritmi e procedure (in ambito
aritmetico, geometrico...).
COMPITI:
Costruire, leggere e interpretare
formule.
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
formule che contengono
lettere per esprimere in
forma generale relazioni e
proprietà.
Generalizzare relazioni in una
sequenza
numerica
utilizzando
parole e lettere.
Proprio perché si ritiene che quest’attività potrebbe costituire l’avvio di un percorso di
approccio all’algebra, si ritiene utile riportare un altro quesito della prova del 2009, invitando
gli insegnanti ad analizzare con attenzione la consegna e il commento ai risultati.
D18.
Scrivi la formula che esprime come varia l’area A della figura qui di fianco, al variare
della lunghezza a.
A = ___________________
Dal commento sul sito INVALSI
“Il quesito richiede di individuare una formula relativa all’area A di una figura piana utilizzando
la variabile a. Nella pratica didattica non è usuale che ai ragazzi sia chiesto di individuare una
formula a partire da una variabile data.
I risultati confermano questa impressione in quanto solo il 26,8% risponde correttamente.
Questo fatto dovrebbe fare riflettere i docenti sul modo col quale nella scuola media si propone
l’approccio all’algebra. Non è tanto importante il calcolo algebrico in quanto tale, ma lavorare
sui significati di variabile anche legati a contesti noti ai ragazzi come in questo caso.
Per gli studenti le lettere nelle formule di geometria, come ad esempio A= bxh, non
rappresentano delle variabili ma sono semplicemente delle etichette, iniziali di area, base, ….”
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
RISORSE E STRUMENTI
Vengono allegati all’attività o alla parte comune a tutte le attività diversi materiali
utilizzabili dai docenti come approfondimenti:
1. Il Laboratorio di Matematica – MATEMATICA 2003, La Matematica per il cittadino, MIUR,
UMI e, SIS, Mathesis (allegato alla parte comune)
2. La discussione matematica in classe e Risolvere e porsi problemi - MATEMATICA 2001,
La Matematica per il cittadino, MIUR, UMI e, SIS (allegato alla parte comune)
3. Due presentazioni di approfondimento di problemi PISA: Andatura.pdf e Risultati di una
verifica.pdf
4. Il Laboratorio matematico-scientifico: suggerimenti ed esperienze, Supplemento al n. 8
di Innovazione Educativa, ottobre 2007
5. Le prove INValSI: un contributo per lo sviluppo degli apprendimenti di base,
Supplemento al n. 3/4 di Innovazione Educativa, marzo/aprile 2006
1. Un’analisi e commento alla prova di terza media 2009 scaricabile dal sito INVALSI
BIBLIOGRAFIA
AAVV,
per un
AAVV,
per un
AAVV,
per un
Matematica 2001. La matematica per il cittadino. Attività didattiche e prove di verifica
nuovo curriculo di matematica. Ciclo primario.
Matematica 2003. La matematica per il cittadino. Attività didattiche e prove di verifica
nuovo curriculo di matematica. Ciclo secondario.
Matematica 2004. La matematica per il cittadino. Attività didattiche e prove di verifica
nuovo curriculo di matematica. Quinta classe del ciclo secondario di secondo grado
Sono tutti scaricabili in formato pdf dal sito UMI,
http://umi.dm.unibo.it/iold/taliano/Didattica/didattica.html
sezione
Didattica,
all’indirizzo:
L. Bazzini, R. Iaderosa, 2000, Approccio all’algebra, Riflessioni didattiche, Franco Angeli, Milano
R. Garuti, A. Orlandoni e R. Ricci (a cura di), Il Laboratorio matematico-scientifico:
suggerimenti ed esperienze, Supplemento al n. 8 di Innovazione Educativa, ottobre 2007
(scaricabile in formato pdf all’indirizzo: http://www.irreer.it/rivista/index.html)
W. Maraschini, 2008, Bravi in matematica, Bruno Mondadori, Milano
OECD,2004, Pisa 2003 -Valutazione dei quindicenni, Armando Editore, Roma.
R. Zan, 1998, Problemi e convinzioni, Pitagora Editrice, Bologna
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
SITOGRAFIA
Molti materiali per costruire attività simili sono reperibili nel sito di ANSAS ex-INDIRE sia nella
sezione FOR Docenti sia all’interno della sezione dedicata al piano [email protected].
Il sito INVALSI contiene i testi delle prove rilasciate sia del sistema nazionale sia delle ricerche
internazionali (PISA e TIMMS)
Polymath, sito del Politecnico di Torino, in cui vengono proposti problemi. È ricco di
informazioni, materiali, proposte didattiche, indicazioni bibliografiche e sitografiche ed è
continuamente aggiornato.
Progetto ArAl – Percorsi nell’aritmetica per favorire il pensiero prealgebrico. Il progetto ArAl è
dedicato al rinnovamento dell’insegnamento dell’area aritmetico algebrica nella scuola
dell’obbligo. Presenta materiali strutturati e testati in particolare per la scuola primaria e
secondaria di 1° grado.
Matematicamente – Sito che contiene molti spunti di lavoro sia per gli insegnanti che per gli
studenti: esercizi, giochi lezioni,….
Orlandoni A.
Test internazionali
TIMMS 2003 IV primaria
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
TIMMS 2007 IV primaria
Le sezioni A e B hanno ognuna 40 alunni.
Nella sezione A ci sono più femmine rispetto alla sezione B. Quante ce ne sono
di più nella sezione A rispetto alla sezione B?
a) 14
b) 16
c ) 24
d) 30
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Orlandoni A.
TIMMS 2003 3 media
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Orlandoni A.
TIMMS 2007 3° media
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Orlandoni A.
PROVE RILASCIATE PISA
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
Orlandoni A.
Cominciamo dalla fine: dai quesiti alle situazioni didattiche sottese
PROVA SCARTATA DA PISA IN FASE PRETEST
BATTITO CARDIACO
Per motivi di salute, le persone dovrebbero limitare i loro sforzi, ad esempio durante le attività
sportive, per non superare una determinata frequenza del battito cardiaco. Per anni, la
relazione tra la frequenza cardiaca massima consigliata e l’età della persona è stata descritta
dalla seguente formula: Frequenza cardiaca massima consigliata = 220 – età
Recenti ricerche hanno mostrato che questa formula dovrebbe essere leggermente modificata.
La nuova formula è la seguente: Frequenza cardiaca massima consigliata = 208 – (0,7 ×
età)
Domanda 1 - Un articolo di giornale afferma: “Una conseguenza dell’uso della nuova formula
al posto della vecchia è che il numero massimo consigliato di battiti cardiaci al minuto
diminuisce leggermente per i giovani e aumenta leggermente per gli anziani”. A partire da
quale età la frequenza cardiaca massima consigliata diventa maggiore come risultato
dell’introduzione della nuova formula? Scrivi qui sotto i passaggi che fai per arrivare alla
risposta.
Domanda 2 - La formula frequenza cardiaca massima consigliata = 208 – (0,7 età)
viene usata anche per determinare quando l’esercizio fisico ha efficacia massima. Alcune
ricerche hanno mostrato che l’esercizio fisico ha la massima efficacia quando i battiti sono
all’80% della frequenza cardiaca massima consigliata.
Scrivi una formula che fornisca la frequenza cardiaca, in funzione dell’età, affinché l’esercizio
fisico abbia la massima efficacia.












