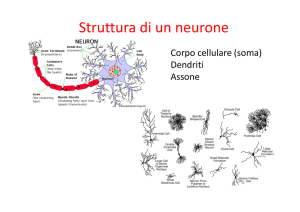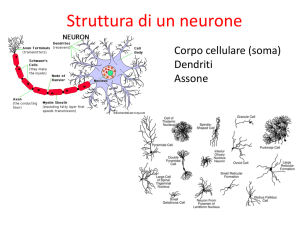
Il duello triangolare
Smith, Brown e Jones si accordano per un duello alla pistola con le seguenti condizioni.
Dopo aver tirato a sorte per stabilire chi tirerà per primo, secondo e terzo, essi si
dispongono ai vertici di un triangolo equilatero. L'accordo è che ognuno può tirare un
solo colpo ogni turno e che si continua nello stesso ordine ciclico sinché due siano
morti. Ad ogni turno l'uomo che tira può mirare dove preferisce. I tre duellanti sanno che
Smith colpisce sempre il bersaglio, Brown è preciso per l'80 % delle volte e Jones per il
50 %.
Ammettendo che tutti adottino la migliore strategia e che nessuno sia ucciso da un
colpo vagante non diretto a lui, quali sono le probabilità esatte di sopravvivenza dei tre?
______________________________________________________________________
Premessa
Valutiamo prima di tutto le probabilità di sopravvivenza che si hanno in un normale
duello a due. Siano:
§
§
§
§
§
§
§
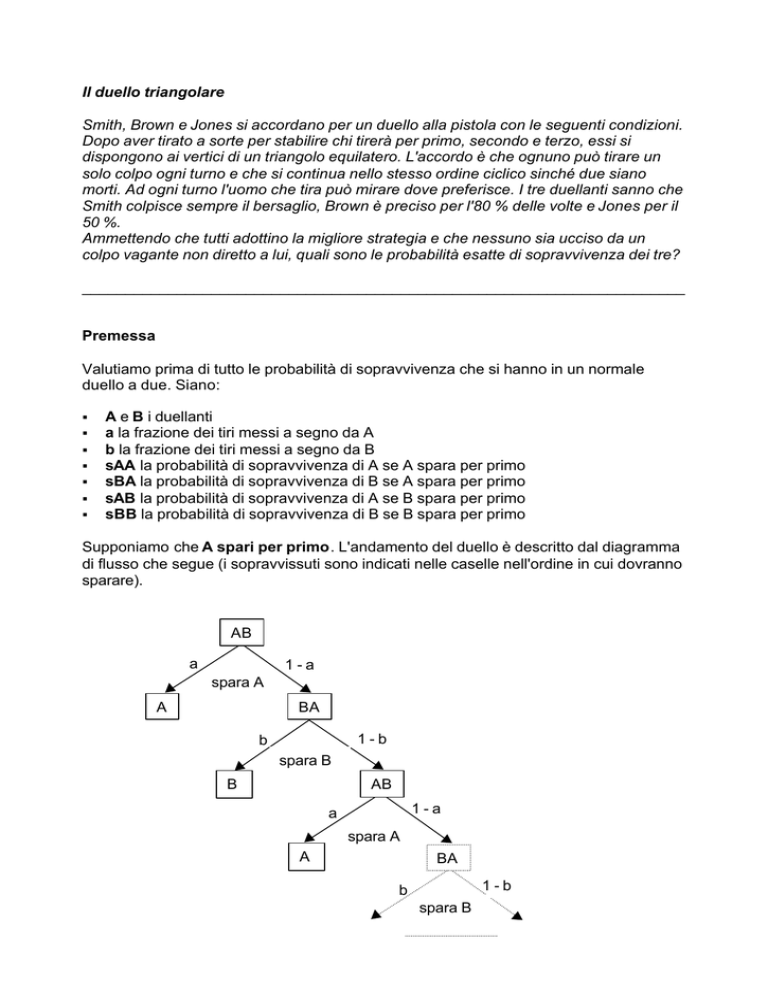
A e B i duellanti
a la frazione dei tiri messi a segno da A
b la frazione dei tiri messi a segno da B
sAA la probabilità di sopravvivenza di A se A spara per primo
sBA la probabilità di sopravvivenza di B se A spara per primo
sAB la probabilità di sopravvivenza di A se B spara per primo
sBB la probabilità di sopravvivenza di B se B spara per primo
Supponiamo che A spari per primo. L'andamento del duello è descritto dal diagramma
di flusso che segue (i sopravvissuti sono indicati nelle caselle nell'ordine in cui dovranno
sparare).
AB
a
1-a
spara A
A
BA
1-b
b
spara B
B
AB
1-a
a
spara A
A
BA
1-b
b
spara B
Dal diagramma si ricava
(1)
sAA = a + a(1-a)(1-b) +a(1-a)2 (1-b)2+....+ a(1-a)k(1-b)k + … = a / (a + b - ab)
(2)
sBA = 1 - sAA = (b - ab) / (a + b - ab)
Analogamente, se è invece B a sparare per primo
(3)
sAB = (a - ab ) / (a + b - ab)
(4)
sBB = 1 - sAB = b / (a + b - ab)
Strategia
La strategia ottimale seguita da ciascun duellante è quella di sparare all'avversario più
bravo. Solo così infatti, se il colpo è messo a segno, sarà massimizzata la probabilità di
sopravvivenza nel duello a due che seguirà.
Svolgimento del duello
In seguito abbreviamo con le iniziali i duellanti Smith, Brown e Jones.
Applicando le formule da (1) a (4) al problema proposto le probabilità di sopravvivenza
nei tre possibili duelli sono le seguenti:
Duellanti S e B
sSS = 1
sSB = 1/5
sBS = 4/5
sBB = 0
Duellanti S e J
sSS = 1
sSJ = 1/2
sJS = 0
sJJ = 1/2
Duellanti B e J
sBB = 8/9
sBJ = 5/9
sJB = 1/9
sJJ = 4/9
Esaminiamo ora l'andamento del duello triangolare.
Ordine di fuoco n° 1 SBJ oppure n° 2 SJB
I diagrammi di flusso sono rappresentati in figura e le probabilità di sopravvivenza
(l'ordine di fuoco è indicato in pedice) sono
sS1 = 1/2
sB1 = 0
sJ1 = 1/2
sS2 = 1/2
sB2 = 0
sJ S2 = 1/2
SBJ
SJB
1
spara S
JS
1/2
1
spara S
JS
1/2
1/2
spara J
J
sp
S
1/2
spara J
J
sp
Ordine di fuoco SBJ
S
Ordine di fuoco SJB
Ordine di fuoco n° 3 BSJ
Il diagramma di flusso è rappresentato in figura e le probabilità di sopravvivenza sono
sS3 = (1/5)(1/2) = 1/10
sB3 = (4/5)(4/9) = 16/45
sJ3 = (4/5)(5/9) + (1/5)(1/2 ) = 49/90
BSJ
4/5
1/5
spara B
JB
5/9
SBJ
4/9
spara S 1
spara J
J
sp
JS
B
1/2
1/2
spara J
J
sp
Ordine di fuoco BSJ
S
Ordine di fuoco n° 4 BJS
Il diagramma di flusso è rappresentato in figura e le probabilità di sopravvivenza sono
sS4 = (1/5)(1/2)(1/2) = 1/20
sB4 = (4/5)(4/9) + (1/5)(1/2)(8/9) = 4/9
sJ4 = (4/5)(5/9) + (1/5)(1/2)(1/9) + (1/5)(1/2)(1/2) = 91/180
BJS
4/5
1/5
spara B
JB
5/9
JSB
4/9
1/2
B
BJ
spara J
J
sp
8/9
1/2
spara J
SBJ
1/9
1
spara S
spara B
B
sp
J
JS
1/2
1/2
spara J
J
sp
S
Ordine di fuoco BJS
Ordine di fuoco n° 5 JSB
Il diagramma di flusso è rappresentato in figura e le probabilità di sopravvivenza sono
sS5 = (1/2)(1/2) = 1/4
sB5 = (1/2)(8/9) = 4/9
sJ5 = (1/2)(1/9) + (1/2)(1/2) = 11/36
JSB
1/2
1/2
spara J
BJ
SBJ
8/9
1/9
spara S 1
spara B
B
sp
JS
J
1/2
spara J
J
1/2
S
Ordine di fuoco JSB
Ordine di fuoco n° 6 JBS
Il diagramma di flusso è rappresentato in figura e le probabilità di sopravvivenza sono
sS6 = (1/2)(1/5)(1/2) = 1/20
sB6 = (1/2)(8/9) + (1/2)(4/5)(4/9) = 28/45
sJ6 = (1/2)(1/9) + (1/2)(4/5)(5/9) + (1/2)(1/5)(1/2) = 59 /180
JBS
1/2
1/2
spara J
BJ
8/9
BSJ
1/9
4/5
J
JB
spara B
B
sp
4/9
1/5
spara B
SBJ
5/9
1
spara S
spara J
B
ar
J
JS
1/2
1/2
spara J
J
sp
Ordine di fuoco JSB
S
Conclusioni
Poiché i sei ordini di fuoco sono equiprobabili (probabilità = 1/6), le probabilità di
sopravvivenza complessive sono date da
(5)
sS = (sS1 + sS2 + sS3+ sS4 + sS5 + sS6) / 6
(6)
sB = (sB1 + sB2 + sB3 + sB4 + sB5 + sB6 ) / 6
(7)
sJ = (sJ1 + sJ2 + sJ3+ sJ4+ sJ5 + sJ6 ) / 6
Sostituendo i valori numerici calcolati si hanno le probabilità richieste
sS = 29 / 120 = 0,24166
sB = 14 / 45 = 0,31111
sJ = 161/360 = 0,44722
Osservazioni
Per le date frazioni di tiri messi a segno dai duellanti Jones ha la probabilità più alta di
sopravvivere, benché sia il meno abile. La minore abilità di Jones è in questo caso più
che compensata dalla strategia adottata che spinge i duellanti a sparare al più bravo.
Se le frazioni dei tiri messi a segno dai duellanti fossero diverse si avrebbero casi in cui
la strategia di gara non riesce a sovvertire la scala di bravura. Ad esempio se Jones
mettesse a segno solo il 30 % dei tiri, a parità di tutto il resto si avrebbe
sS = 0,3706
sB = 0,3367
sJ = 0,2926