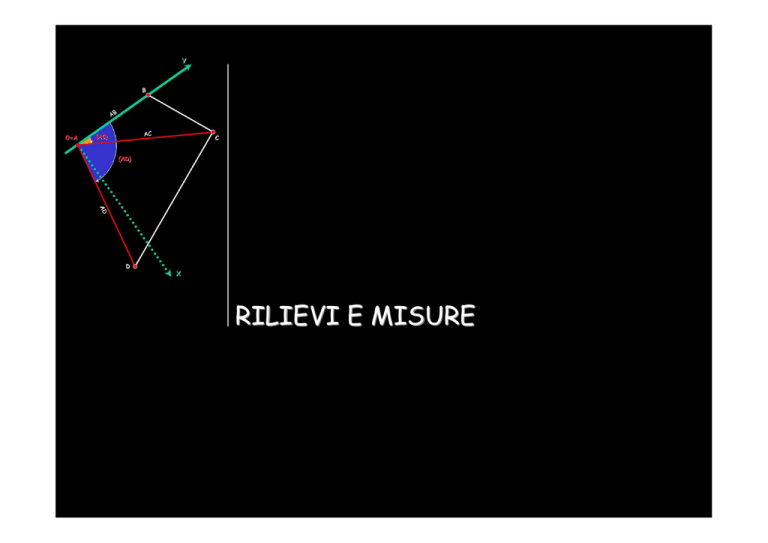
RILIEVI E MISURE
Topografia e rilievi topografici
Misure di angoli e distanze
Sistemi di riferimento
I rilievi planimetrici di dettaglio
. Coordinate polari
Indice
. Poligonali aperte
. Trilaterazioni
. Coordinate cartesiane
. Allineamenti
Conclusioni
La topografia (il cui termine derivante dal greco è composto da
topos = luogo e graphos = grafia) è la tecnica che ha per oggetto lo
Topografia
studio dei metodi, dei procedimenti applicativi, dei modelli di calcolo
e delle strumentazioni finalizzate al rilievo di una porzione limitata
della superficie fisica della Terra, sufficientemente piccola da
poterne trascurare la sfericità o curvatura
Prof. Ristorini
Si definisce rilievo topografico l’insieme delle operazioni con il
quale si determinano, partendo da misure angolari e lineari prese
Rilievo topografico
sul terreno, gli elementi necessari per eseguire la restituzione in
scala dell’oggetto rilevato. I rilievi topografici possono essere
planimetrici, altimetrici o completi (plano altimetrici)
I metodi di rilievo planimetrico consentono di individuare la posizione
del punto proiezione P’ sulla superficie di riferimento adottata,
mediante le coordinate X e Y, calcolate partendo dalle misure
Rilievo topografico
effettuate sul terreno.
I metodi di rilievo altimetrico permettono di conoscere la distanza
(coordinata Z o quota Q) del punto reale P dalla superficie di
riferimento
z
P (x ; y ; z)
punto reale
y
zp = Qp = quota
yp
xp
Rilievo topografico
o
(OP)
P ’ (x ; y) punto proiezione
D
π
x
XP = D x sen (OP)
YP = D x cos (OP)
I punti necessari a definire una rappresentazione
cartografica, che costituisce lo scopo primario di un
rilievo topografico, possono essere distinti in due
categorie:
Rilievo topografico
Differenze tra i
punti rilevati
punti di inquadramento o di appoggio
punti di dettaglio
I punti di inquadramento o di appoggio, di coordinate note,
formano una rete (di inquadramento) che costituisce la
struttura
Rilievi topografici
Punti di
inquadramento
portante
delle
successive
fasi
di
rilievo.
Generalmente i punti di appoggio sono in numero abbastanza
limitato,
omogeneamente distribuiti su tutta la zona da
rilevare. Sono posizionati in modo tale da consentirne una
buona visibilità e l’accessibilità per eseguire le misure.
Rilievi topografici
Rete di
inquadramento
I punti di dettaglio sono quelli ritenuti necessari per fornire una
corretta descrizione di tutti i particolari morfologici della zona
rilevata.
La posizione dei punti di dettaglio, che costituiscono la grande
Rilievi topografici
Punti di dettaglio
maggioranza dei punti rilevati, si ottiene collegandoli con misure
angolari o lineari ad uno o più punti della rete di inquadramento
Le operazioni di rilievo e successivo calcolo delle coordinate dei punti
di dettaglio sono molto più semplici di quelle impiegate per il rilievo dei
punti di appoggio
Y
(MC)
M
C
Rilievi topografici
rilievo di dettaglio
9
(AM)
Punti di appoggio e
8
XA
A
10
B
YA
(CM)
Il punto sul quale viene messo lo strumento si
chiama punto di stazione. La sua materializzazione
può essere costituita da una borchia metallica
infissa nella pavimentazione
stradale, da una
borchia cementata in un piccolo pilastrino in
cemento
armato,
oppure
da
un
punto
non
materializzato ma ben individuabile, come ad
Rilievi topografici
Materializzazione
dei punti
esempio l’incrocio di due assi stradali o l’angolo di
una tessera di un pavimento.
I punti battuti dalla stazione possono essere
individuati in vari modi; - da elementi artificiali o
naturali (punta di un campanile, spigolo di una
finestra, ...; da elementi metallici o picchetti che
vengono resi visibili da lontano con opportuni segnali
quali paline, prismi riflettenti, ...
La scelta dei punti da rilevare viene fatta dopo aver eseguito
una attenta ricognizione sul territorio. Dei punti scelti viene
redatta una apposita monografia corredata da schizzo
grafico o fotografia
Rilievo topografico
Identificazione dei
punti
I punti devono essere successivamente identificati. La scelta
più semplice è quella di tipo numerico con andamento
progressivo, ma può essere convenientemente adottata solo
per pochi punti. In caso contrario, pur mantenendosi una
numerazione progressiva questa è collegata al nome della
stazione da cui i punti sono stati rilevati. Il nome della
stazione è sempre multiplo di 100
ELEMENTI NATURALI
idrografia
vegetazione
morfologia
Rilievo topografico
Natura degli
elementi da rilevare
ELEMENTI ARTIFICIALI
rete viaria
insediamenti urbani
reti tecnologiche
confini
Le esigenze di precisione del rilievo dipendono dalla scala di
rappresentazione grafica e dall'errore di graficismo.
Generalmente l'errore ammesso nel disegno cartografico può
arrivare a 0.02 cm, per cui, chiamato D il denominatore di scala
Rilievi topografici
Precisione di un
della mappa, l'errore ammissibile nella conoscenza delle
coordinate di un punto è dato dalla:
rilievo
e = 0.02 D (cm)
ad esempio: se la mappa topografica ha un rapporto di scala
1:2000, e varrà 40 cm.
1 : 25000
1 : 10000
1 : 5000
Rilievo topografico
Scale di
rappresentazione
grafica
I particolari visibili sulla carta, che vanno quindi rilevati, sono da mettere in
relazione con la scala di rappresentazione e con gli scopi per cui viene
realizzata la carta stessa
In effetti più grande è la scala della carta, maggiore sarà la sua definizione
e di conseguenza maggiori saranno i particolari che dovranno essere rilevati
SCALA
Rilievo topografico
Scale di
rappresentazione
CARTA
REALTA’
1 : 100
100 cm
1 m
1 : 1000
1000 cm
10 m
1 : 2000
2000 cm
20 m
5000 cm
50 m
1 : 10000
10000 cm
100 m
1 : 25000
25000 cm
250 m
grafica
1 : 5000
1 cm
L’organizzazione di un rilievo si compone delle seguenti fasi:
raccolta delle informazioni
ricognizione
Rilievo topografico
Fasi
progetto
esecuzione
elaborazione dei dati
restituzione grafica
collaudo
0c
A
(OA)
O
Misura di angoli e
distanze
(OB)
AÔB = (OB) - (OA)
(OC)
B
BÔC = (OC) - (OB)
C
angoli orizzontali per differenza di letture
0c
O
A
AÔB
0c
Misura di angoli e
distanze
BÔC
B
C
angoli orizzontali per letture isolate
0c = 400c
A
B
BŜA
(SB)
Misura di angoli e
distanze
(SA)
S
Attenzione
AŜB = (SB) – (SA)
ma
BŜA = [400c – (SB)] + (SA)
Angolo verticale o zenitale
È l’angolo φ compreso tra la verticale e la direzione considerata.
Alternativamente è possibile utilizzare l’angolo α di elevazione, cioè quello
che si forma tra l’orizzontale e il punto considerato
do = dr x sen φ
dr
φ
Misura di angoli e
distanze
x
α
h
B
x
A
do
x
Eseguito il rilievo è possibile determinare le coordinate cartesiane dei
punti rilevati, con cui successivamente si esegue il disegno nella scala
desiderata. Per il calcolo delle coordinate è necessario adottare un
Sistemi di
riferimento locali
sistema
di
riferimento
cartesiano
(scegliere
cioè
l’origine
e
l’orientamento degli assi). Nel caso di sistemi di riferimento locali,
collegati al rilievo eseguito, la scelta da effettuare deve essere tale
che, la successiva esecuzione dei calcoli, sia la più semplice e rapida
possibile
I metodi di rilievo planimetrico utilizzati nella tecnica
professionale
sono
numerosi.
Tuttavia
l’evoluzione
della
tecnologia ha determinato una decisa selezione a seguito della
quale pochi di questi trovano effettivo impiego pratico
I rilievi planimetrici
In effetti tra i metodi che utilizzano tecnologie tradizionali, di
fatto il metodo quasi esclusivamente impiegato nel rilievo dei
particolari, per la rapidità e la semplicità operativa, è quello per
coordinate polari (o irradiamento). Con esso, di ciascun punto
rilevato vengono misurate, dalla stazione di partenza la
distanza e la direzione (azimut o angolo al vertice)
I rilievi planimetrici
Schemi geometrici
RILIEVO PER COORDINATE POLARI
RILIEVO PER POLIGONAZIONE
RILIEVO PER TRILATERAZIONE
RILIEVO PER COORDINATE CARTESIANE
L’appezzamento
ABCD
0c
viene
rilevato dal punto di stazione
A, da cui risultano visibili
B
gli
AB
altri punti. Orientato lo zero
del
cerchio
orizzontale
si
AC
(AC)
A
(AD)
Rilievo per
coordinate polari
misurano distanze e azimut
AD
Libretto delle Misure
Staz.
Punti
Angoli
Distanze
B
0c.0000
32.150
D
A
C
30c.1580
48.160
D
108c.6250
52.130
C
Il
sistema
conveniente
di
per
riferimento
il
calcolo
Y
più
delle
B
AB
coordinate cartesiane dei punti è
Rilievo per
coordinate polari
Calcolo delle
coordinate
cartesiane
quello che fa coincidere l’origine con la
O=A
AC
(AC)
C
(AD)
stazione A e il semiasse positivo delle
Y con il lato AB. In questo modo
AD
risultano note le coordinate del punto
A (Xa = 0 m; Ya = 0 m), le coordinate
del punto B (Xb = 0 m; Yb = AB)
D
X
N (0c)
asse polare
Y
A’
YA
XA
(OA)
A
A
O
Rilievo per
coordinate polari
Calcolo delle
coordinate
cartesiane
Ti ricordo che .......
O (polo)
X
...... il passaggio diretto da polari a cartesiane è possibile solo se:
le origini dei due sistemi coincidono
il semiasse positivo delle Y coincide con l’asse polare.
Si utilizzano le formule
XA = OA x sen (OA)
YA = OA x cos (OA)
XA = 0 m
Y
YA = 0 m
B
XB = 0 m
AB
YB = AB
O=A
Rilievo per
coordinate polari
Calcolo delle
coordinate
cartesiane
AC
(AC)
C
XC = AC x sen (AC)
(AD)
YC = AC x cos (AC)
XD = AD x sen (AD)
Note le coordinate dei punti è possibile
calcolare tutti gli altri elementi
inicogniti, come distanze, azimut e area
dell’appezzamento
AD
YD = AD x cos (AD)
D
X
Libretto delle Misure
Staz.
Punti
Angoli
Distanze
B
0c.0000
32.150
C
30c.1580
48.160
D
103c.6250
52.130
Y
B
A
AB
O=A
AC
(AC)
C
XA = 0 m
Rilievo per
coordinate polari
YA = 0 m
Esempio di calcolo
coordinate
cartesiane
XB = 0 m
(AD)
YB = AB = 32.150 m
AD
XC = AC x sen (AC) = 48.160 x sen 30c.1580 = 21.970 m
YC = AC x cos (AC) = 48.160 x cos 30c.1580 = 42.856 m
XD = AD x sen (AD) = 52.130x sen 103c.6250 = 52.045 m
YD = AD x cos (AD) = 52.130 x cos 103c.6250 = - 2.966 m
D
X
Oc
A
S
D
B
Rilievo per
coordinate polari
Altri schemi
Libretto delle Misure
C
Staz.
S
Punti
Angoli
Distanze
A
30c.2500
44.150
B
110c.8100
40.620
C
212c.1600
38.220
D
302c.6200
33.130
Y
A
XS = 0 m
XS = 0 m
XA = SA x sen (SA) = 44.15 x sen 30c.25 = 20.352 m
YA = SA x cos (SA) = 44.15 x cos 30c.25 = 30.258 m
D
X
O=S
B
Rilievo per
coordinate polari
XB = SB x sen (SB) = 40.62 x sen 110c.81 = 40.035 m
YB = SB x cos (SB) = 40.62 x cos 110c.81 = - 6.864 m
Altri schemi
XC = SC x sen (SC) = 38.22 x sen 212c.16 = - 7.256 m
YC = SC x cos (SC) = 38.22 x cos 212c.16 = - 37.524 m
C
XD = SD x sen (SD) = 33.13 x sen 302c.62 = ...
Libretto delle Misure
Staz.
S
Punti
Angoli
Distanze
A
30c.2500
44.150
B
110c.8100
40.620
C
212c.1600
38.220
D
302c.6200
33.130
YD = SD x cos (SD) = 52.13 x cos 302c.62 = ...
Le poligonali aperte sono costituite da una
spezzata di cui si misurano tutte le distanze e gli
E
angoli nei vertici
D̂
Ĉ
C
B̂
Poligonali aperte
A
STAZ.
B
C
D
B
PUNTI
C.O.
DIST.
A
0c.0000
59.620
C
122c.3650
42.130
B
0c.0000
------
D
239c.1830
40.900
C
0c.0000
------
E
67c.1550
51.250
D
Il sistema di riferimento più conveniente per il calcolo delle coordinate
cartesiane dei punti della poligonale è quello che fa coincidere l’origine con il
primo punto A e il semiasse positivo delle X con il primo lato AB. Con questa
scelta risultano note le coordinate del punto A (Xa = 0 m; Ya = 0 m), le
coordinate del punto B (Xb = AB; Yb = 0 m) e l’azimut (AB) = 100c
Poligonali aperte
Y
Calcolo delle
coordinate
cartesiane
Scelta del sistema
di riferimento
E
D̂
Ĉ
D
C
(AB) = 100c
B̂
O=A
B
X
Y
E
D̂
Ĉ
XC
D
C
Poligonali aperte
Calcolo delle
coordinate dei
punti successivi
YC
(AB) = 100c
(BC)
B̂
O=A
B
X
Per il calcolo delle coordinate del punto C rispetto al sistema con origine in A si
opera come segue: - si sposta il semiasse positivo delle Y nel punto B che
precede il punto C; - si calcola l’azimut (BC) utilizzando la formula di
propagazione: “l’azimut (BC) si ottiene sommando all’azimut precedente (AB)
l’angolo nel vertice B. Se tale somma è maggiore di 200c, si sottrae un angolo
piatto. Se invece è inferiore a 200c si somma un angolo piatto”
(BC) = (AB) + B ± 200c
Y
XC = XB + C’C
C’
YC
C
(BC)
(AB) = 100c
B̂
O=A
XB
B
X
Poligonali aperte
Calcolo delle
coordinate dei
punti successivi
Le coordinate di C si calcolano risolvendo il triangolo rettangolo BC’C di cui si
conoscono l’ipotenusa BC perchè misurata durante il rilievo e l’azimut (BC)
calcolato con la formula di propagazione. I due cateti incogniti, che
rappresentano le “coordinate parziali del punto C rispetto al sistema posto nel
vertice B”, si calcolano con:
C’C = BC x sen (BC)
BC’ = BC x cos (BC)
Y
XC = XB + C’C
C’
YC
C
(BC)
100c
(AB) = 100
B̂
XB
O=A
B
X
Poligonali aperte
Calcolo delle
coordinate dei
punti successivi
Sommando alle coordinate parziali C’C e BC’ le coordinate del punto precedente
B note, si ottengono le “coordinate totali del punto C rispetto al sistema
cartesiano con origine in A”:
XC = XB + CC’ = XB + BC x sen (BC)
YC = YB + BC’ = YB + BC x cos (BC)
Y
E
(CD)
Ĉ
XC
C
Poligonali aperte
Calcolo delle
coordinate dei
punti successivi
YC
(AB) = 100c
(DE)
(BC)
B̂
O=A
D
B
X
Per i punti successivi D, E, ...... si procede come per il punto C.
Si calcolano tutti gli azimut con la formula di propagazione
(CD) = (BC) + C ± 200c
(DE) = (CD) + D ± 200c
Y
Xe
E
Xd
(CD)
Ĉ
XC
C
Poligonali aperte
Calcolo delle
coordinate dei
punti successivi
YC
(AB) = 100c
(DE)
(BC)
B̂
O=A
D
B
X
Noti gli azimut si calcolano le coordinate totali dei punti sommando alle
coordinate totali del punto precedente le coordinate parziali tra i due punti
considerati
XD = XC + CD x sen (CD)
YD = YC + CD x cos (CD)
XE = XD + DE x sen (DE)
YE = YD + DE x cos (DE)
Y
E
(EA)
(ED)
AE
D
C
(AE)
Poligonali aperte
Note le coordinate
dei punti, possono
essere calcolati
..........
(AB) = 100c
A
B
X
distanza AE = √ (XE2 + YE2)
azimut (AE) = tg-1 (XE / YE)
angolo A = (AB) – (AE)
superficie S = 0.5 x [ YA x (XB – XE) + YB x (XC – XA) + ....]
Calcolo degli azimut
Y
(AB) = 100c
Xe
(BC) = (AB) + B ± 200c = 22c.3650
E
(CD) = (BC) + C ± 200c = 61c.5480
(DE) = (CD) + D ± 200c = 328c.7030
E
A
Calcolo delle coordinate dei punti
(CD)
Ye
Ĉ
XA = 0 m
Poligonali aperte
Esempio di calcolo
XB = AB = 59.620 m
(DE)
C
(AE)
YA = 0 m
(AB) = 100c
B̂
(BC)
X
O=A
B
YB = 0 m
XC = XB + BC x sen (BC) = 74.118 m
YC = YB + BC x cos (BC) = 39.556 m
XD = XC + CD x sen (CD) = 107.781 m
STAZ
YD = YC + CD x cos (CD) = 62.784 m
XE = XD + DE x sen (DE) = 61.652 m
PUNTI
C.O.
DIST.
A
0c.0000
59.620
C
122c.3650
42.130
B
0c.0000
------
D
239c.1830
40.900
C
0c.0000
------
E
67c.1550
51.250
B
YE = YD + DE x cos (DE) = 85.115 m
C
Distanza AE e Azimut (AE)
AE = √ (XE2 + YE2) = 105.097 m
(AE) = tg-1 (XE/YE) = 39c.9080
D
D
Stabiliti sul terreno i punti da rilevare si collegano tra loro con una rete di
triangoli di cui si misurano tutti i lati. Il numero delle misure effettuate deve
essere sovrabbondante rispetto a quelle strettamente necessarie, perchè le
misure in più permettono di effettuare verifiche. La restituzione in scala si
Rilievo per
trilaterazioni
realizza dall’intersezione di due archi di circonferenza, convergenti sul punto
da individuare, il cui raggio rappresenta in scala la distanza tra i punti. I
rilievi per trilaterazioni sono molto utilizzati per la realizzazione di rilievi di
interni sia in campo archeologico che architettonico
C
D
RILIEVO
A
B
Rilievo per
trilaterazioni
C
D
RESTITUZIONE
A
B
I punti da rilevare sono riferiti ad un allineamento principale
che si assume come asse delle ascisse e su di esso si sceglie
opportunamente l’origine. Determinati con uno squadro i piedi
delle
perpendicolari
principale,
Rilievo per
coordinate
cartesiane
si
condotte
misurano
le
dai
punti
lunghezze
all’allineamento
degli
allineamenti
secondari e le loro distanze dall’origine ottenendo così per
ogni punto una coppia di ascisse e ordinate. Con questo tipo di
rilievo possono commettersi errori nella determinazione delle:
distanze
perpendicolari
2
1
+
A
5
3
B
+
4
Rilievo per
coordinate
cartesiane
PUNTI
X
Y
A
0.000
0.000
1
- 13.250
+ 22.160
2
- 28. 200
+ 22.160
3
+ 7.510
+ 29.400
4
+ 28.120
+ 29.400
5
...
...
...
...
...
B
0.000
+ 60.000
Con il termine allineamento si intende la linea di intersezione
con terreno di un piano verticale passante per due punti
assegnati. La materializzazione sul terreno di un allineamento
può essere fatta utilizzando un sufficiente numero di paline
disposte in modo da essere contenute nell’ideale piano verticale
Allineamenti
passante per i due punti estremi. Nella realizzare l’allineamento
si deve avere l’accortezza di cominciare dalla palina più lontana;
infatti, se si procedesse al contrario, partendo da quella più
vicina all’osservatore, la prima palina posta coprirebbe le
successive anche se queste non fossero ben allineate
A
3
2
Lo squadro è uno strumento semplice
che consente di individuare direzioni
Allineamenti
Squadri
formanti tra loro un angolo voluto. È
composto da un corpo cilindrico, sferico
o prismatico a base esagonale, sulle cui
superfici esterne sono praticate, in
posizione diametralmente opposta, delle
fessure che formano angoli di 45° e
90°.
1
B
Spostandosi sull’allineamento dato (r) si determina la proiezione P’ piede
della perpendicolare condatta da P su r. Si misura la distanza PP’. Da un
secondo punto S’, posto su r, si traccia l’allineamento perpendicolare e si
riporta la distanza SS’ = PP’. L’allineamento PS è così determinato.
Problemi sugli
allineamenti
Per un punto P
tracciare
l’allineamento PS
parallelo ad r
P
PP’
r
P’
S
SS’
S’
Sia AB l’allineamento da prolungare oltre l’ostacolo. Con uno squadro si
traccia l’allineamento EF parallelo ad AB posto a distanza nota. Sul
prolungamento di EF si scelgono due punti G e H e si tracciano due
allineamenti perpendicolari. Riportando la distanza nota, si ottengono i
due punti C e D che individuano il prolungamento di AB
Problemi sugli
allineamenti
Prolungamento di un
allineamento oltre
un ostacolo
B
A
C
d
d
E
D
d
F
G
d
H
L’esempio preso in considerazione riguarda l’inserimento di un fabbricato di
nuova costruzione in una particella di terreno. La posizione dei vertici del
fabbricato è individuata tramite allineamenti secondari (evidenziati in rosso),
che intersecano gli allineamenti principali, costituiti dal confine della particella.
Sugli allineamenti principali sono prese le misure necessarie per la successiva
restituzione grafica
Rilievi per
allineamenti
PF17
... in uno stesso rilievo possono
100
essere utilizzati, se necessario,
200
PARTICOLARE
schemi geometrici differenti
500
600
700
300
Conclusioni
400
È bene chiarire
che ...
PF02
PF11
2
1
+
600
5
3
+
4
700