problemi sulla media

Problemi sui test di ipotesi per la media
Problema M1
Un costruttore produce un modello di lampada che ha una vita tipica di 1600 ore.
Sulla popolazione (infinita) di tali lampade si può definire una variabile causale X che assume, per
ciascun esemplare, valore uguale alla vita espressa in ore. Dai dati storici della produzione si è
individuato che la variabile X presenta, per l'intera popolazione, un valore della media pari a 1600
ed un valore della deviazione standard pari a 120.
µ = 1600 ;
σ = 120
Il costruttore vuole verificare se l’invecchiamento della linea di produzione possa aver determinato
una variazione della media di tale variabile X tale da rendere necessaria una manutenzione
straordinaria dei macchinari. Si considera negativa sia la diminuzione della media (minore
qualità), sia l’aumento della media (minore turn-over delle lampade già installate con conseguente
riduzione del mercato). Si vuole condurre il test con una fiducia del 96% (α = 4%).
Allo scopo viene prelevato un campione di 100 lampade da cui si determina il valore della media
campionaria che risulta pari a 1570.
L’ipotesi principale che viene assunta è:
H0 : µ = µ0 = 1600
ed il test viene svolto con la statistica campionaria Z:
Z=
X n − µ0
σ
n
che presenta una distribuzione di tipo "normale standardizzata".
I valori della X ricavati dal campione di 100 elementi portano a:
X n = 1570
Dato che l'ipotesi è del tipo "µ = µ0" si esegue un test di tipo "bilaterale" (o "a 2 code")
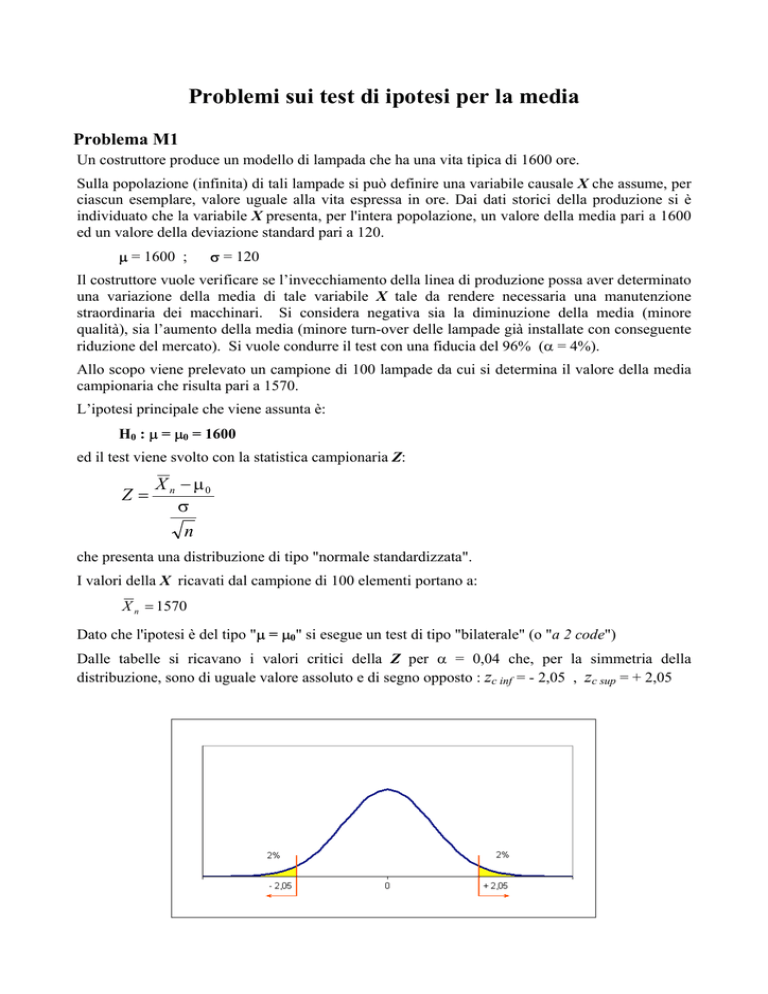
Dalle tabelle si ricavano i valori critici della Z per α = 0,04 che, per la simmetria della
distribuzione, sono di uguale valore assoluto e di segno opposto : zc inf = - 2,05 , zc sup = + 2,05
La regione di rifiuto della H0 è pertanto:
Z < zc inf oppure
Z > zc sup
Determiniamo il valore della Z corrispondente ai dati del campione ricavando:
Z=
X n − µ0
1570 − 1600
⇒ zn =
= − 2,5
σ
120
10
n
Dato che zn cade nella regione di rifiuto inferiore Z < zc
richiesta:
inf
posso rifiutare H0 con la fiducia
la media della variabile X per l'intera popolazione non è uguale a 1600.
Come conseguenza del rifiuto eseguito è possibile sostenere che la vita tipica delle lampade
prodotte non è più di 1600 ore.
Se si fosse richiesta una fiducia del 99% (α = 1%) nel rifiuto di H0 si sarebbero trovati i valori
critici
zc inf = - 2,58 ; zc sup = + 2,58
Dal campione si è ricavato un valore di zn = -2,5 che sarebbe rimasto nella regione di non rifiuto di
H0, pertanto non sarebbe stato possibile rifiutare H0 con la fiducia richiesta ed il test non avrebbe
dato risultati utili.
Problema M2
Il costruttore del problema precedente garantisce che le lampade da lui prodotte hanno una vita
tipica superiore a 1570 ore. Un importante cliente ritiene che ciò non sia vero e richiede al
costruttore una verifica.
Il costruttore preleva un campione di 100 lampade e organizza un test per convincere il cliente che
le sue supposizioni sono prive di fondamento.
Sulla popolazione (infinita) delle lampade si definisce anche in questo caso una variabile causale X
che assume, per ciascun esemplare, valore uguale alla vita espressa in ore.
Dai dati storici della produzione si è individuato che la variabile X presenta una deviazione
standard per l'intera popolazione σ = 120.
L'ipotesi principale che viene sottoposta al test è:
H0 : µ < µ0 = 1570
ed il test viene svolto, con una fiducia richiesta del 95%, utilizzando la statistica campionaria Z:
Z=
X n − µ0
σ
n
che presenta una distribuzione di tipo "normale standardizzata".
I valori della X ricavati dal campione di 100 elementi portano a:
X n = 1591
Dato che l'ipotesi è del tipo "µ < µ0" si esegue un test di tipo "unilaterale" (o "a 1 coda")
Dalle tabelle si ricava il valore critico della Z per α = 0,05: zc sup = + 1,645
La regione di rifiuto della H0 è pertanto:
Z > zc sup
Determiniamo il valore della Z corrispondente ai dati del campione ricavando:
Z=
X n − µ0
1591 − 1570
⇒ zn =
= + 1,75
σ
120
10
n
Dato che zn cade nella regione di rifiuto Z > zc sup posso rifiutare H0 con la fiducia richiesta:
la media della variabile X per l'intera popolazione non è minore o uguale a 1570.
Il risultato del test mostra al cliente che i suoi dubbi sulla qualità delle lampade prodotte non sono
plausibili, e lo fa con una fiducia del 95%.
Problema M3
Un costruttore afferma che le funi in acciaio di sua produzione hanno un carico di rottura non
inferiore a 8000 N, ma un cliente teme che tale valore sia ottimistico e decide di acquistare una
campionatura con cui verificare personalmente l’affermazione del costruttore con una fiducia del
95% per il test.
Sulla popolazione (infinita) delle funi si definisce una variabile causale X che assume, per ciascun
esemplare, valore uguale al carico di rottura espresso in newton ( N ).
L'ipotesi principale che viene sottoposta al test è:
H0 : µ ≥ µ0 = 8000
Si acquistano 6 funi e si determinano la media campionaria e la varianza campionaria corretta:
X n = 7750 ; S n2 = 21025 ⇒ S n = 145
Dato che il campione è di soli 6 elementi il test viene condotto con la fiducia richiesta del 95%,
utilizzando la statistica campionaria T:
T=
X n − µ0
Sn
n
che presenta una distribuzione di tipo "t di Student".
Dato che l'ipotesi è del tipo "µ > µ0" si esegue un test di
tipo "unilaterale" (o "a 1 coda")
Il campione ha n = 6 pertanto si usa la t di Student con 5
gradi di libertà: dalle tabelle si ricava il valore critico della
T per α = 0,05 che risulta: tc inf = - 2,015
La regione di rifiuto della H0 è pertanto:
T < tc inf
Dai dati del campione si ricava:
T=
X n − µ0
7750 − 8000
⇒ tn =
= − 4,22
Sn
145
6
n
Dato che tn cade nella regione di rifiuto T < tc inf posso rifiutare H0 con la fiducia richiesta:
la media della variabile X per l'intera popolazione non è maggiore o uguale a 8000.
Come conseguenza del rifiuto di H0 si può sostenere, con il 95% di fiducia, che la affermazione del
costruttore sul fatto che il carico di rottura delle sue funi è non inferiore a 8000 newton non è
corretta.
Problema M4
Una cooperativa di tassisti vuole verificare il consumo urbano di un nuovo modello di vettura che
il costruttore afferma essere non superiore a 5 l/100km. Vengono acquistate 8 vetture e si procede
ad una sperimentazione che si vuole condurre, con un livello di fiducia del 99%, allo scopo di
evitare l’acquisto di un “bidone” che consuma più di quanto reclamizzato.
Si definisce una variabile casuale X che assume, per ciascun elemento della popolazione infinita
delle auto, valore uguale al valore del consumo urbano espresso in litri / 100 km.
In conseguenza dello scopo del test si definisce la seguente ipotesi principale:
H0 : µ ≤ µ0 = 5
Condotta la sperimentazione su strada si determinano la media campionaria e la varianza
campionaria corretta relative al consumo urbano delle vetture:
X n = 5,5
;
S n = 0,6
Dato che il campione è di soli 8 elementi il test viene condotto con la fiducia richiesta del 99%,
utilizzando la statistica campionaria T:
T=
X n − µ0
Sn
n
che presenta una distribuzione di tipo "t di Student".
Dato che l'ipotesi è del tipo "µ < µ0" si esegue un test di tipo "unilaterale" (o "a 1 coda")
Il campione ha n = 8 pertanto si usa la t di
Student con 7 gradi di libertà: dalle tabelle si
ricava il valore critico della T per α = 0,01 che
risulta: tc sup = 2,998 .
La regione di rifiuto della H0 è pertanto:
T > tc sup = 2,998
Dai dati del campione si è ricavato:
X n = 5,5
;
S n = 0,6
da cui si ottiene:
T=
X n − µ0
5,5 − 5
⇒ tn =
= + 2,35
Sn
0,6
8
n
Dato che tn NON cade nella regione di rifiuto T > tc sup = 2,998 il risultato del test non permette
di rifiutare H0 con la fiducia richiesta. Non si è pertanto autorizzati a scartare l’ipotesi secondo
cui il consumo delle vetture è non superiore a 5 l/100km.
Problema M5
Un costruttore di trasformatori deve acquistare del filo di rame per avvolgere le bobine da un
nuovo fornitore. Egli vuole verificare se il diametro tipico del filo è realmente di 1,54 mm pertanto
ordina una campionatura di 26 matasse per condurre, con una fiducia del 95%, un test “a due
code” in quanto intende scartare la eventuale fornitura sia per un diametro inferiore, sia per un
diametro superiore al pattuito.
Il costruttore di trasformatori definisce una variabile casuale X che assume, per ciascun elemento
della popolazione infinita delle matasse di filo, valore uguale al valore medio del diametro del filo
espresso in centesimi di millimetro e misurato in 5 punti distanti più di un metro l'uno dall'altro.
L'ipotesi principale che viene sottoposta al test è:
H0 : µ = µ0 = 154
Dato che non si conosce la varianza della X e che il campione è di 26 elementi il test viene
condotto con la fiducia richiesta del 95%, utilizzando la statistica campionaria T:
T=
X n − µ0
Sn
n
che presenta una distribuzione di tipo "t di Student".
Dato che l'ipotesi è del tipo "µ = µ0" si esegue un test di tipo "bilaterale" (o "a 2 code")
Il campione ha n = 26 pertanto si usa la t di Student con 25 gradi di libertà: dalle tabelle si ricavano
i due valori critici della T per α = 0,05 che risultano: tc inf = -2,060 e tc sup = 2,060
La regione di rifiuto della H0 è pertanto:
T < tc inf = -2,060 oppure
T > tc sup = 2,060
Dal campione si ricavano i seguenti valori:
X n = 160 ;
S n = 23
pertanto:
T=
X n − µ0
160 − 154
⇒ tn =
= 1,330
Sn
23
26
n
Dato che il valore della T non appartiene alla regione di rifiuto non è possibile rifiutare H0 con la
fiducia richiesta pertanto:
il costruttore di trasformatori non è autorizzato ad affermare che il diametro tipico del
filo sia diverso da 1,54 mm.
Problema M6
Un costruttore realizza una presa BNC, indicata come "Mod. A", che presenta un valore tipico
della perdita di 0,2 dB (a 3 GHz). Un campione di 30 prototipi realizzati con un procedimento
meno costoso, che indichiamo come "Mod. B", sembra evidenziare una perdita maggiore: è un
fatto accidentale oppure il nuovo processo porta a realizzare prodotti scadenti? Si desidera dare
una risposta con una fiducia del 95%.
Notiamo che i valori delle perdite sono espressi in dB, cioè in una scala non lineare. Poiché le
variabili casuali di cui abbiamo studiato le distribuzioni sono lineari è necessario operare una
linearizzazione della scala al momento in cui si definisce la variabile casuale con cui effettuare il
test:
Indicando con Vin e Vout rispettivamente il valore efficace del segnale in ingresso ed in uscita dalla
presa, il valore in dB della perdita della presa, che indichiamo PdB, viene definito come
PdB = 20 log10
Vin
Vout
Definiamo quindi una variabile casuale X che assume, per ciascuna presa, valore uguale al
rapporto fra Vin e Vout misurato a 3 GHz.
Dopo avere definito la variabile casuale X possiamo valutare il suo valore medio µA per la
popolazione delle prese "Mod. A" assumendo che esso coincida con il valore che corrisponde alla
perdita tipica di 0,2 dB ricavabile dai dati storici della produzione:
⎛ 0, 2 ⎞
⎜
⎟
V
V
PdB = 20 log10 in = 0,2 ⇒ in = 10⎝ 20 ⎠ = 1,023
Vout
Vout
da cui:
µA = 1,023
Il test verrà condotto allo scopo di verificare se il nuovo processo produttivo provoca un
aumento della perdita a 3 GHz rispetto a quella tipica del Mod. A.
La ipotesi principale che viene elaborata e sottoposta al test è la seguente:
H0 : µ < µ0 = 1,023
La fiducia richiesta al test è pari al 95% pertanto α = 0,05.
Dato che non si conosce la varianza della X il test viene condotto con la fiducia richiesta del 95%,
utilizzando la statistica campionaria T:
T=
X n − µ0
Sn
n
che presenta una distribuzione di tipo "t di Student". La elevata numerosità del campione (n = 30)
avrebbe permesso di approssimare la T con una distribuzione normale standardizzata, ma si è
preferito usare la soluzione rigorosa.
Dato che l'ipotesi è del tipo "µ < µ0" si esegue un test di tipo "unilaterale" (o "a 1 coda")
Il campione ha n = 30 pertanto si usa la t di Student con 29 gradi di libertà: dalle tabelle si ricava il
valore critico della T per α = 0,05 che risulta: tc sup = 1,699
La regione di rifiuto della H0 è pertanto:
T > tc sup = 1,699
Le misurazioni condotte sui 30 elementi "Mod. B" del campione hanno dato i seguenti risultati:
frequenza
Vin / Vout misurato a 3 GHz
3
1,025
7
1,030
10
1,035
7
1,040
3
1,045
Elaborando i dati emersi dalle misurazioni condotte sui prototipi "Mod. B" del campione si
ottengono i seguenti risultati:
1
Xn =
n
∑X
n
j
⇒
j =1
⇒ Xn =
3 ⋅1,025 + 7 ⋅1,030 + 10 ⋅1,035 + 7 ⋅1,040 + 3 ⋅1,025
= 1,035
30
1
S =
n −1
∑ (X
e
2
n
n
− Xn) ⇒
2
j
j =1
3 ⋅ (− 0,010 ) + 7 ⋅ (− 0,005) + 10 ⋅ (0 ) + 7 ⋅ (+ 0,005) + 3 ⋅ (+ 0,010 )
⇒ S =
=
29
0,00095
=
= 0,00003275
29
2
2
2
2
2
n
da cui:
S n = S n2 ⇒
⇒ S n = 0,00003275 = 0,0057
Dai dati del campione è quindi possibile esprimere anche la perdita
(media campionaria) della presa "Mod. B" in dB ottenendo:
PdB = 20 log10
Vin
⇒
Vout
⇒ PdB = 20 log10 1,035 ≈ 0,3 dB
2
Dal campione si sono ricavano i seguenti valori:
X n = 1,035 ;
S n = 0,0057
pertanto:
T=
X n − µ0
1,035 − 1,023
⇒ tn =
= + 11,5
0,0057
Sn
30
n
Dato che tn cade nella regione di rifiuto T > tc sup posso rifiutare H0 con la fiducia richiesta:
la media della variabile X per la popolazione futura "Mod. B"
non è minore o uguale a 1,023.
Come conseguenza del rifiuto di H0 si può sostenere, con il 95% di fiducia, che il nuovo processo
produttivo provoca una diminuzione della qualità del prodotto.
Il fatto che il campione dei 30 prototipi mostri una perdita di circa 0,3 dB non è dovuto alla
aleatorietà del campionamento, ma appare plausibile sostenere che è provocato da una sistematica
diminuzione delle qualità del prodotto.
_______________________________
Qualora si volesse individuare l’intervallo di confidenza al 95% per la perdita della presa BNC
Mod. B si opera nel seguente modo:
dalla tabella della t di Student con 29 gradi di libertà si individuano i due valori dei quantili che
lasciano il 2,5% in ciascuna delle due code: tQinf = − 2,045 e tQsup = + 2,045
Xn +
Sn
t Qinf ≤ µ ≤ X n +
Sn
t Qsup
n
n
0,0057
0,0057
1,035 +
⋅ (− 2,045) ≤ µ ≤ 1,035 +
⋅ (+ 2,045)
5,47
5,47
1,033 ≤ µ ≤ 1,037
da cui si ricavano le due espressioni equivalenti:
1,033 ≤ µ ≤ 1,037
e
0,28 dB ≤ µ ≤ 0,32 dB
Problema M7
Il signor Pinco Pallo, assemblatore di Personal Computer, deve acquistare una grande partita di
memorie RAM. Da riviste specializzate ha appreso che il costruttore delle memorie ha
recentemente migliorato il processo produttivo ed il valore tipico dell’assorbimento di corrente del
suo prodotto è passato da 50 mA a 45 mA. Pinco Pallo vuole assicurarsi che le RAM acquistate
siano della nuova serie e non “fondi di magazzino” pertanto organizza un test statistico su un
campione di 25 elementi.
Preliminarmente definisce una variabile casuale X che assume valori uguali alla intensità della
corrente assorbita dal chip di memoria misurata in mA.
Fissa un valore del rischio di prima specie α = 1% e accetta un rischio di errore di seconda specie
β ≤ 5% - In altri termini si può dire che fissa la fiducia del test al 99% e richiede una potenza
minima del 95% contro l’ipotesi alternativa.
Nella definizione della ipotesi principale e di quella alternativa Pinco Pallo opera con l'obiettivo di
poter ottenere informazioni utili ad evitare l'acquisto di un prodotto obsoleto: con quest'ottica
l'ipotesi principale, che si cerca di rifiutare, è quella per cui il valore tipico dell’assorbimento di
corrente è di 45 mA. Le ipotesi che Pinco Pallo elabora sono pertanto le seguenti:
H0 : µ ≤ µ0 = 45
α = 1%
H1 : µ = µ1 = 50
β ≤ 5%
Dal campione si ricavano sia la media campionaria sia la deviazione standard campionaria corretta
per la variabile casuale X:
X n = 48 ; S n2 = 25
⇒ Sn = 5
Dato che il campione è di 25 elementi e non è conosciuta la varianza σ2 il test viene condotto
mediante la variabile casuale
T=
X n − µ0
Sn
n
che segue la distribuzione t di Student. Il campione ha n = 25 pertanto la t di Student è con 24
gradi di libertà.
Data la forma della ipotesi H0 il test è di tipo "unilaterale" e dalle tabelle si ricava il valore critico
della T per la H0 che risulta tc0 = + 2,492
La regione di rifiuto della H0 è pertanto T > tc0 = + 2,492
µ 0 − µ1
è possibile ricavare il valore critico della t di Student
Sn n
relativo alla ipotesi H1 che risulta tc1 = - 2,508:
ricordando che
tc1 = tc 0 +
Dal valore della tc1 = - 2,508:si individua il corrispondente valore di β che risulta compreso fra
0,005 e 0,01. Da questi valori si ricava la potenza del test (potenza = 1 – β ): il test può essere
condotto in quanto la potenza che esprime contro H1 è superiore al minimo richiesto nella specifica
del test.
Risultato del test
Il valore tn della variabile T calcolata a partire dai valori corrispondenti al campione esaminato è:
T=
X n − µ0
48 − 45
⇒ tn =
= +3
Sn
5
25
n
Il valore tn della T cade nella regione di rifiuto della H0 e, con una fiducia del 99%, si può
sostenere che le RAM acquistate hanno un assorbimento tipico maggiore di quello dei dispositivi
prodotti con il nuovo processo.
Pinco Pallo rifiuterà la fornitura delle memorie che gli stavano per essere vendute come
prodotte mediante il nuovo processo.