Principi di genetica - Robert J. Brooker
Copyright © 2010 – The McGraw-Hill Companies srl
SOLUZIONI AI PROBLEMI DEL CAPITOLO 5
Domande concettuali
C1. Ricombinazione genetica è un termine che si riferisce alla presenza di una nuova combinazione di alleli in un
individuo della progenie. Il crossing-over è un evento fisico che coinvolge lo scambio di segmenti di materiale
genetico tra due cromosomi.
C2. L’ipotesi di assortimento indipendente viene usata perché ci permette di calcolare i valori attesi sulla base dei
rapporti mendeliani. Utilizzando i valori osservati e attesi, possiamo calcolare se le deviazioni tra questi due valori
siano, o meno, troppo grandi per essere dovute al caso. Se le deviazioni sono elevate, rifiutiamo l’ipotesi di
assortimento indipendente.
C3. La ricombinazione mitotica è il crossing-over tra cromosomi omologhi durante la mitosi nelle cellule somatiche.
La ricombinazione mitotica può spiegare un macchia blu. In seguito alla ricombinazione mitotica, i due
cromosomi che portano l'allele b possono segregare nella stessa cellula e produrre il colore blu. Un'altra ragione
potrebbe essere la perdita del cromosoma; il cromosoma che porta l'allele B potrebbe venire perso durante la
mitosi.
C4. Se i cromosomi (sulla destra) indicati con 2 e 4 si muovono verso la cellula figlia, si otterrà una macchia di colore
albino e mantello a pelo lungo. L’altra cellula riceverà i cromosomi 1 e 3, e produrrà una macchia nera con
mantello a pelo corto.
C5. A. 1 e 4
B.
2e3
C.
2 e 4, oppure 1 e 3
C6. Un singolo crossing-over produce A B C, A b c, a B C, e a b c.
A. Tra 2 e 3, tra i geni B e C
B. Tra 1 e 4, tra i geni A e B
C. Tra 1 e 4, tra i geni B e C
D. Tra 2 e 3, tra i geni A e B
C7. Ci sono 7 cromosomi per genoma aploide. Se dividiamo 20 000 per 7, ci sono, in media, circa 2857 per
cromosoma.
C8. La probabilità di centrare il canestro sarebbe maggiore se il canestro fosse più grande. In modo simile, la
probabilità che un crossing-over abbia inizio in una regione compresa tra due geni è proporzionale alla
dimensione della regione tra i due geni. C’è un numero finito (solitamente piccolo) di crossing-over che si
verificano tra cromosomi omologhi durante la meiosi, e la probabilità che si verifichi un crossing-over in una
regione tra due geni dipende dalla dimensione di questa regione.
Principi di genetica - Robert J. Brooker
Copyright © 2010 – The McGraw-Hill Companies srl
C9. Se il pisello dolce ha sette gruppi di associazione, questo significa che esso possiede sette cromosomi per
complemento aploide. Il pisello dolce è diploide, quindi possiede due assetti cromosomici. Perciò, nelle cellule
delle foglie del pisello dolce si trovano 14 cromosomi.
C10. Il pedigree suggerisce un’associazione tra l’allele dominante che causa la sindrome unghia-rotula e l’allele IB del
gene dei gruppi sanguigni AB0. In ogni caso, l’individuo che eredita IB eredita anche questa malattia.
C11. Le quattro categorie fenotipiche per la generazione F2 sono: mantello marrone, coda corta; mantello marrone, coda
lunga; mantello bianco, coda corta, e mantello bianco, coda lunga. I ricombinanti sono: mantello marrone, coda
lunga, e mantello bianco, coda corta. Gli individui della generazione F2 saranno presenti in rapporto 1:1:1:1 se i
due geni non sono associati. In altre parole, le quattro categorie fenotipiche rappresenteranno ciascuna il 25%. Se i
geni sono associati, la progenie ricombinante sarà presente in percentuale minore.
C12. Ass-1
43
Sdh-1
5
Hdc
9
Hao-1 6
Odc-2
8
Ada-1
C13. Utilizziamo la regola del prodotto. La probabilità di un doppio crossing-over è 0,1 x 0,1, che equivale a 0,01, ossia
all'1%. La probabilità di un triplo crossing-over è 0,1 x 0,1 x 0,1 = 0,001, ovvero 0,1%. L'interferenza positiva
renderebbe questi valori inferiori.
C14. L’impossibilità di identificare i doppi crossing-over comporta che la distanza di mappa venga sottostimata. In altri
termini, in quella regione si verificano più crossing-over di quanti ne possiamo visualizzare. Quando avviene un
doppio crossing-over, non abbiamo progenie ricombinante (in un incrocio diibrido). Perciò, il secondo crossingover cancella gli effetti del primo evento di scambio.
C15. La distanza di mappa tra i geni A e B risulterebbe maggiore rispetto a quella tra C e D a causa della maggiore
frequenza del crossing-over. Otterremmo un numero maggiore di progenie ricombinante rispetto ai geni A e B,
quindi la distanza di mappa calcolata sarebbe superiore, anche se la distanza fisica tra A e B, e tra C e D, è
identica.
C16. La caratteristica chiave è che tutti i prodotti di una singola meiosi sono contenuti in un unico sacco. Le spore di
questo sacco possono essere dissezionate, e i loro caratteri genetici possono essere analizzati singolarmente.
C17. Una tetrade contiene quattro spore; un'ottade ne contiene otto. In una tetrade la meiosi produce quattro spore. In
un'ottade la meiosi è seguita da una divisione mitotica che raddoppia il numero di cellule a otto.
C18. In un asco non ordinato, i prodotti di una meiosi sono liberi di muoversi. In un’ottade ordinata (o tetrade), essi
sono allineati secondo le loro relazioni durante la meiosi e la mitosi. Un’ottade ordinata può essere utile per
mappare la distanza tra un singolo gene e il centromero.
C19. Potrebbe essere una disposizione 2:2:2:2 oppure 2:4:2.
C20. La percentuale sarebbe maggiore per il gene A. La tipica distribuzione dei segreganti in prima divisione si verifica
quando non avviene un crossing-over tra il centromero e il gene di interesse. Siccome il gene A è più vicino al
centromero che al gene B, è meno probabile avere uno scambio genetico tra il gene A e il centromero. Questo
renderebbe più probabile osservare dei segreganti in prima divisione.
Domande sperimentali (Includono in maggioranza domande sulla mappatura)
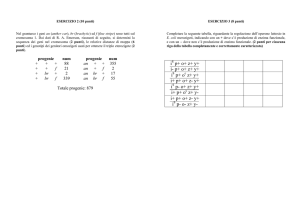
S1. Se ipotizziamo che i due geni assortiscano in modo indipendente, il rapporto previsto è 9:3:3:1. Il numero totale di
individui della progenie è 427. I numeri attesi sono
9/16 × 427 = 240 fiori porpora, polline allungato
3/16 × 427 = 80 fiori porpora, polline rotondo
3/16 × 427 = 80 fiori rossi, polline allungato
1/16 × 427 = 27 fiori rossi, polline rotondo
Inserendo questi valori nella formula del chi quadrato, assieme ai numeri osservati, otteniamo
χ2 = (296 – 240)2 / 240 + (19 – 80)2 / 80 + (27 – 80)2 / 80 + (85 – 27)2 / 27
χ2 = 13,1 + 46,5 + 35,1 + 124,6
χ2 = 219,3
Cercando questo valore nella tabella del chi quadrato in corrispondenza di 3 gradi di libertà, riscontriamo che
questo grande valore sarebbe effetto del caso in meno dell'1% degli eventi. Perciò, rifiutiamo l'ipotesi che i geni
assortiscano in modo indipendente e concludiamo che i geni sono associati.
Principi di genetica - Robert J. Brooker
Copyright © 2010 – The McGraw-Hill Companies srl
S2. Essi avrebbero potuto utilizzare un ceppo con due cromosomi aberranti. In questo caso, i cromosomi ricombinanti
apparirebbero normali oppure con anomalie a entrambe le estremità.
S3. La parte superiore della colonna “Conceptual level” nella Figura EG5.1.1 (Esperimento di genetica 5.1 sul sito
internet) illustra i cromosomi dell'incrocio della McClintock. Per renderlo un reincrocio standard questo
esperimento potrebbe essere modificato nel seguente modo. Nel parentale eterozigote, gli alleli C (colorato) e Wx
(amidaceo) potrebbero trovarsi nel cromosoma che presenta l'elemento knob, e gli alleli c (incolore) e wx (ceroso)
sul cromosoma normale. L'altro parentale avrebbe due copie normali (dal punto di vista citologico) del
cromosoma 9 e sarebbe omozigote per gli alleli recessivi ( cioè cc wxwx). Se venisse eseguito questo incrocio, la
progenie non ricombinante sarebbe colorata e amidacea, oppure incolore e cerosa; la progenie ricombinante
sarebbe colorata e cerosa, oppure incolore e amidacea. La progenie ricombinante dovrebbe ereditare un
cromosoma con un elemento knob ma non presenterebbe la traslocazione, oppure avrebbe la traslocazione ma
senza knob.
S4. Nei mammiferi un gene che si trova sul cromosoma Y viene trasmesso solo da maschio a maschio. Sarebbe
difficile mappare geneticamente i geni associati al cromosoma Y perché un maschio normale ha solo una copia del
cromosoma Y, per cui non è possibile che si verifichi alcun crossing-over tra due cromosomi Y. Occasionalmente
nascono dei maschi anomali (XYY) con due cromosomi Y. Se questi maschi fossero eterozigoti per gli alleli dei
geni Y-linked, si potrebbe analizzare la progenie maschile normale dei parentali XYY e verificare se sia avvenuto
un crossing-over.
S5. La logica alla base del reincrocio è quella di determinare se nel parentale eterozigote si è verificata
ricombinazione durante la meiosi. L'altro parentale è solitamente un omozigote recessivo, quindi non è possibile
determinare se è avvenuto crossing-over in questo parentale. È più semplice interpretare i dati se un reincrocio
impiega un parentale omozigote recessivo. Tuttavia, non è necessario che nell'altro parentale tutti gli alleli
dominanti siano su un cromosoma e tutti gli alleli recessivi sull'altro cromosoma. La generazione parentale ci
fornisce le informazioni riguardanti il tipo di associazione originale tra gli alleli dominanti e quelli recessivi.
S6. La risposta è fornita nel problema risolto R5. Non è possibile ottenere una frequenza di ricombinanti maggiore del
50% perché la distribuzione dei crossing-over multipli può produrre solo un valore medio massimo del 50%. Se
un reincrocio produce un valore del 50% di progenie ricombinante, questo può avere due significati diversi. I due
geni sono su due cromosomi distinti, oppure i due geni sono sullo stesso cromosoma ma distanti tra loro almeno
50 u.m..
S7. La ragione per cui la percentuale della progenie ricombinante è più accurata quando i geni sono strettamente
associati è che si verifica un numero minore di doppi crossing-over. L'impossibilità di identificare i doppi
crossing-over è alla base della sottostima della distanza di mappa. Se due geni sono strettamente associati, si
verificano rari doppi crossing-over, quindi la sottostima è minima.
S8. Se due geni si trovano a una distanza di almeno 50 u.m., dovresti mappare degli altri geni tra loro per dimostrare
che essi sono effettivamente sullo stesso gruppo di associazione. Per esempio, se il gene A si trovasse a 55 u.m.
dal gene B, ci potrebbe essere un terzo gene (per esempio C) localizzato a 20 u.m da A e 35 u.m. da B. Questi
risultati indicherebbero che A e B si trovano a 55 u.m. di distanza, assumendo che i reincroci a due punti tra i geni
A e B producano il 50% di progenie ricombinante.
S9. Morgan lo determinò analizzando i geni a coppie. Questa analisi rivelò che c'era un numero inferiore di
ricombinanti tra certe coppie di geni (per esempio il colore del corpo e il colore degli occhi) rispetto ad altre
coppie di geni (il colore degli occhi e la lunghezza delle ali). Da questo confronto, egli ipotizzò che i geni
strettamente associati sullo stesso cromosoma produrranno meno ricombinanti rispetto ai geni lontani.
S10. Sturtevant utilizzò i dati che riguardavano le seguenti coppie: y e w, w e v, v e r, e v e m.
S11. Distanza di mappa:
(64 + 58) / (333 + 64 + 58 + 380) x 100 = 15,1 u.m.
S12. A. Siccome essi sono a 12 u.m. di distanza, ci aspettiamo il 12% (ossia 120) di progenie ricombinante. Questo
corrisponde approssimativamente a 60 Aabb e 60 aaBb più 440 AaBb e 440 aabb.
B. Ci aspetteremmo 60 AaBb, 60 aabb, 440 Aabb, e 440 aaBb.
S13. Consideriamo i geni a coppie: il 10% della progenie dovrebbe essere il risultato del crossing-over tra i geni A e B,
e il 5% dovrebbe essere il frutto del crossing-over tra A e C.
A. Questo genotipo è conseguenza di un crossing-over tra B e A. I parentali sono Aa bb Cc e aa Bb cc. Il 10%
dei ricombinanti sono Aa Bb Cc e aa bb cc. Se assumiamo che vi sia un uguale numero dei due tipi di
ricombinanti, il 5% sono Aa Bb Cc.
Principi di genetica - Robert J. Brooker
Copyright © 2010 – The McGraw-Hill Companies srl
B. Questo genotipo è conseguenza di un crossing-over tra A e C. I parentali sono Aa bb Cc e aa Bb cc. Il 5% dei
ricombinanti sono aa Bb Cc e Aa bb cc. Se assumiamo che vi sia un uguale numero dei due tipi di ricombinanti,
2,5% di essi sono aa Bb Cc.
C. Anche questo genotipo è conseguenza di un crossing-over tra A e C. I parentali sono Aa bb Cc e aa Bb cc. Il
5% dei ricombinanti sono aa Bb Cc e Aa bb cc. Se assumiamo che vi sia un uguale numero dei due tipi di
ricombinanti, il 2,5% di essi è Aa bb cc.
S14. A causa della grande distanza tra i due geni, essi assortiranno in modo indipendente anche se si trovano in realtà
sullo stesso cromosoma. Secondo l’assortimento indipendente, ci aspettiamo 50% di progenie di tipo parentale e
50% ricombinante. Perciò, questo incrocio produrrà 150 individui per ciascuna delle quattro categorie.
S15. A. La strategia fondamentale per risolvere questo problema è quella di dividere i dati in coppie di geni e
determinare la distanza di mappa tra due geni.
184 alte, buccia liscia
13 alte, buccia vellutata
184 nane, buccia vellutata
12 nane, buccia liscia
Distanza di mappa = (13 + 12) / (184 + 13 + 184 + 12) = 6,4 u.m.
153 alte, forma normale
44 alte, forma ovale
155 nane, forma ovale
41 nane, forma normale
Distanza di mappa = (44 + 41) / (153 + 44 + 155 + 41) = 21,6 u.m.
163 buccia liscia, forma normale
33 buccia liscia, forma ovale
31 buccia vellutata, forma normale
166 buccia vellutata, forma ovale
Distanza di mappa = (33 + 31) / (163 + 33 + 31 + 166) = 16,3 u.m.
Utilizzando le due distanze più corte per calcolare la distanza di mappa:
Alte/ nane
6,4
Buccia liscia/vellutata
16,3
Forma normale/ovale
S16. A. Se ipotizziamo che i due geni assortiscano in modo indipendente, il rapporto previsto è 1:1:1:1, di cui 50%
parentali e 50% ricombinanti. La progenie è costituita da un totale di 390 individui, di cui 232 con fenotipo
parentale e 158 con fenotipo ricombinante. Il numero atteso di progenie ricombinante è 195, lo stesso valore è
atteso per le classi parentali. Inserendo questi dati nella formula per il calcolo del chi quadrato,
χ2 = (232 – 195)2 / 195 + (158 – 195)2 / 195
χ2 = 7.02 + 7.02
χ2 = 14,04
Confrontando questo valore con quello che nella tabella del chi quadrato compare alla riga corrispondente ad un
grado di libertà, dobbiamo rifiutare l’ipotesi, perché il valore di chi quadrato è superiore a 3,841.
B. Distanza di mappa:
Distanza di mappa = (78 + 80) / (117 + 115 + 78 + 80)
= 40,5 u.m.
Siccome il valore si avvicina a 50 u.m., questa è probabilmente una sottostima della reale distanza tra questi
due geni.
S17. Nel reincrocio, i due parentali saranno omozigoti che non possono produrre alcun enzima, mentre gli eterozigoti
possono sintetizzare entrambi gli enzimi. I ricombinanti produrranno un enzima, ma non entrambi. Siccome i due
geni distano 12 u.m., il 12% della progenie sarà ricombinante e l'88% sarà di tipo parentale. Dato che i due tipi
Principi di genetica - Robert J. Brooker
Copyright © 2010 – The McGraw-Hill Companies srl
parentali sono prodotti in numero uguale, ci aspettiamo che il 44% dei topi sia incapace di produrre uno dei due
enzimi.
S18. La percentuale di ricombinanti per colore e forma del baccello (verde, giallo e largo, oppure stretto) è 7%, ovvero
0,07; ci dovrebbe essere il 3,5% di verde, stretto e 3,5% di giallo, largo. Il rimanente 93% dei tipi parentali
dovrebbe essere per il 46,5% verde, largo e per il 46,5% sarà giallo, stretto. Il terzo gene assortisce in modo
indipendente. Ci aspettiamo il 50% di baccelli lunghi e il 50% di baccelli corti nei confronti di ciascuno degli altri
due geni. Per calcolare i numeri di progenie su un totale di 800 individui, moltiplichiamo 800 per la percentuale di
ciascuna categoria.
(0,465 verde, largo) (0,5 lungo) (800) = 186 verde, largo, lungo
(0,465 giallo, stretto) (0,5 lungo) (800) = 186 giallo, stretto, lungo
(0,465 verde, largo) (0,5 corto) (800) = 186 verde, largo, corto
(0,465 giallo, stretto) (0,5 corto) (800) = 186 giallo, stretto, corto
(0,035 verde, stretto) (0,5 lungo) (800) = 14 verde, stretto, lungo
(0,035 giallo, largo) (0,5 lungo) (800) = 14 giallo, largo, lungo
(0,035 verde, stretto) (0,5 corto) (800) = 14 verde, stretto, corto
(0,035 giallo, largo) (0,5 corto) (800) = 14 giallo, largo, corto
S19. A. Se indichiamo con B (coda folta) e b (coda normale) gli alleli di un gene, e Y (giallo) e y (bianco) quelli del
secondo gene:
Generazione parentale: BBYY × bbyy
Generazione F1: Tutti BbYy (NOTA: se i due geni fossero associati, B sarebbe associato a Y e b a y).
Reincrocio: F1 BbYy x bbyy
Progenie non ricombinante del reincrocio: BbYy e bbyy
Maschi BbYy —coda folta, gialli
Maschi bbyy — coda normale, bianchi
Femmine BbYy —coda normale, gialli
Femmine bbyy —coda normale, bianchi
Progenie ricombinante del reincrocio: Bbyy e bbYy
Maschi Bbyy —coda folta, bianchi
Maschi bbYy —coda normale, gialli
Femmine Bbyy —coda normale, bianchi
Femmine bbYy —coda normale, gialli
Non possiamo utilizzare i dati relativi alla progenie femminile perché non possiamo sapere se le femmine sono
ricombinanti oppure non ricombinanti in quanto tutte le femmine hanno coda normale. Tuttavia, possiamo capire
se i maschi sono ricombinanti.
Se utilizziamo i dati relativi ai maschi per eseguire un'analisi del chi quadrato, ci aspettiamo un rapporto 1:1:1:1
nella progenie maschile. Il numero totale dei maschi nella progenie è 197, quindi ci aspettiamo ¼, ossia 49
(arrotondato a numero intero) dei quattro possibili fenotipi. Per calcolare il chi quadrato:
χ2 = (28 – 49)2 / 49 + (72 – 49)2 / 49 + (68 – 49)2 / 49 + (29 – 49)2 / 49
χ2 = 9,0 + 10,8 + 7,4 + 8,2
χ2 = 35,4
Verificando questo valore nella tabella del chi quadrato in corrispondenza di 3 gradi di libertà, troveremo che il
valore supera di molto il livello di probabilità di 0,01. Quindi, è molto improbabile ottenere una così grande
deviazione se la nostra ipotesi di assortimento indipendente fosse corretta. Di conseguenza, rifiutiamo la nostra
ipotesi e concludiamo che i geni sono associati.
B. Per calcolare la distanza di mappa:
(28 + 29) / (28 + 72 + 68 + 29) = 28,9 u.m.
S20. Usiamo i seguenti simboli: G per baccelli verdi, g per i baccelli gialli, S per le plantule verdi, s per le plantule
verde-blu, C per le piante normali, c per le piante cascanti. L’incrocio parentale è GG SS CC per gg ss cc. Le
piante della generazione F1 saranno tutte Gg Ss Cc. Se i geni fossero associati, gli alleli G, S, e C si troverebbero
su uno stesso cromosoma, mentre gli alleli g, s, c sarebbero associati sul cromosoma omologo.
Principi di genetica - Robert J. Brooker
Copyright © 2010 – The McGraw-Hill Companies srl
Il reincrocio coinvolge le piante F1, quindi Gg Ss Cc con gg ss cc.
Per misurare le distanze tra i geni, possiamo suddividere i dati in coppie di geni.
Colore del baccello, colore della plantula
2210 baccelli verdi, plantule verdi – non ricombinante
296 baccelli verdi, plantule verde-blu – ricombinante
2198 baccelli gialli, plantule verde-blu – non ricombinante
293 baccelli gialli, plantule verdi – ricombinante
Distanza di mappa = (296 + 293) / (2210 + 296 + 2198 + 293) x 100 = 11,8 u.m.
Colore del baccello, altezza della pianta
2340 baccelli verdi, piante normali – non ricombinante
166 baccelli verdi, pianta cascante – ricombinante
2323 baccelli gialli, pianta cascante – non ricombinante
168 baccelli gialli, piante normali – ricombinante
Distanza di mappa = (166 + 168) / (2340 + 166 + 2323 + 168) x 100 = 6,7 u.m.
Colore della plantula, altezza della pianta
2070 plantule verdi, piante normali – non ricombinante
433 plantule verdi, pianta cascante – ricombinante
2056 plantule verde-blua, pianta cascante – non ricombinante
438 plantule verde-blu, piante normali – ricombinante
Distanza di mappa = (433 + 438) / (2070 + 433 + 2056 + 438) x 100 = 17,4 u.m.
L’ordine dei geni è: colore delle plantule, colore dei baccelli, e altezza della pianta (oppurel’ordine opposto). Il
gene per il colore del baccello è posto nel mezzo. Se utilizziamo le due distanze più brevi per costruire la nostra
mappa:
S
11,8 G
6,7
C
S21. Utilizziamo i seguenti simboli: S per il naso normale, s per il naso schiacciato, p per la coda normale, P per la
coda a punta, J per l'andatura normale, j per l'andatura a scatto.
L'incrocio parentale è ss PP jj per SS pp JJ.
La progenie F1 sarà tutta Ss Pp Jj. Se i geni fossero associati, gli alleli s, P, e j sarebbero sullo stesso cromosoma,
e gli alleli S, p, e J sarebbero associati sul cromosoma omologo.
Il reincrocio avviene tra i topi F1, che sono Ss Pp Jj, e i topi ss pp jj.
Per misurare le distanze tra i geni, possiamo dividere i dati in coppie.
Forma del naso, lunghezza della coda
631 naso schiacciato, coda a punta—non ricombinante
111 naso schiacciato, coda normale— ricombinante
625 naso normale, coda normale—non ricombinante
115 naso normale, coda a punta—ricombinante
Distanza di mappa = (111 + 115) / (631 + 111 + 625 + 115) x 100 = 15,2 u.m.
Forma del naso, andatura
662 naso schiacciato, andatura a scatto—non ricombinante
80 naso schiacciato, andatura normale— ricombinante
652 naso normale, andatura normale—non ricombinante
115 naso normale, andatura a scatto—ricombinante
Principi di genetica - Robert J. Brooker
Copyright © 2010 – The McGraw-Hill Companies srl
Distanza di mappa = (80 + 88) / (662 + 80 + 652 + 88) x 100 = 11,3 u.m.
Lunghezza della coda, andatura
571 coda a punta, andatura a scatto—non ricombinante
175 coda a punta, andatura normale— ricombinante
557 coda normale, andatura normale—non ricombinante
179 coda normale, andatura a scatto—ricombinante
Distanza di mappa = (175 + 179) / (571 + 175 + 557 + 179) x 100 = 23,9 u.m.
L'ordine dei geni è lunghezza della coda, forma del naso, e andatura normale (oppure l'ordine opposto). La forma
del naso è nel mezzo.
Se utilizziamo le distanze più brevi per costruire la nostra mappa:
P
15,2
S
11,3
J
S22. Per rispondere a questa domanda possiamo considerare i geni a coppie. Consideriamo le coppie di geni che sono
più vicini tra loro. La distanza tra i geni per la lunghezza delle ali e il colore degli occhi è 12,5 u.m.. Da questo
incrocio, ci aspettiamo che l’87,5% della progenie abbia ali lunghe e occhi rossi oppure ali corte e occhi porpora,
e il 12,5 % abbia ali lunghe e occhi porpora, oppure ali corte e occhi rossi. Perciò ci aspettiamo che il 43,75%
abbia ali lunghe e occhi rossi, e il 43,75% ali corte e occhi porpora, mentre il 6,25% abbia ali lunghe e occhi
porpora, e il 6,25% ali corte e occhi rossi. Se abbiamo 1000 moscerini, prevediamo che 438 abbiano ali lunghe e
occhi rossi, 438 ali corte e occhi porpora, 62 ali lunghe e occhi porpora, e 62 ali corte e occhi rossi (arrotondando
a valore intero)
La distanza tra i geni per il colore degli occhi e il colore del corpo è 6 u.m. Da questo incrocio, ci attendiamo il
94% con combinazioni di tipo parentale (occhi rossi e corpo grigio, oppure occhi porpora e corpo nero) e il 6%
con una combinazione di alleli non parentale (occhi rossi e corpo nero oppure occhi porpora e corpo grigio).
Quindi, dei 438 moscerini con ali lunghe e occhi rossi, il 94% di loro (che equivale a circa 412) dovrebbe avere ali
lunghe, occhi rossi, e corpo grigio, e il 6% di essi (ossia circa 26) ali lunghe, occhi rossi, e corpo nero. Dei 438
moscerini con ali corte e occhi porpora, ci aspettiamo che circa 412 abbiano ali corte, occhi porpora, e corpo nero,
mentre 26 abbiano ali corte, occhi porpora, e corpo grigio.
Dei 62 moscerini con ali lunghe e occhi porpora, il 94% di essi (ossia circa 58) dovrebbe avere ali lunghe, occhi
porpora e corpo nero, e il 6% (ovvero circa 4) ali lunghe, occhi porpora, e corpo grigio. Dei 62 moscerini con ali
corte e occhi rossi, ci aspettiamo che il 94% (ossia circa 58) abbia ali corte, occhi rossi, e corpo grigio, e il 6%
(ossia circa 4) abbia ali corte, occhi rossi, e corpo nero.
Riassumendo,
Ali lunghe, occhi rossi, corpo grigio
412
Ali lunghe, occhi porpora, corpo grigio
4
Ali lunghe, occhi rossi, corpo nero
26
Ali lunghe, occhi porpora, corpo nero
58
Ali corte, occhi rossi, corpo grigio
58
Ali corte, occhi porpora, corpo grigio
26
Ali corte, occhi rossi, corpo nero
4
Ali corte, occhi porpora, corpo nero
412
I moscerini con ali lunghe, occhi porpora, e corpo grigio, oppure con ali corte, occhi rossi, e corpo nero, vengono
prodotti da un evento di doppio crossing-over.
S23. A.
Parentale
Parentale
Principi di genetica - Robert J. Brooker
Copyright © 2010 – The McGraw-Hill Companies srl
Progenie
B. Un individuo eterozigote della generazione F2 erediterà un cromosoma che porta tutti gli alleli dominanti. Nel
parentale F1 un crossing-over nella regione di 7 u.m. tra i geni b e A (e tra B e a) produrrebbe un cromosoma B A
C e b a c. Se un individuo della generazione F2 ereditasse il cromosoma BAC dal suo parentale F1 e il cromosoma
bac dal parentale omozigote, esso sarebbe eterozigote per i tre geni.
C. Dalla risposta B abbiamo imparato che un crossing-over tra i geni b e A (e tra B e a) produrrebbe i
cromosomi BAC e bac. Se un individuo ereditasse il cromosoma bac dal suo parentale F1 e il cromosoma bac dal
parentale omozigote, esso sarebbe omozigote per i tre geni. La probabilità di crossing-over in questa regione è del
7%. Tuttavia, la metà degli eventi produce cromosomi BAC e l'altra metà produce cromosomi bac. Perciò, le
probabilità di avere progenie F2 omozigote è 3,5% .
S24. Sì. Iniziamo con le femmine, che sono XNl XnL. Queste femmine devono essere incrociate con maschi XNLY
perché un maschio vivo non può essere portatore dell’allele n oppure l. In assenza di crossing-over, un
accoppiamento tra femmine XNlXnL con maschi XNLY non dovrebbe produrre progenie maschile viva. Tuttavia,
durante l’oogenesi in questi topi femmina eterozigoti, potrebbe verificarsi un evento di scambio nella regione
compresa tra i due geni, che produrrebbe un cromosoma XNL e un cromosoma Xnl. La progenie maschile che
eredita questi cromosomi ricombinanti sarà XNLY oppure XnlY (mentre i maschi non ricombinanti saranno XnLY
oppure XNlY). Solo i topi maschi che ereditano la combinazione XNLY saranno vitali. I maschi vivi rappresentano
solo la metà della progenie ricombinante (l’altra metà è XnlY, e nascono morti.)
Per calcolare la distanza di mappa:
Distanza di mappa = 2 (Numero di invididui maschi vivi nella progenie) / (Numero di maschi nati morti +
Numero di maschi nati vivi) x 100
S25. A. La prima cosa da fare è determinare quali aschi sono ditipi parentali (DP), ditipi non parentali (DNP) e
tetratipi (T). Un ditipo parentale conterrà una disposizione 2:2 delle spore con gli stessi genotipi dei parentali
aploidi originali. La combinazione di 502 aschi sono ditipi parentali. I ditipi non parentali sono quelli contenenti
una disposizione 2:2 di genotipi diversi da quelli parentali. La combinazione di 4 aschi si adatta a questa
descrizione. Infine, i tetratipi contengono una disposizione 1:1:1:1 dei genotipi, metà dei quali hanno un genotipo
parentale e metà hanno un genotipo non parentale. Ci sono 312 tetratipi in questo caso. Calcolando la distanza di
mappa:
Distanza di mappa = [DNP + (1/2) (T) / Numero totale di aschi] x 100
= 4 + (½)(312) / 818
= 19,6 u.m.
Se utilizziamo l'equazione più accurata per calcolare la distanza di mappa:
Distanza di mappa = [T + 6DNP / Numero totale di aschi] x 0,5 x 100
= 312 + (6)(4) / 818
= 20,5 u.m.
B. La frequenza dei singoli crossing-over è 0,205 se utilizziamo l'equazione più accurata
C. I ditipi non parentali sono prodotti dai doppi crossing-over. Per calcolare il numero atteso, moltiplichiamo
0,205 x 0,205 = 0,042, ossia 4,2%. In un totale di 818 aschi, ci aspettiamo che 34,3 aschi siano il prodotto di un
doppio crossing-over. Tuttavia, come illustrato nella Figura 5.13, solamente 1/4 di essi apparterranno alla
categoria ditipo non parentale. Perciò, moltiplichiamo 34,3 per 1/4, e otteniamo un valore di 8,6 ditipi non
parentali determinati da un doppio crossing-over. Dato che ne abbiamo osservati solamente 4, questo calcolo ci
suggerisce che vi è interferenza positiva.
S26. Distanza di mappa = (1/2) (M2) / Totale x 100
= (1/2) (22 + 21 + 21 + 23) / (22 + 21 + 21 + 21 + 451 + 23 + 455) x 100
= 4,4 u.m.
Principi di genetica - Robert J. Brooker
Copyright © 2010 – The McGraw-Hill Companies srl
S27. A. Tipi
B. Numero