Lez. 14 - Momento angolare

Lez. 15 – Momento angolare
Prof. Giovanni Mettivier
1
Dott. Giovanni Mettivier, PhD
Dipartimento Scienze Fisiche
Università di Napoli “Federico II”
Compl. Univ. Monte S.Angelo
Via Cintia, I-80126, Napoli
[email protected]
+39-081-676137
2
Assimiliamo un corpo rigido ad un insieme di
particelle e assumiamo che esso ruoti attorno a un
asse fisso z con una velocità angolare ω. Ciascuna
particella del corpo è in moto cosicché ha una certa
energia cinetica determinata dalla massa e dalla
velocità tangenziale. Se mi è la massa dell’i-esima
particella, e la sua velocità tangenziale è vi, l’energia
cinetica di questa particella è
Ki =
1
mi vi2
2
_________________________________________________________________________________________________
3
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Possiamo esprimere l’energia cinetica totale KR del
corpo rigido in rotazione come la somma delle energie
cinetiche delle singole particelle. Quindi
1
1
1

K R = ∑ K i = ∑ mi vi2 = ∑ mi ri 2ω 2 =  ∑ mi ri 2 ω 2
2 i
2 i
i
i 2

dove nella somma abbiamo messo in evidenza ω2
poiché è uguale per tutte le particelle del corpo. La
grandezza in parentesi è chiamata il momento
d’inerzia I del corpo rigido: I = m r 2
∑
i i
i
Quindi, possiamo esprimere l’energia cinetica del
corpo rigido che ruota attorno alla asse z come
KR =
1 2
Iω
2
_________________________________________________________________________________________________
4
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Il momento di inerzia è una misura dell’opposizione del
sistema alla variazione della sua velocità angolare.
Esso gioca nel moto rotazionale un ruolo analogo a
quello della massa in tutte le equazioni relative ai moti
translazionali. Da notare che il momento di inerzia
dipende non solo dalla massa del corpo rigido ma
anche da come la massa è distribuita attorno all’asse
di rotazione.
_________________________________________________________________________________________________
5
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Per un corpo esteso e continuo
I = lim
∆mi → 0
∑ r ∆m = ∫ r dm
2
i
2
i
i
I = ∫ ρr 2 dV
_________________________________________________________________________________________________
6
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
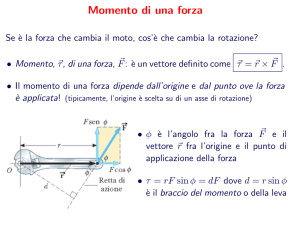
Quando su un corpo rigido imperniato su un certo asse si
esercita una forza risultante e la retta d’azione della forza
non passa attraverso il perno, il corpo tende a ruotare
attorno a quest’asse. La tendenza di una forza a far
ruotare un corpo attorno a un certo asse si misura con
una grandezza vettoriale chiamata momento della
forza.
forza
La forza applicata F generalmente
agisce formando un angolo φ
rispetto al vettore posizione r che
localizza il punto di applicazione
della forza. Definiamo il momento
della forza τ dovuto alla forza F
con l’espressione
τ ≡ rFsenφ
_________________________________________________________________________________________________
7
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
E’ estremamente importante convincersi che il
momento della forza è definito quando è specificato
un particolare asse di riferimento, rispetto al quale è
definita la distanza r.
La componente Fcosφ parallela a r non causerà una
rotazione attorno all’asse del perno, poiché la sua retta
d’azione passa proprio per il perno. Soltanto la
componente perpendicolare Fsenφ causa una rotazione
attorno all’asse del perno.
_________________________________________________________________________________________________
8
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Se si associa la funzione seno alla distanza r,
τ = rFsenφ = F(rsenφ) = Fd
La grandezza d = rsenφ, chiamata braccio del
momento (o braccio della leva),
leva o semplicemente
braccio della forza F, rappresenta la distanza fra l’asse
di rotazione e la retta d’azione di F.
_________________________________________________________________________________________________
9
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Se vi sono due o più forze che agiscono sul corpo
rigido ciascuna di esse tende a produrre una rotazione
intorno all’asse per O. Useremo la convenzione che il
segno del momento della forza è positivo quando la
forza tende a produrre una rotazione antioraria, mentre
è negativo quando la rotazione favorita è quella oraria.
Il momento risultante che agisce sul corpo rigido
rispetto all’asse passante per O è, quindi
τris = τ1 + τ2 = F1d1 – F2d2
_________________________________________________________________________________________________
10
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Il vettore momento della forza può essere definito come
il prodotto vettoriale di r ed F
r r
τ ≡ r xF
r
_________________________________________________________________________________________________
11
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Abbiamo, adesso, due condizioni
necessarie per l’equilibrio di un
corpo, che possono essere fissate
come segue:
- La risultante delle forze esterne
deve essere uguale a zero:
r
F
∑ =0
- la risultante dei momenti delle forze
esterne deve essere uguale a zero
rispetto a qualsiasi asse:
r
∑τ = 0
_________________________________________________________________________________________________
12
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Una scala uniforme di lunghezza l e massa m è
appoggiata contro una parete verticale liscia. Se il
coefficiente di attrito statico fra la scala e il suolo è µs =
0.4, trovare l’angolo minimo θmin per il quale la scala
non scivola,
∑F = f −P = 0
∑ F = n − mg = 0
x
s
y
∑τ
0
l
= Plsenθ − mg cos θ = 0
2
tan θ min =
mg
n
n
1
=
=
=
= 1.25
2 P 2 f s ,max 2( µ s n) 2(0.4)
θ min = 51°
_________________________________________________________________________________________________
13
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Ogni forza applicata può essere rappresentata per
mezzo delle sue componenti radiale e tangenziale. La
componente radiale di una forza applicata non
contribuisce al momento risultante poiché la sua retta
d’azione passa per l’asse di rotazione. Quindi, solo la
componente tangenziale di una forza applicata
contribuisce al momento.
Per ogni data particella, descritta dall’indice di variabile
i, entro il corpo rigido, possiamo
Fti=miati
dove il pedice t si riferisce alla componenti tangenziali.
Moltiplichiamo ambedue i membri di questa
espressione per ri, la distanza della particella dell’asse
di rotazione:
riFti = rimiati
_________________________________________________________________________________________________
14
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Usando l’eq e ricordando la definizione di momento
meccanico (τ=rFsenφ=rFt ), possiamo riscrivere come
τi=miri2αi
Ora, sommiamo i momenti di tutte le particelle del corpo
rigido:
∑τ = ∑ m r α
2
i
i
i i
i
i
_________________________________________________________________________________________________
15
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Al secondo membro, imponiamo il modello del corpo
rigido richiedendo che tutte le particelle abbiano la
stessa accelerazione angolare α. Quindi, questa
equazione diventa

2
∑τ =  ∑ m r
i i
i
α

Dove il momento e l’accelerazione angolare non hanno
più i pedici poiché si riferiscono a grandezze associate al
corpo rigido nel suo insieme piuttosto che a singole
particelle.
∑τ = Iα
Cioè, il momento risultante delle forze agenti su un corpo
rigido è proporzionale alla sua accelerazione angolare, e
la costante di proporzionalità è il momento d’inerzia. E’
importante notare che Στ = Iα è l’analogo rotazionale
della seconda legge del moto di Newton, ΣF = ma.
_________________________________________________________________________________________________
16
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Consideriamo inizialmente una particella di massa m,
posta nella posizione r e che si muova con una quantità
di moto p. Il momento angolare istantaneo L della
particella rispetto all’origine O è definito come il prodotto
vettoriale del vettore posizione istantanea r e del vettore
quantità di moto istantanea p:
r r r
L ≡ r xp
_________________________________________________________________________________________________
17
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
La direzione di L è perpendicolare al piano individuato
da r e p, e il suo verso è determinato dalla regola della
mano destra. Il modulo di L è dato da
L = mvrsenφ
dove φ è l’angolo tra r e p. Ne segue che L è zero
quando r è parallelo a p (φ = 0° o 180°). In altre parole
quando una particella si muove lungo una retta
passante per l’origine, essa ha momento angolare nullo
rispetto all’origine.
_________________________________________________________________________________________________
18
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Se r è perpendicolare a p (φ = 90°), L è massimo e
uguale a mvr.
Iniziamo scrivendo il momento della forza agente sulla
r
particella nella forma
r
r
r
r dp
dt
τ = r xF = r x
Deriviamo poi rispetto al tempo, seguendo la regola
della derivata del prodotto:
r
r
r
dL d r r r dp dr r
= (r xp ) = r x +
xp
dt dt
dt dt
E’ importante seguire l’ordine dei fattori nel prodotto
vettoriale poiché esso non è commutativo.
_________________________________________________________________________________________________
19
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
L’ultimo termine del secondo membro della precedente
equazione è nullo poiché v = dr/dt è parallelo a p.
r
r
Quindi,
dL r dp
= rx
dt
dt
Dal confronto, si ha
r
dL
τ =
dt
r
Immaginiamo un corpo rigido che ruota attorno a un
asse. Ciascuna particella di massa mi del corpo rigido si
muove di moto circolare di raggio ri, con velocità
tangenziale vi. Quindi, il momento angolare totale del
corpo rigido è
L = ∑ mi vi ri
i
_________________________________________________________________________________________________
20
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Sostituiamo la velocità tangenziale con il prodotto della
distanza radiale per la velocità angolare:


L = ∑ mi vi ri = ∑ mi (riω )ri =  ∑ mi ri 2 ω
i
i
 i

Riconosciamo la quantità fra parentesi come il
momento d’inerzia, cosicché possiamo scrivere il
momento angolare del corpo rigido come
L = Iω
Che è l’analogo rotazionale di p = mv.
_________________________________________________________________________________________________
21
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Il momento angolare totale di un sistema resta costante
se il momento risultante delle forze esterne agenti sul
r
sistema è nullo.
r
dLtot
∑τ est = dt = 0
Allora
r
r
r
Ltot = cos t → Ltot ,i = Ltot , f
_________________________________________________________________________________________________
22
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Un dischetto di massa m che si trova su un tavolo
orizzontale privo di attrito è collegato a una fune che
passa attraverso un piccolo foro nel tavolo. Il dischetto
viene messo in rotazione su una traiettoria circolare di
raggio R con velocità di modulo vi.
a) Se la fune viene tirata dal basso in modo che il raggio
della circonferenza diminuisca fino a r, quale sarà la
velocità finale vf del dischetto?
mvi R = mv f r
_________________________________________________________________________________________________
23
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
b) In questo processo si conserva l’energia cinetica del
dischetto?
1 2
2
mv f
Kf
v
R
1
R2


i
2
=
= 
 = 2
1 2 vi2  r 
Ki
r
mvi
2
_________________________________________________________________________________________________
24
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier
Possiamo esprimere l’energia cinetica totale di un corpo
che rotola, di massa M e di momento d’inerzia I, come
la combinazione dell’energia cinetica di rotazione
attorno al centro di massa più l’energia cinetica di
traslazione del centro di massa:
K=
1
1
2
I CM ω 2 + MvCM
2
2
_________________________________________________________________________________________________
25
Lez. 13 - MOMENTO ANGOLARE
Giovanni Mettivier