Documentazione scuola sec II grado

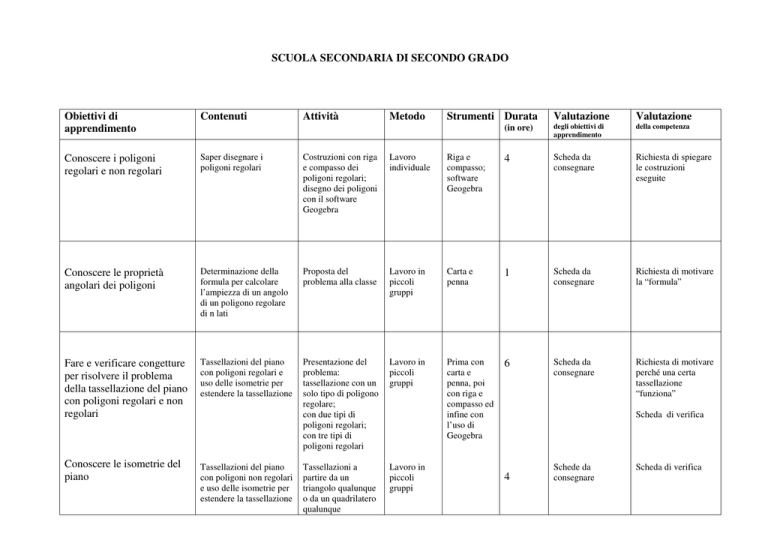
SCUOLA SECONDARIA DI SECONDO GRADO
Obiettivi di
apprendimento
Contenuti
Attività
Metodo
Conoscere i poligoni
regolari e non regolari
Saper disegnare i
poligoni regolari
Costruzioni con riga
e compasso dei
poligoni regolari;
disegno dei poligoni
con il software
Geogebra
Lavoro
individuale
Conoscere le proprietà
angolari dei poligoni
Determinazione della
formula per calcolare
l’ampiezza di un angolo
di un poligono regolare
di n lati
Proposta del
problema alla classe
Fare e verificare congetture
per risolvere il problema
della tassellazione del piano
con poligoni regolari e non
regolari
Tassellazioni del piano
con poligoni regolari e
uso delle isometrie per
estendere la tassellazione
Conoscere le isometrie del
piano
Tassellazioni del piano
con poligoni non regolari
e uso delle isometrie per
estendere la tassellazione
Strumenti Durata
Valutazione
Valutazione
(in ore)
degli obiettivi di
apprendimento
della competenza
Riga e
compasso;
software
Geogebra
4
Scheda da
consegnare
Richiesta di spiegare
le costruzioni
eseguite
Lavoro in
piccoli
gruppi
Carta e
penna
1
Scheda da
consegnare
Richiesta di motivare
la “formula”
Presentazione del
problema:
tassellazione con un
solo tipo di poligono
regolare;
con due tipi di
poligoni regolari;
con tre tipi di
poligoni regolari
Lavoro in
piccoli
gruppi
Prima con
carta e
penna, poi
con riga e
compasso ed
infine con
l’uso di
Geogebra
6
Scheda da
consegnare
Richiesta di motivare
perché una certa
tassellazione
“funziona”
Tassellazioni a
partire da un
triangolo qualunque
o da un quadrilatero
qualunque
Lavoro in
piccoli
gruppi
Scheda di verifica
4
Schede da
consegnare
Scheda di verifica
Sintesi dell’attività
Scuola secondaria di secondo grado
La sperimentazione relativa alla secondaria di secondo grado è stata effettuata nella classe 1B del
liceo delle scienze applicate dell’I.S.I.S “B. Varchi” di Montevarchi (composta da 31 studenti) nel
periodo Febbraio-Marzo 2014 dalla prof.ssa Cecilia Magni (insegnante di matematica della classe)
lavorando con cadenza settimanale.
Inizialmente sono state riprese, insieme all’insegnante di disegno e storia dell’arte, le costruzioni
con riga e compasso dei poligoni regolari e si è discusso su come determinare l’ampiezza
dell’angolo di un poligono regolare di n lati.
Successivamente nel laboratorio di informatica è stato introdotto l’uso del software Geogebra per
disegnare i poligoni ed applicare ad essi le principali isometrie.
E’ stato poi posto alla classe, divisa in piccoli gruppi di lavoro, il seguente problema:
“Con quali poligoni regolari è possibile ricoprire esattamente il piano?”
Si è lasciato in un primo momento che i gruppi lavorassero come volevano (la maggior parte hanno
fatto disegni “a mano libera”): dalla discussione collettiva e dalla considerazione del fatto che in
ogni vertice la somma degli angoli dovesse essere 360° è emerso che alcune delle tassellazioni
trovate erano sicuramente corrette mentre altre erano errate.
Per dare un po’ di ordine al lavoro l’insegnante ha chiesto di concentrarsi prima sulle tassellazioni
con un solo tipo di poligono regolare, poi su quelle con due tipi e infine con tre tipi di poligoni
regolari , facendo inoltre in modo che tutti i vertici fossero dello stesso “tipo” cioè che vi
convergesse lo stesso numero e tipo di poligoni (vedi attività n°1).
Dopo aver provato a “mano libera” e poi con riga e compasso, gli studenti hanno utilizzato il
software Geogebra e pian piano sono state scoperte tutte le tassellazioni (3 con un solo tipo di
poligono, 6 con due tipi di poligoni e 2 con tre tipi di poligoni regolari diversi) (vedi lavori allegati).
Alcuni studenti hanno anche colorato i poligoni per ottenere un effetto “artistico”.
.
Poi è stato posto il problema:
“Si può tassellare il piano con un triangolo qualunque? E con un quadrilatero qualunque?”
Per il triangolo la soluzione è stata trovata facilmente da tutti i gruppi mentre nel caso del
quadrilatero solo alcuni gruppi sono riusciti a risolvere il problema (per guidare il lavoro, dopo la
discussione, sono state proposte le schede di lavoro 2 e 3).
Molto importante è stato anche rendersi conto (utilizzando la funzione “muovi” del software) che le
tassellazioni con triangoli equilateri e quadrati si ottenevano come caso particolare.
E’ stata anche asegnata una verifica riguardante la tassellazione con un particolare pentagono.
Infine è stato proposta la realizzazione di “tassellazioni artistiche” (vedi allegati): partendo da un
poligono con cui si può tassellare il piano (triangolo equilatero , quadrato, rettangolo ecc.) e su cui è
stato aggiunto un piccolo disegno, si è chiesto agli studenti di costruire (utilizzando le isometrie)
“pavimenti” diversi (abbiamo anche fatto una piccola ricerca sulle bellissime decorazioni presenti
nell’Alhambra di Granada).
In conclusione direi che il problema proposto e il metodo di lavoro in piccoli gruppi è stato
stimolante per gli studenti che hanno sempre partecipato con entusiasmo alle attività proposte.
Inoltre gli obiettivi di apprendimento sono stati raggiunti per la maggior parte degli studenti e
l’aspetto sicuramente più formativo dell’attività è stato senza dubbio quello di poter fare congetture
e metterle alla prova con l’uso di Geogebra.
ATTIVITA’ 1
Tassellazioni con poligoni regolari
Con quali poligoni regolari possiamo “ricoprire” perfettamente il piano facendo coincidere lato con
lato e vertice con vertice?
“Tassellazioni” con un solo tipo di poligono regolare
Se usiamo solo un tipo di poligono regolare quali sono quelli con cui posso “tassellare” il piano?
Fai le tue congetture e verificale con Geogebra.
Suggerimento: l’angolo interno di un triangolo equilatero misura 60°, l’angolo interno di un
quadrato misura 90°…….
Stampa le tue “tassellazioni” con un solo tipo di poligono regolare.
Nota
Una volta capito quali poligoni regolari puoi usare, per ricoprire il piano puoi utilizzare traslazioni,
rotazioni, simmetrie assiali ….
Indica quali isometrie hai utilizzato per “estendere” la tua tassellazione.
“Tassellazioni” con due tipi di poligoni regolari
Se possiamo usare come “mattonelle” della nostra pavimentazione due tipi di poligoni regolari quali
sono le combinazioni che funzionano?
Scrivi una tabella con il valore degli angoli interni dei vari poligoni regolari…
Suggerimento: quadrato con triangolo equilatero dovrebbe funzionare e forse ci sono anche più
modi di sistemare le “mattonelle” intorno ad un vertice…
Ci sono altre combinazioni?
Stampa le tassellazioni che sei riuscito a trovare con due tipi di poligoni regolari.
“Tassellazioni” con tre tipi di poligoni regolari
E se possiamo usare tre tipi diversi di poligoni regolari?
Stampa le tassellazioni che sei riuscito a costruire.
ATTIVITA’ 2
Tassellazione con un triangolo qualunque
Possiamo tassellare il piano partendo da un triangolo qualunque?
Prova a fare così:
disegna un triangolo qualunque con il comando poligono, costruisci il punto medio M di un suo lato
e applica la simmetria centrale rispetto a M del triangolo.
Hai ottenuto così un parallelogramma con cui puoi “tassellare” il piano (basta traslare secondo i lati
del parallelogramma). Stampa la tua tassellazione.
Per evitare che vengano messe tutte le etichette ai vertici puoi selezionare Opzioni – etichettatura –
nessun nuovo oggetto.
E’ interessante provare a “muovere” i vertici del triangolo per modificarlo: si può ritrovare in
questo modo anche la tassellazione con i triangoli equilateri che avevamo già individuato.
Possiamo anche divertirci a colorare i vari triangoli (tasto destro – proprietà – colore – scelta del
colore – aumentare l’opacità ) per avere un effetto “artistico” : possiamo per esempio colorare i
primi due e oi applicare le traslazioni….
ATTIVITA’ 3
Tassellazione con un quadrilatero qualunque
Possiamo tassellare il piano con un quadrilatero qualunque?
Prova a fare così: disegna un quadrilatero qualunque con il comando poligono, costruisci il punto
medio M di un lato, effettua la simmetria di centro M del quadrilatero.
Hai ottenuto un esagono che tassella il piano con traslazioni corrispondenti alle diagonali del
quadrilatero iniziale!
Osservazione
E’ interessante notare che in ogni vertice della tassellazione si ritrovano i quattro angoli del
quadrilatero iniziale e che perciò la loro somma è proprio 360°.
Inoltre non è importante quale lato si sceglie per costruire il punto medio e fare la prima simmetria
centrale: partendo da un altro lato si sarebbe ottenuto lo stesso risultato (i quadrilateri accostati
risultano sempre simmetrici rispetto al punto medio del loro lato in comune).
ATTIVITA’ 4
Partendo da una “mattonella”… pavimenti diversi!
Partendo da un poligono che tassella il piano, per esempio un quadrato, e disegnandovi sopra un
“fregio” (vedi figura) possiamo utilizzare le isometrie per ottenere pavimenti diversi!
Per esempio se semplicemente trasliamo la mattonella otteniamo il primo “pavimento”, se facciamo
una simmetria rispetto ad un lato e poi trasliamo otteniamo il secondo “pavimento”, se ruotiamo la
mattonella intorno ad un vertice per 4 volte di 90°e poi trasliamo otteniamo il terzo “pavimento”….
Prova a partire da una “mattonella triangolo-equilatero” e costruisci pavimenti diversi!
Scheda di verifica
Abbiamo visto che non è possibile ricoprire il piano con pentagoni regolari poiché l’angolo interno
di un pentagono regolare misura 108° che non è divisore di 360°.
Ma ci sono pentagoni con cui è possibile ricoprire il piano?
Prova a tassellare il piano con un pentagono irregolare con due lati uguali che formano un angolo di
60° e due lati uguali che formano un angolo di 120°.
Per prima cosa disegnalo:
•
•
•
costruisci un segmento AB, costruisci un angolo di 60° di vertice A (il comando “angolo di
data misura” costruisce automaticamente un punto B’ tale che AB=AB’);
costruisci un segmento BC e fai un angolo BCB1 ' =120° : attenzione poiché il comando
angolo di data ampiezza costruisce l’ angolo in senso antiorario dobbiamo digitare 240°;
con il comando poligono riprendi i vari punti e chiudi il pentagono.
A questo punto prova a “tassellare” il piano!
Stampa la tua tassellazione….magari puoi anche colorarla...
Quali isometrie hai usato per creare la tua tassellazione?
Esempi di elaborati degli studenti
Attivita’ 1
Tassellazioni con un solo tipo di poligono regolare
Tassellazioni con due tipi di poligoni regolari
Tassellazioni con tre tipi di poligoni regolari
Tassellazioni in cui i vertici non sono tutti dello stesso “tipo”
Attivita’ 2
Attivita’ 3
Attivita’ 4
Scheda di verifica