vol1_blu_rec_18 1..7

Scheda
18
Scheda per il recupero 18
A Ripasso
Quadrilateri
Trapezi e parallelogrammi
DOMANDE
RISPOSTE
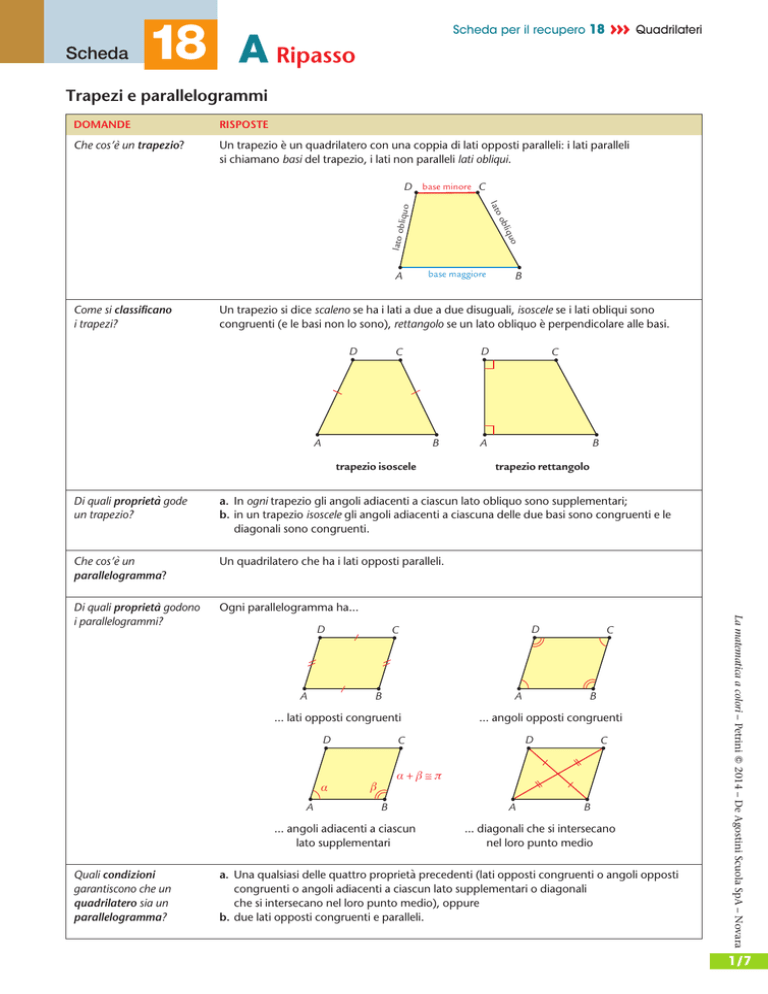
Che cos’è un trapezio?
Un trapezio è un quadrilatero con una coppia di lati opposti paralleli: i lati paralleli
si chiamano basi del trapezio, i lati non paralleli lati obliqui.
D base minore C
Come si classificano
i trapezi?
o
iqu
lato ob
li
obl
quo
lato
A
base maggiore
B
Un trapezio si dice scaleno se ha i lati a due a due disuguali, isoscele se i lati obliqui sono
congruenti (e le basi non lo sono), rettangolo se un lato obliquo è perpendicolare alle basi.
D
D
C
A
B
trapezio isoscele
C
A
B
trapezio rettangolo
a. In ogni trapezio gli angoli adiacenti a ciascun lato obliquo sono supplementari;
b. in un trapezio isoscele gli angoli adiacenti a ciascuna delle due basi sono congruenti e le
diagonali sono congruenti.
Che cos’è un
parallelogramma?
Un quadrilatero che ha i lati opposti paralleli.
Di quali proprietà godono
i parallelogrammi?
Ogni parallelogramma ha...
D
A
B
A
... lati opposti congruenti
D
α
A
C
B
... angoli opposti congruenti
D
C
C
α+β≅π
β
B
... angoli adiacenti a ciascun
lato supplementari
Quali condizioni
garantiscono che un
quadrilatero sia un
parallelogramma?
D
C
A
B
... diagonali che si intersecano
nel loro punto medio
a. Una qualsiasi delle quattro proprietà precedenti (lati opposti congruenti o angoli opposti
congruenti o angoli adiacenti a ciascun lato supplementari o diagonali
che si intersecano nel loro punto medio), oppure
b. due lati opposti congruenti e paralleli.
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
Di quali proprietà gode
un trapezio?
1/7
Scheda
18
Scheda per il recupero 18
A Ripasso
Quadrilateri
Parallelogrammi particolari
Rettangolo
DEFINIZIONE
PROPRIETÀ
FIGURA
Un quadrilatero con i quattro
angoli retti.
Le diagonali sono congruenti.
D
A
Rombo
Un quadrilatero con i quattro
lati congruenti.
C
B
AC ≅ BD
D
Le diagonali sono:
perpendicolari;
bisettrici degli angoli
interni al rombo.
A
C
B
Quadrato
Un quadrilatero con i quattro
lati congruenti e i quattro
angoli retti.
C
D
Le diagonali sono congruenti,
perpendicolari e bisettrici
degli angoli interni al
quadrato.
A
AC ≅ BD
B
Attenzione!
Dalle definizioni di rettangolo, rombo e quadrato, segue immediatamente che tutti questi quadrilateri sono parallelogrammi.
Sai giustificarlo?
Piccolo teorema di Talete e teorema dei punti medi
A PAROLE
... di Talete
(piccolo)
Dato un fascio di rette parallele
tagliato da due trasversali, a
segmenti congruenti su una
trasversale corrispondono
segmenti congruenti sull’altra
trasversale.
IN SIMBOLI
A'
A
B'
B
C'
C
D'
D
r
... dei punti
medi
AB ffi CD
+
A0 B0 ffi C 0 D0
s
A
Il segmento che congiunge i
punti medi di due lati di un
triangolo è parallelo al terzo lato
e congruente alla sua metà.
M
B
N
C
AM ffi MB
AN ffi NC
) MN k BC, MN ffi
1
BC
2
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
TEOREMA
2/7
Scheda
18
Scheda per il recupero 18
B Verifica delle conoscenze
Quadrilateri
Vero o falso?
1
ogni parallelogramma ha le diagonali congruenti
V
F
2
un parallelogramma con tre angoli congruenti è un rombo
V
F
V
F
3 dato un parallelogramma ABCD, comunque scelto un punto P interno al lato CD, il quadrilatero ABPD
è un trapezio
4
un quadrilatero con gli angoli opposti congruenti è un parallelogramma
V
F
5
un quadrilatero con le diagonali perpendicolari è un rombo
V
F
6
un quadrilatero con un angolo retto e i lati opposti paralleli è un rettangolo
V
F
7
un quadrilatero che ha i quattro lati congruenti è un rombo
V
F
8
un quadrilatero con le diagonali congruenti è un rettangolo
V
F
9
se due lati consecutivi di un parallelogramma sono congruenti, allora il parallelogramma è un rombo
V
F
10 tutti i quadrati sono rombi
V
F
11 tutti i parallelogrammi sono rettangoli
V
F
12 se un parallelogramma ha un angolo retto, allora è un rettangolo
V
F
Completa.
13 Un quadrilatero che ha due lati opposti paralleli si chiama
:::::::::::::::::::::::::.
Se le diagonali di un tale quadrilatero sono
congruenti, allora esso si chiama ::::::::::::::::::::::::::::::::::::::::::::::::::.
14 Un quadrilatero che ha entrambe le coppie di lati opposti paralleli si chiama ::::::::::::::::::::::::::::::.
15 Un parallelogramma che ha un angolo retto è un ::::::::::::::::::::::::::::::::::::::::::::::::::.
16 Un rombo è un parallelogramma che ha ::::::::::::::::::::::::::::::::::::::::::::::::::.
17 Un quadrilatero che appartiene sia all’insieme dei rombi sia all’insieme dei rettangoli è un ::::::::::::::::::::::::::::::::::::::::::::::::::.
criterio di congruenza.
19 In un quadrilatero ABCD risulta AB ffi CD. Formula almeno due ipotesi aggiuntive, ciascuna delle quali, unita all’ipotesi AB ffi CD, garantisca che il quadrilatero sia un parallelogramma.
Ipotesi aggiuntiva 1: ::::::::::::::::::::::::::::::::::::::::::::::::::
Ipotesi aggiuntiva 2: ::::::::::::::::::::::::::::::::::::::::::::::::::
20 In un quadrilatero ABCD risulta AD k BC. Formula almeno due ipotesi aggiuntive, ciascuna delle quali, unita all’ipotesi AD k BC, garantisca che il quadrilatero sia un parallelogramma.
Ipotesi aggiuntiva 1: ::::::::::::::::::::::::::::::::::::::::::::::::::
Ipotesi aggiuntiva 2: ::::::::::::::::::::::::::::::::::::::::::::::::::
Test
21 Sia P l’insieme dei parallelogrammi; R l’insieme dei rettangoli; O l’insieme dei rombi; Q l’insieme dei quadrati. Quale delle seguenti relazioni non è corretta?
A
PR
B
RP
C
R\O¼Q
D
R[P ¼P
22 Sia P l’insieme dei parallelogrammi; R l’insieme dei rettangoli; O l’insieme dei rombi; Q l’insieme dei quadrati. Qua-
le delle seguenti relazioni non è corretta?
A
QP
B
R\P ¼R
C
Q[O¼O
D
RO
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
18 I due triangoli in cui un parallelogramma ABCD resta diviso da una diagonale sono congruenti in base al
::::::::::::::::::::::::::::::::::::::::::::::::::
3/7
Scheda
18
C Esercizi guidati
Scheda per il recupero 18
Quadrilateri
Sia ABCD un trapezio isoscele, di base maggiore AB e base minore CD. Sia P il punto d’intersezione dei prolungamenti dei lati obliqui del trapezio, PM la mediana relativa ad AB del triangolo APB e N il punto in cui PM interseca DC.
1
P
a. Il triangolo APB è isoscele perché :::::::::::::::::::::::::::::::::::::::::::::::::: .
b. Si può affermare che gli angoli DPbN e CPbN sono congruenti?
No
Sı̀, perché ::::::::::::::::::::::::::::::
c. Si può affermare che i due triangoli PND e PNC sono congruenti?
Sı̀, in base al ::::::::::::::::::::::::: criterio
No
d. In base al passo precedente, puoi dedurre che:
N è il punto medio di CD
P, N e M non sono allineati
N è il punto medio di PM
nessuna delle precedenti
2
N
D
A
C
M
B
Nella figura qui a fianco: AC ffi BC, PQ k AC e QR k AB.
a. In base alle ipotesi, il triangolo ABC è isoscele: su quale base? ::::::::::::::::::::
A
b. Dal fatto che ABC è isoscele (per ipotesi), che cosa si può dedurre?
bQ
bR ffi RC
PA
bQ
P BbQ ffi RC
bR ffi P BbQ
PA
R
P
c. Puoi affermare che il quadrilatero APQR è un parallelogramma?
Si, perché . . .. . .. . .. . .. . .. . .. . ...
No, le ipotesi non sono sufficienti
b R?
bR ffi P Q
d. Puoi affermare che P A
Q
B
C
Sı̀, perché lati opposti di un parallelogramma
Sı̀, perché angoli corrispondenti rispetto a due rette parallele tagliate da una trasversale
No, le ipotesi non sono sufficienti
bR?::::::::::::::::::::
e. In base alle deduzioni dei passi precedenti, che cosa puoi dedurre degli angoli P BbQ e PQ
3 Nella figura qui a fianco, il quadrilatero ABCD è un parallelogramma, AK ? CD e CH ? AB. Considera i triangoli
AKD e CHB.
a. Completa, giustificando perché gli elementi indicati sono congruenti:
b B perché ::::::::::::::::::::::::::::::::::::::::
AKbD ffi CH
bK ffi H BbC perché ::::::::::::::::::::::::::::::::::::::::
AD
AD ffi BC
D
K
C
A
H
perché ::::::::::::::::::::::::::::::::::::::::
b. In base a quale criterio si può affermare che AKD e CHB sono congruenti?
4
Secondo
Terzo
Nella figura qui a fianco, il quadrilatero ABCD è un trapezio.
B
C
D
a. Sapendo che AM ffi MD, che cosa si può affermare in base al teorema di Talete?
AB ffi 2CD
N è il punto medio di CB
b. Rispetto a quali rette parallele e a quali trasversali si è applicato tale teorema?
B
A
Parallele: AB, MN e CD; trasversali: AD e BC
Parallele: AB e CD; trasversali: AD e BC
Trasversali: AB, MN e CD; parallele: AD e BC
Parallele: AD e BC; trasversali: AB e CD
5
N
M
AD ffi BC
Nella figura qui a fianco:
il quadrilatero ABCD è un parallelogramma;
M e N sono, rispettivamente, i punti medi di DC e AB;
P e Q sono due punti, il primo appartenente ad AD e il secondo appartenente a BC.
O è il punto d’intersezione di PQ e MN.
a. Si può affermare che ANMD è un parallelogramma. Per quale ragione?
Perché, per ipotesi, ha i lati opposti congruenti
Perché, dalle ipotesi, segue che i lati ::::::::::::::: e ::::::::::::::: sono congruenti e paralleli
D
C
M
P
O
A
Q
N
B
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
Primo
Secondo generalizzato
4/7
Scheda
18
C Esercizi guidati
Scheda per il recupero 18
Quadrilateri
Perché, per ipotesi, ha i lati opposti paralleli
Per nessuna delle ragioni precedenti
Di conseguenza AD k :::::::::::::::
b. Analogamente si può affermare che :::::::::::::::::::: è un parallelogramma. Di conseguenza MN k :::::::::::::::
c. Considera le tre rette AD, MN e BC (parallele per quanto osservato in a. e in b.) e le due trasversali PQ e AB. In base
al teorema di Talete, che cosa puoi dedurre dei segmenti PO e OQ? ::::::::::::::::::::
6
Completa la seguente tabella in cui ti guidiamo a svolgere una dimostrazione.
Passi
È dato un parallelogramma ABCD. Costruisci, nel semipiano di origine DC opposto a quello in
cui giace ABCD, un parallelogramma DCFE. Dimostra che ABFE è un parallelogramma.
Figura
E
F
C
D
B
A
Ipotesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Tesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Dimostrazione
Poiché ABCD è un parallelogramma:
AB ffi ::::::::::
e AB k ::::::::::
Poiché DCFE è un parallelogramma:
DC ffi ::::::::::
e DC k ::::::::::
Per la proprietà :::::::::::::::::::::::::::::: della congruenza e del parallelismo puoi dedurre che:
AB ffi ::::::::::::::: e AB k :::::::::::::::
Ma allora il quadrilatero ABFE ha i lati opposti ::::::::::::::::::::::::: e ::::::::::::::::::::, quindi ::::::::::::::::::::.
7
Completa la seguente tabella in cui ti guidiamo a svolgere una dimostrazione.
Passi
Sia ABC un triangolo isoscele sulla base AB e CH l’altezza relativa ad AB. Indica:
Dimostra che AP 0 ffi P 0 H ffi HQ 0 ffi Q 0 B.
Figura
C
P
A
P'
Q
H Q' B
Ipotesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Tesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Dimostrazione
Per il teorema di Talete puoi affermare che:
AP 0 ffi :::::::::: e HQ 0 ffi ::::::::::
L’altezza relativa alla base di un triangolo isoscele è anche :::::::::::::::, quindi AH ffi ::::::::::::::: .
Di conseguenza :::::::::::::::::::::::::::::: .
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
con P e Q, rispettivamente, i punti medi di AC e BC;
con P 0 e Q 0 , rispettivamente, le proiezioni di P e Q su AB.
5/7
Scheda
8
18
Scheda per il recupero 18
C Esercizi guidati
Quadrilateri
Completa la seguente tabella in cui ti guidiamo a svolgere una dimostrazione.
Passi
b e indica con P il suo punto
In un parallelogramma ABCD, traccia la bisettrice dell’angolo A
b e indica con Q il suo punto
d’intersezione con CD. Poi traccia la bisettrice dell’angolo D
d’intersezione con AB. Dimostra che il quadrilatero AQPD è un rombo.
P
D
Figura
A
Q
C
B
Ipotesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Tesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Dimostrazione
Osserviamo che:
bP
DPbA ffi Q A
in quanto angoli :::::::::::::::::::: rispetto alle
rette parallele :::::::::: e ::::::::::, tagliate dalla trasversale :::::::::: .
bP ffi ::::::::::
QA
per ipotesi
Dunque, per la proprietà :::::::::::::::::::: della congruenza:
DPbA ffi ::::::::::
Pertanto il triangolo ADP è isoscele sulla base :::::::::::::::::::: e quindi:
AD ffi ::::::::::
[*]
Ragionando in modo analogo si deduce che il triangolo ADQ è :::::::::::::::::::: sulla base
::::::::::, quindi:
AD ffi ::::::::::
[**]
Da [*] e [**], segue che ::::::::::::::::::::; d’altra parte è anche AQ k :::::::::: quindi il quadrilatero
AQPD è un ::::::::::::::::::::::::::::::. Tale parallelogramma è un rombo perché ::::::::::::::::::::::::::::::::::::::::.
9
Completa la seguente tabella in cui ti guidiamo a svolgere una dimostrazione.
Passi
Dimostra che congiungendo i punti medi dei lati di un rombo si ottiene un rettangolo.
C
Figura
R
Q
B
S
P
A
Ipotesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Tesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Dimostrazione
I punti R e Q sono i punti medi dei lati DC e BC del triangolo DBC, quindi:
1
RQ k :::::::::: e RQ ffi ::::::::::
2
Ragionando analogamente possiamo dedurre che:
SP k :::::::::: e SP ffi ::::::::::
RS k :::::::::: e RS ffi ::::::::::
QP k :::::::::: e QP ffi ::::::::::
Queste relazioni dicono in particolare che i lati RQ e SP sono paralleli alla diagonale
:::::::::::::::::::: mentre i lati RS e QP sono paralleli alla diagonale ::::::::::::::::::::. Poiché in un
rombo le diagonali sono :::::::::::::::::::::::::::::::::::, puoi dedurre che :::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: .
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
D
6/7
Scheda
18
Scheda per il recupero 18
D Esercizi da svolgere
1 Un rombo è un quadrilatero con le diagonali perpendicolari. Non è vero, invece, che ogni quadrilatero
con le diagonali perpendicolari è un rombo. Disegna nella
figura un controesempio.
Quadrilateri
8 Dimostra che un rombo con un angolo retto è un
quadrato.
9 Sia ABCD un rombo e sia O il punto d’intersezione
delle diagonali. Indica con H, K, R e S le proiezioni di O,
rispettivamente, sui lati AB, BC, CD e AD. Dimostra che:
a. H, O e R sono allineati;
c. HKRS è un rettangolo.
b. K, O e S sono allineati;
10 Sia ABCD un trapezio rettangolo, di base maggiore
AB e base minore CD, con angoli retti in A e in D. Indica
con M il punto medio del lato obliquo BC. Dimostra che
MA ffi MD.
(Suggerimento: traccia l’altezza relativa ad AD del triangolo
AMD)
2 Un rettangolo è un quadrilatero con le diagonali
congruenti. Non è vero, invece, che ogni quadrilatero
con le diagonali congruenti è un rettangolo. Disegna nella
figura un controesempio.
11 Considera un trapezio e traccia il segmento che
congiunge i punti medi dei suoi lati obliqui. Dimostra
che tale segmento è parallelo alle basi del trapezio e dimezza le diagonali.
12 In un trapezio isoscele ABCD, di base maggiore AB e base minore CD, sia M il punto medio di CD e N il punto medio
di BD. Dimostra che MN è congruente alla metà di AD.
13 Dimostra che congiungendo i punti medi dei lati di
un rettangolo si ottiene un rombo.
3 In un trapezio ABCD, di base maggiore AB e base
minore CD, traccia la bisettrice dell’angolo ABbC e indica
con E il punto in cui interseca la retta CD. Dimostra che
BC ffi EC.
TESI:
ABCD è un parallelogramma
A
B
15 Dimostra che un quadrilatero con due lati opposti
congruenti e paralleli e le diagonali congruenti è un rettangolo.
5 Dato un segmento PQ, di punto medio M, traccia
due rette p e q, passanti rispettivamente per P e Q, parallele tra loro. Una retta r, passante per M, interseca p in R e q
in S. Dimostra che PSQR è un parallelogramma.
16 Dimostra che congiungendo i punti medi dei lati
obliqui di un trapezio isoscele con il punto medio di una
delle due basi, si ottiene un triangolo isoscele.
Sia ABCD un parallelogramma e siano M, N, P e Q i
punti medi di AB, BC, CD e AD. Dimostra, nell’ordine,
che:
17 Sia ABC un triangolo isoscele sulla base AB. Indica
con P e Q, rispettivamente, i punti medi dei lati obliqui
AC e BC e con P 0 , C 0 , Q 0 le proiezioni di P, C e Q su AB.
Dimostra che 2P 0 Q 0 ffi AB.
6
a. AMQ e CNP sono congruenti;
b. PDQ e MBN sono congruenti;
c. QM k PN.
Considera un triangolo ABC, isoscele sulla base AB.
Traccia la bisettrice dell’angolo esterno di vertice C del
triangolo e indica con D il punto d’intersezione della retta cui appartiene tale bisettrice con la retta passante per B
e per il punto medio di AC. Dimostra, nell’ordine, che:
7
a. la bisettrice è parallela al lato AB;
b. il quadrilatero ABCD è un parallelogramma.
18 Dimostra che il quadrilatero che ha per vertici i
punti medi dei lati di un trapezio isoscele è un rombo.
19 Sia ABCD un parallelogramma. Indica con P il punto d’intersezione delle bisettrici degli angoli adiacenti alla
base AB e dimostra che APbB è retto.
20 Sia ABC un triangolo isoscele sulla base AB. Prolunga AC, dalla parte di C, di un segmento CE e BC, dalla parte di C, di un segmento CD congruente a CE. Dimostra
che ABED è un trapezio isoscele.
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
Sulla diagonale AC di un parallelogramma ABCD,
considera due punti P e Q tali che AP ffi QC. Dimostra
che PBQD è un parallelogramma.
4
14 In riferimento alla figura sotto, scrivi l’enunciato
del teorema la cui ipotesi e la cui tesi sono quelle indicate
e dimostralo.
bB ffi DBbC
IPOTESI: AD ffi BC e AD
D
C
7/7