Il processo di carica e di scarica del condensatore
R
1
R
2
ε
2
Vin
i(t )
C
A
i(t )
VC
VC
C
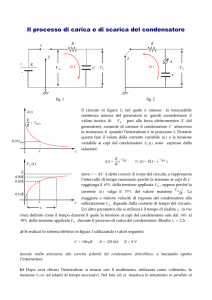
fig. 1
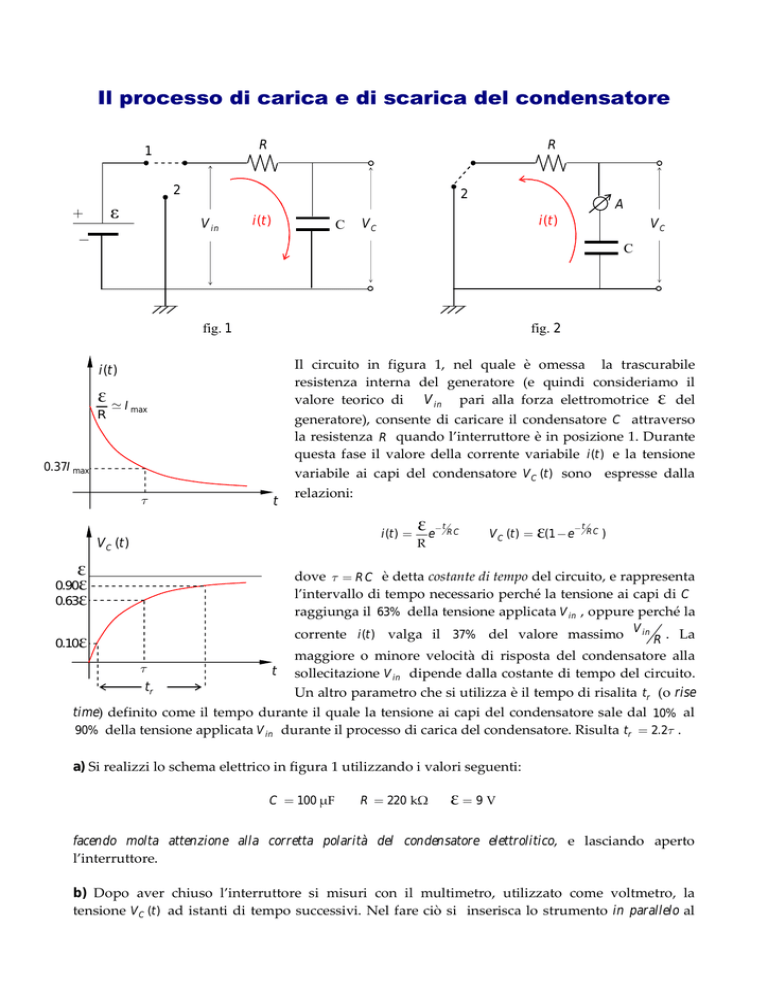
fig. 2
Il circuito in figura 1, nel quale è omessa la trascurabile
resistenza interna del generatore (e quindi consideriamo il
valore teorico di Vin pari alla forza elettromotrice ε del
i(t )
ε I
R
max
generatore), consente di caricare il condensatore C attraverso
la resistenza R quando l’interruttore è in posizione 1. Durante
questa fase il valore della corrente variabile i(t ) e la tensione
0.37I max
variabile ai capi del condensatore VC (t ) sono espresse dalla
t
relazioni:
i(t )
VC (t )
ε
0.90ε
0.63ε
ε e t RC
R
VC (t ) ε(1 e
t RC
)
dove RC è detta costante di tempo del circuito, e rappresenta
l’intervallo di tempo necessario perché la tensione ai capi di C
raggiunga il 63% della tensione applicata Vin , oppure perché la
ε
0.10
tr
t
corrente i(t ) valga il 37% del valore massimo Vin R . La
maggiore o minore velocità di risposta del condensatore alla
sollecitazione Vin dipende dalla costante di tempo del circuito.
Un altro parametro che si utilizza è il tempo di risalita tr (o rise
time) definito come il tempo durante il quale la tensione ai capi del condensatore sale dal 10% al
90% della tensione applicata Vin durante il processo di carica del condensatore. Risulta tr 2.2 .
a) Si realizzi lo schema elettrico in figura 1 utilizzando i valori seguenti:
C 100 µF
R 220 kΩ
ε9 V
facendo molta attenzione alla corretta polarità del condensatore elettrolitico, e lasciando aperto
l’interruttore.
b) Dopo aver chiuso l’interruttore si misuri con il multimetro, utilizzato come voltmetro, la
tensione VC (t ) ad istanti di tempo successivi. Nel fare ciò si inserisca lo strumento in parallelo al
condensatore C , stando attenti alla scelta del fondo scala, sapendo che ci attendiamo un valore di
tensione dello stesso ordine di grandezza di quello teorico VC (t ) ε(1 e
t RC
) . Considerato che la
costante di tempo di questo circuito vale:
RC 220 103 100 106 22 s
converrà leggere i valori della tensione dapprima scandendo in intervalli di tempo brevi, (ad
esempio ogni 5 s ), allo scopo di campionare bene la veloce fase di salita iniziale della curva.
Successivamente, quando la crescita si fa più dolce, le letture di tensione potranno essere diradate
ad istanti multipli della costante di tempo ( 2 , 3 , 4 e così via).
b) Si costruisca la tabella:
t [s ]
VC (t ) teorica
VC (t ) misurata
i(t ) teorica
imis (t )
ε VC (t )mis
R
e si rappresenti graficamente l’andamento di VC (t ) misurata in funzione del tempo. Dal grafico si
desumano i valori della costante di tempo e del tempo di risalita, e si confrontino le misure con i
valori teorici RC , tr 2.2RC .
c) Con l’interruttore aperto, ed il condensatore così carico, si inserisca in serie al condensatore il
multimetro usato come amperometro, interrompendo opportunamente il circuito. Dopo aver
calcolato l’ordine di grandezza atteso per la corrente di scarica tramite la formula teorica,
i(t )
ε e t RC ,
R
si imposti un adeguato fondo scala sullo strumento. Si porti quindi l’interruttore in
posizione 2 affinché il condensatore si scarichi attraverso la resistenza R e si eseguano misure
della corrente di scarica con lo stesso criterio di scansione dei tempi di lettura del punto b).
d) Si costruisca la tabella:
t [s ]
i(t ) teorica
i(t ) misurata
VR (t )teo
VR (t )mis Ri(t )mis
e si rappresenti graficamente l’andamento di i(t ) misurata in funzione del tempo sullo stesso
diagramma del precedente ma con una seconda scala sull’asse delle ordinate.
e) Si stimi l’area sottesa dalla curva misurata di
i(t ) per mezzo della somma delle aree dei
ε
R
rettangoli di base t ed altezza i(t )mis . Sapendo
che tale area eguaglia la carica Q
complessivamente accumulata sul condensatore:
i(5 s)
i(10 s)
Q
i(t)dt εC
0
si effettui una misura del valore di C e la si
confronti con quello realmente utilizzato.
i(3 )
5 s 10 s
…
3
4
5