Variabili Casuali - Brigantaggio.net

Variabili Casuali
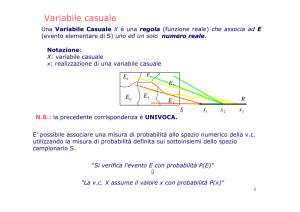
Variabile Casuale
Una variabile casuale è una funzione a valori
reali definita su uno spazio degli eventi,
quindi una funzione che associa agli
elementi dello spazio Ω degli eventi un
numero reale
Variabili Casuali
Discrete
Variabili Casuali
Continue
1
Variabile Casuale Discreta
La v.c. X è detta discreta se assume un
numero finito o una infinità numerabile di
valori x1, x2, ..xk
La funzione che associa ai valori x1, x2, ..xk
le rispettive probabilità P(X=xi), i=1,…,k
si chiama distribuzione di probabilità ed è
tale per cui
k
∑ P( X = xi ) = 1
i =1
Variabile Casuale Continua
Una v.c continua è una funzione che può assumere tutti i valori
compresi in un intervallo (a,b)
{
}
La funzione x, f ( x )
x
P( X ≤ x) =
∫
−∞
f ( ⋅) ≥ 0 è detta densità di frequenza
è tale per cui
con
f ( u ) du e
∞
∫ f ( u ) du = 1
−∞
dove P( X ≤ x) rappresenta l’area sotto la curva
f ( ⋅)
fino al punto x, cioè la funzione di ripartizione.
Per le variabili casuali continue P(X=x)=0, i casi possibili sono di
Per le variabili casuali continue P(X=x)=0, i casi possibili sono di
fatto infiniti e quindi
fatto infiniti e quindi
# casi favorevoli 1
P ( X = xi ) =
= =0
∞
# casi possibili
2
Esercizio:
Si considerino due dadi a 3 facce e sia X la variabile casuale ‘somma dei
due dadi’
• Si costruisca la variabile casuale X
• Si calcolino E(X) e V(X)
Ω = {(1,1)(1, 2 )(1, 3 )( 2,1)( 2, 2 )( 2, 3 )( 3,1)( 3, 2 )( 3, 3 )}
2
3
4
xi
ni
pi
2
3
4
5
6
1
2
3
2
1
9
1/9=0.11
2/9=0.22
3/9=0.33
2/9=0.22
1/9=0.11
1
3
4
5
4
5
6
∑ xi pi = 2 ⋅ 0.11 + 3 ⋅ 0.22 + .... = 4
2
V ( X ) = ∑ xi2 p i − [ E ( X ) ] =
E(X ) =
(
)
= 2 2 ⋅ 0.11 + 3 2 ⋅ 0.22 + .... − 4 2 = 1, 33
Esperimento Bernoulliano
E’ esperimento casuale che consiste in un insieme di n prove ripetute
con le seguenti caratteristiche:
i)
Ad ogni singola prova si hanno solo due esiti possibili, ‘successo’
e ‘insuccesso’
ii) La probabilità p di ‘successo’ è costante
iii) Le prove sono indipendenti
n =1
Variabile Casuale di Bernoulli
n >1
Variabile Casuale Binomiale
3
Variabile Casuale di Bernoulli
Variabile casuale discreta che assume solo 2 valori 0 e 1 con
probabilità rispettivamente (1-p) e p con 0<p<1 è detta variabile
casuale di Bernoulli. Si scrive
X ≈ Ber ( p )
Proprietà:
P ( X = 1) = p; P ( X = 0) = 1− p 0 < p < 1
E ( X ) = p; V ( X ) = p (1− p)
Variabile Casuale Binomiale
La Variabile casuale discreta che conta il numero di successi in n prove
bernoulliane dove p , 0<p <1, è la probabilità di successo nella singola
prova è detta variabile casuale Binomiale. Si scrive X ≈ Bin ( n , p ) e
assume tutti i valori interi da 0 a n secondo la seguente distribuzione di
probabilità
n
n− x
P ( X = x) =   p x (1 − p )
 x
x = 0,1,..., n
Proprietà:
E
(X ) =
n p ; V ( X ) = n p (1 − p )
Ad ogni prova le condizioni sono uguali a quelle di partenza, cioè p è costante
Ad ogni prova le condizioni sono uguali a quelle di partenza, cioè p è costante
4
ESEMPIO: VARIABILE CASUALE BINOMIALE
Dato un mazzo di 52 carte, si estraggano 5 carte con rimessa e si
consideri la variabile
X=“n° carte di cuori”
a) Che variabile è?
b) Probabilità di estrarre 3 cuori?
c) Probabilità di estrarre almeno 3 cuori?
d) Probabilità di estrarre al più 3 cuori
e) Probabilità di non estrarre cuori
f)
Probabilità di estrarre almeno 1 cuori
ESEMPIO: VARIABILE CASUALE BINOMIALE
a) Che variabile è?
13 

X ≈ Bin  n = 5, p =  ⇒ X ≈ Bin ( 5, 0.25 )
52 

b) Probabilità di estrarre 3 cuori?
 5
5!
3
5−3
P ( X = 3) =   ( 0.25) (1 − 0.25) =
0.2530.752 = 0.088 8,8%
3!2!
 3
c) Probabilità di estrarre almeno 3 cuori?
P ( X = 3) + P ( X = 4) + P ( X = 5) =
 5
3
2  5
4
1  5
5
0
=   ( 0.25) (1 − 0.25) +   ( 0.25) (1 − 0.25) +   ( 0.25) (1 − 0.25) =
 3
 4
 5
= 0.088 + 0.0146 + 0.001 = 0.1036 10,36%
5
ESEMPIO: VARIABILE CASUALE BINOMIALE
d) Probabilità di estrarre al più 3 cuori
P ( X = 0 ) + P ( X = 1) + P ( X = 2 ) + P ( X = 3 ) =
= P ( X ≤ 3 ) = 1 − P ( X > 3 ) = 1 −  P ( X = 4 ) + P ( X = 5 )  =
= 1 − [ 0 .0 1 4 6 + 0 .0 0 1 ] = 0 .9 8 4 9 8 , 4 %
e) Probabilità di non estrarre cuori
P
(X
5
0
5
= 0 ) =   ( 0 . 2 5 ) (1 − 0 . 2 5 ) = 0 . 2 3 7 3
0
2 3 ,7 3 %
f) Probabilità di estrarre almeno 1 cuori
P
=
( X = 1)+ P ( X
P ( X ≥ 1) = 1 −
= 2)+ P
P
(X
<
= 1 − 0 .2 3 7 3 = 0 .7 6 2 7
(X = 3)+ P (X = 4)+
1) = 1 − P ( X = 0 ) =
P
(X
= 5)=
76,27%
ESERCIZIO: VARIABILE CASUALE BINOMIALE
7 amici lanciano 2 monete ciascuno. Calcolare la probabilità che 2 di essi ottengano 2
teste.
Soluzione
Detta X la variabile casuale “numero di teste” si osserva che tale variabile si distribuisce
secondo la legge binomiale cioè: X ≈ Bi (7; p )
essendo 7 il numero dei giocatori.
Si pone ora il problema di determinare la probabilità p dell’evento “coppia di teste per un
giocatore”. Anche in questo caso si tratta di una legge binomiale, quella che descrive
l’esperimento casuale “numero di teste per un giocatore” ovvero Y ≈ Bi(2;0.5)
essendo 2 il numero di monete lanciate da ogni giocatore ed essendo 0.5 la probabilità
che ogni moneta mostri il lato con la “testa”.
Quindi:
p => Pr {Y = 2} = 0 .25
e quindi
P r {"2 am ici o tten g o no 2 teste"} = P r { X = 2 } = 0 .3 11 46 2
6