La statistica nella ricerca scientifica Pubblicazione dei risultati ® Presentazione dei dati e la loro elaborazione devono seguire criteri universalmente validi Impossibile verifica dei risultati da parte di altri studiosi ® raccolta dati non corretta, loro presentazione inadeguata ed analisi statistica non appropriata La metodologia statistica rappresenta uno strumento indispensabile per lo studio, l’interpretazione e la divulgazione delle informazioni contenute nei dati sperimentali La metodologia statistica fornisce un criterio oggettivo alla spiegazione del fenomeno
Come è organizzata la metodologia statistica?
La ricerca sperimentale procede secondo le seguenti fasi: Osservazione del fenomeno Formulazione dell’ipotesi Sperimentazione Campionamento Permette di raccogliere i Raccolta dati dati in funzione dello Discussione scopo della ricerca Accettazione o rifiuto dell’ipotesi Disegno sperimentale Permette che le osservazioni in natura e le ripetizioni in laboratorio sono scelte e programmate in funzione della ricerca e delle ipotesi esplicative e non casuali Descrizione Insieme delle tecniche utilizzate per la sintesi dei dati grezzi in parametri statistici (media, deviazione standard, ecc.) Utilizzazione del test statistico Processo logico­matematico che, mediante il calcolo di probabilità specifiche, porta alla conclusione di non o poter respingere l’ipotesi della casualità Principi e definizioni Popolazione: totalità degli individui aventi in comune almeno un carattere Variabile: caratteristiche di una popolazione che può essere misurata 1. Variabile qualitativa: generate da risposte categoriali (es. con un test sulla tossicità, le cavie muoiono o sopravvivono; con un farmaco, i pazienti guariscono o rimangono ammalati; ecc.); 2. Variabile quantitativa: risultato di risposte numeriche ( es., per un’analisi del dimorfismo animale, le dimensioni dell’organo o il peso dei maschi e delle femmine) 2A. Variabile Discreta: assume solo valori isolati 2B. Variabile Continua: tutti i valori di un intervallo Parametro: stima delle caratteristiche della popolazione Es. la lunghezza del fusto è di 10 cm Lunghezza ® variabile 10 cm ® parametro
Campione: parte della popolazione Fattore: elemento, antropico o naturale, esterno alla popolazione che modifica in maniera più o meno evidente i parametri della popolazione. Es., l’irrigazione, la concimazione, la tessitura del suolo, ecc. Livelli: i livelli ai quali i fattori sono testati Es., dose di fertilizzante, diversi gradi di tessitura, ecc. Trattamenti: il livello o la combinazione di più livelli di uno o più fattori applicato ad un’unità sperimentale. Es. 0, 10 e 20 Kh/ha di azoto: Azoto ® Fattore Dose fertilizzante ® Livello 0, 10 e 20 Kg/ha ® Trattamenti
Unità sperimentale: è un’unità di materiale sperimentale alla quale è stato applicato un trattamento. Es., individuo, una pianta o un’intera parcella Replica: è un’unità sperimentale ripetuta 1 replica Unità sperimentale Unità sperimentale Unità sperimentale 2 replica 3 replica
0 Kg/ha Azoto 0 Kg/ha Azoto 0 Kg/ha Azoto 10 Kg/ha azoto 10 Kg/ha azoto 10 Kg/ha azoto 20 Kg/ha azoto 20 Kg/ha azoto 20 Kg/ha azoto Parametro statistico: indice che riassume sinteticamente una o più varianti del campione. Es. media, moda, deviazione standard, ecc. Inferenza: estensione dei risultati del campione alla totalità della popolazione Statistica descrittiva: Insieme delle tecniche utilizzate per la sintesi dei dati grezzi in pochi indici informativi (Es. metodologia per il calcolo della media, della deviazione standard, ecc.) Statistica inferenziale: insieme dei metodi con cui si possono elaborare i dati dei campioni per dedurne omogeneità o differenze nelle caratteristiche analizzate, al fine di estendere le conclusioni alla popolazione
Studio di un insieme di dati La sperimentazione porta all’ottenimento di una serie di dati non organizzati Nessun giudizio sulle ipotesi formulate “ E’ necessario organizzare i dati in modo sintetico e condensato” criterio di organizzazione dei dati: distribuzione per classi di frequenza Esempio: consideriamo 50 osservazioni di altezza di sorgo da fibra
Raggruppamento per frequenza Raggruppamento per classi di frequenza e frequenza relativa (numero di individui della classe/numero totale d’individui) Formula per calcolo numero di classi K = 1 + 3.322 log n K: numero di classi n: numero osservazioni
Rappresentazion e grafica Vantaggi Presenta la totalità delle informazioni Svantaggi A) l’insieme non è chiaro ® presentare sotto forma più breve e più chiara B) l’insieme non si presta a calcoli né a rigorosi confronti ® occorre trasformarlo “ Non è efficace” Un parametro statistico è più efficace: 1) quanto meglio riassume il contenuto informativo dei dati iniziali con la minor perdita di informazioni (sintetico) 2) quanto meglio si presta ai calcoli ed ai test ulteriori (numerico e trasformabile)
2° criterio di organizzazione dei dati: la media La media aritmetica (m) è ottenuta dividendo la somma dei valori per il numero dei casi Es. consideriamo le seguenti tre serie di misure: A: 99, 100, 101 (media = m = 100) B: 90, 100, 110 (media = m = 100) C: 1, 100 ,199 (media = m = 100) Risultato: la media da sola non è in grado di fornire una sufficiente informazione sul campione da cui è estratta. E’ necessario considerare la dispersione di valori attorno alla media cioè la variabilità del set di dati La variabilità può essere espressa in diversi modi: 1. Intervallo di variazione: differenza tra il valore massimo e minimo; 2. Devianza o scarto quadratico medio: somma delle singole distanze dalla media elevate al quadrato 3. Varianza (s 2): rapporto tra la devianza ed il numero delle osservazioni meno 1 (gdL) 4. Deviazione standard (s): radice quadrata della varianza; 5. Coefficiente di variazione (CV): rapporto tra la deviazione standard e la media il tutto per 100
Esempio: calcolare la media, la varianza e la deviazione standard delle produzioni parcellari di frumento (Kg) Totali valori Scarti Quadrati degli scarti 18,2 18,2 ­ 20,3 = ­2,1 4,41 22,2 22,2 ­ 20,3 = 1,90 3,61 18,7 18,7 ­ 20,3 = ­1,60 2,56 22,6 22,6 ­ 20,3 = 2,3 5,29 19,8 19,8 ­ 20,3 = ­0,5 0,25 101,5 0 16,12 Numero osservazioni (n) = 5 Gradi di libertà: numero osservazioni meno uno (n­1) = 5­1=4 Soluzione
1. Media (m) = 101,5 Kg 2. Varianza (s 2 ) : somma quadrati degli scarti/ Gradi libertà 16,12 / 4 = 4,03 3. Deviazione standard (s): √Varianza √4,03 = 2,0074 Che cosa significa “ gradi di libertà” I gradi di libertà sono “ la quantità di dati necessaria alla stima di un parametro, ossia il numero di dati indipendenti” Matematicamente corrispondono al numero delle osservazioni meno 1 Consideriamo l’esempio precedente valori Scarti Quadrati degli scarti 18,2 18,2 ­ 20,3 = ­2,1 4,41 22,2 22,2 ­ 20,3 = 1,90 3,61 18,7 18,7 ­ 20,3 = ­1,60 2,56 22,6 22,6 ­ 20,3 = 2,3 5,29 19,8 19,8 ­ 20,3 = ­0,5 0,25 101,5 0 16,12 La somma degli scarti è uguale a 0 Se non è indipendente significa che la sua informazione è già contenuta implicitamente negli altri dati
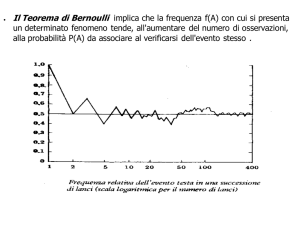
Per poter determinare la somma dei quadrati degli scarti è sufficiente disporre di tutti gli scarti meno uno poiché quest’ultimo è ricavabile per differenza (cioè non è indipendente) Distribuzione normale: relazioni campione ­ popolazione I parametri statistici, media, varianza e deviazione standard, fin qui discussi sono relativi ad un campione, poiché teoricamente è impossibile determinare tali parametri per un’intera popolazione Fino a quale punto i dati raccolti su un campione permettono di stimare le caratteristiche della popolazione di origine? Per dare una risposta a tale domanda facciamo il percorso inverso: partiamo dalle caratteristiche della popolazione per arrivare a quelle del campione L’esperienza ha dimostrato che le variabili biologiche quantitative di una popolazione sono “ distribuite normalmente”
Che significa “ distribuite normalmente” ? Distribuzione del peso di 175 topi Distribuzione del peso di un numero elevatissimo di topi In una popolazione normalmente distribuita si ha un addensamento dei valori attorno ad una frequenza massima ed una dispersione simmetrica che declina man mano che ci si allontana dai valori centrali. Tipica curva a campana o di Gauss
Caratteristiche della curva di Gauss Media 1. è simmetrica rispetto ad un asse 2. l’asse di simmetria coincide con la media 3. le distanze misurate a partire dalla media sono le deviazioni standard La media della popolazione (m) è diversa di quella del campione La deviazione standard della popolazione (s) è diversa di quella del campione
Quanto si scosta la media di un campione da una media della popolazione? Studi matematici hanno calcolato la probabilità che un campione preso a caso dalla popolazione presenta un valore medio (m) compreso entro certi limiti La probabilità di estrarre un campione che abbia 1) una media uguale a quella della popolazione ± 1s è del 68% m = m ±1s ® 68%; Conclusioni: 1. a partire da un campione estratto da 2) una media uguale a quella della popolazione ± 2s è del 95,44% m = m ± 2s ® 95,44%; una popolazione, è impossibile calcolare esattamente i parametri m e s; 2. è invece possibile stimare i loro valori 3) una media uguale a quella della popolazione ± 3s è del 99,73% m = m ±3s ® 99,73%; più probabili che sono la media del campione (m) e la deviazione standard (s)
Teorema del limite centrale “ Se una popolazione è distribuita normalmente con una media m ed una deviazione standard s, le medie (m 1 , m 2 , …., m n ) di un numero infinito di campioni, ciascuno composto da n individui estratti a caso dalla popolazione si distribuiscono secondo la curva di distribuzione normale la cui media è uguale a m e la deviazione standard è uguale a s/√n” Il valore s/√n viene definito deviazione standard della media o errore standard (s m , SE Dai dati di un campione è possibile inferire sulla popolazione : 1. m±1sm ha il 67% delle probabilità di contenere la media della popolazione 2. m±1sm ha il 95% delle probabilità di contenere la media della popolazione 3. m±1sm ha il 99% delle probabilità di contenere la media della popolazione
Conclusioni pratiche 1. Una serie di misurazioni devono essere considerati come n individui di un campione la cui media (m) e deviazione standard (s) rappresentano la migliore stima della media (m) e deviazione standard (s) della popolazione da cui il campione è estratto; 2. L’estrazione del campione deve essere casuale; 3. Una serie di campioni ognuno aventi n individui ed estratti da una popolazione, hanno una media m ed una deviazione standard pari a s/√n che è l’errore standard
Statistica inferenziale: il confronto fra campioni In precedenza Confronto fra un singolo campione e una popolazione 2 1 Confronto fra due campioni: 1. Fanno parte della stessa popolazione? 2. Fanno parte di popolazioni diverse? Praticamente Si stabilisce, scelto un arbitrario livello di probabilità, se due campioni trattati in maniera diversa siano significativamente differenti tra loro
Risultati significativi e non­significativi Conoscere con chiarezza 1) le convenzioni abitualmente usate nell’applicazione dei test statistici e 2) alcune nozioni teoriche fondamentali nell’inferenza. Test statistico: procedure che, sulla base di dati campionari e con un certo grado di probabilità, consente di decidere se è ragionevole respingere l’ipotesi nulla H 0 oppure non esistono elementi sufficienti per respingerla. Ipotesi nulla o H 0 : gli effetti osservati nei campioni sono dovuti a fluttuazioni casuali 1. Se l’H O è accettata ® i campioni non sono significativamente differenti: appartengono alla stessa popolazione; 2. Se l’H O non è accettata ® i campioni sono significativamente differenti: appartengono a popolazioni differenti; La scelta delle ipotesi (H 0 ) è fondata sulla probabilità di ottenere per caso il risultato osservato nel campione nella condizione che l’ipotesi nulla sia vera. Quanto più tale probabilità è piccola, tanto più è improbabile che H 0 sia vera.
La probabilità dipende dal valore stimato con il test o indice statistico (P) L’insieme di valori ottenibili con il test formano la distribuzione campionaria dell’indice statistico (P) e può essere diviso in due zone: 1. la zona di rifiuto dell’ipotesi nulla (regione critica), che corrisponde ai valori collocati agli estremi della distribuzione; quelli che hanno una probabilità piccola di verificarsi per caso; 2. la zona di accettazione dell’ipotesi nulla, che comprende i restanti valori Se il valore dell’indice statistico cade nella zona di rifiuto, si respinge l’ipotesi nulla Per convenzione, i livelli di soglia delle probabilità sono tre: 0.05 (5%), 0.01 (1%) e 0.001 (0.1%)
Confronto tra due medie con il test di t Student Assunzioni: A. I campioni provengono da popolazioni distribuite normalmente B. le rispettive varianze siano omogenee (omoscedasticità) Quando si utilizza? 1. per il confronto della media di un campione (media osservata) con una generica media attesa
Soluzione:
3 One­sample t test of VAR1 with 7 cases; Ho: Mean = 25.00000 Mean = 23.00000 SD = 1.73205 95.00% CI = 21.39812 to 24.60188 t = ­3.05505 df = 6 Prob = 0.02237 Con probabilità inferiore a 0.05 (di commettere un errore) si rifiuta l’ipotesi nulla, cioè le differenze non sono dovute al caso Count 2 1 0 20 21 22 23 24 VAR1 25 Praticamente: Le sostanze tossiche disperse inibiscono la crescita delle piante della specie A in modo significativo 26 One­sample t test of VAR1 with 13 cases; Ho: Mean =1.25000 10 Count Mean = 1.23538 99.00% CI=1.18579 to 1.28498 SD= 0.05854 t = ­0.90018 df = 12 Prob = 0.38573 15 5 0 1.1 1.2 1.3 1.4 VAR1 Con probabilità inferiore a 0.01 (di commettere un errore) si accetta l’ipotesi nulla, cioè le differenze sono dovute al caso Praticamente: La dimensione media dei 13 individui della specie Hetrocypris incongruens pescati nel fiume, non è significativamente diversa da quella degli individui della stessa specie che vivono nei laghi della regione.
2. Confronto tra le medie di due campioni indipendenti 2A. Confronto tra un campione di individui sottoposti a trattamento ed un altro campione di individui che servono come controllo (non trattato) Test unilaterale o ad una coda: il test dirà se una media è superiore ad un’altra escludendo a priori che essa possa essere minore. O viceversa, ma solamente l’una o l’altra. 2B. Confronto tra le medie di due trattamenti diversi Test bilaterale o a due code: hanno significato tutte le teoriche possibili risposte. Questo test stabilisce se le due medie sono differenti Entrambi i test si possono attuare sia con campioni indipendenti o appaiati sia su campioni dipendenti o non appaiati
Sono campioni dipendenti o appaiati quando un’osservazione di un campione si accoppia ad una sola osservazione dell’altro campione Esempio 3 Osservare che i dati sono appaiati La sostanza può essere la causa di variazioni significative di peso?
Paired samples t test on PRIMA vs DOPO with 10 cases Mean PRIMA = 168.20000 Mean DOPO = 177.40000 Mean Difference = ­9.20000 99.00% CI = ­18.13032 to ­0.26968 SD Difference = 8.68971 t = ­3.34798 df = 9 Prob = 0.00855 Prob = 0.00855 < 0.05 Si rifiuta l’ipotesi nulla in quanto la probabilità che la differenza riscontrata sia dovuta al caso è minore di 0.05 Praticamente: la nuova dieta determina nelle cavie una differenza ponderale significativa
Sono campioni indipendenti o dati non appaiati campioni formati da individui differenti. Quindi sono due gruppi di osservazioni ottenute in modo indipendente. Vantaggi: possono avere un numero differente di osservazioni e sono espressione della variabilità casuale Esempio 4
In questo caso i dati sono indipendenti
Gli animali cresciuti nella soluzione con concentrazione algale maggiore (gruppo X 1 ) hanno raggiunto dimensioni significativamente superiori a quelli cresciuti nella soluzione con concentrazione algale minore (gruppo X 2 ) ? Two­sample t test on VARIABL grouped by CONC$ Group N Mean SD X1 20 4.04430 0.12596 X2 20 3.05135 0.08995 t = 28.68940 df = 34.4 Prob = 0.00000 Difference in Means = 0.99295 95.00% CI = 0.92264 to 1.06326 VARIABL Separate Variance 5 Pooled Variance t = 28.68940 df = 38 Prob = 0.00000 Difference in Means = 0.99295 95.00% CI = 0.92289 to 1.06301 4 3 CONC 2 20 15 10 5 Count 0 5 10 15 20 Count X1 X2 Praticamente La maggior concentrazione algale influisce in modo altamente Prob = 0.00000 << 0.05 significativo sulla maggior crescita delle Daphnie
Si rifiuta l’ipotesi nulla in quanto la probabilità che la differenza riscontrata sia dovuta al caso è minore di 0.05 Esempio 5 Dati indipendenti e mancanza di un dato
Two­sample t test on PH grouped by ROCCE SD 0.12287 0.17727 Separate Variance t =16.17330 df = 21.4 Prob = 0.00000 Difference in Means = 0.98051 95.00% CI = 0.85458 to1.10644 9 8 PH Group N Mean X1 12 8.11667 X2 13 7.13615 7 ROCCE 6 15 10 5 Count 0 5 10 Count 15 X1 X2 Pooled Variance t =15.93822 df = 23 Prob = 0.00000 Difference in Means = 0.98051 95.00% CI = 0.85325 to 1.10778 Si rifiuta l’ipotesi nulla in quanto la probabilità che la differenza riscontrata sia dovuta al caso è minore di 0.05 Praticamente I due gruppi di laghi hanno un pH medio statisticamente molto diverso
Errore di I e II tipo In ogni confronto è possibile, per effetto del caso: 1. che venga considerato diverso (rifiuto dell’ipotesi nulla) ciò che in realtà non lo è (errore di tipo I o a) 2. che venga considerato simile (accettazione dell’ipotesi nulla) ciò che in realtà è differente (errore di tipo II o b) Non è possibile evitare tali errori, ma è possibile stabilire un limite massimo in cui il caso possa condurre a commettere errori Lo scarto di a dall’unità rappresenta il livello di protezione del test Esempio: con a=0.05, il livello di protezione è pari a 0.95 cioè al 95% delle probabilità Lo scarto di b dall’unità, rappresenta il livello di potenza del test cioè la capacità di evidenziare differenze
All’inizio di ogni test si stabiliscono i valori di a o b
Esempio nell’utilizzare diversi livelli di protezione e potenza del test Se si effettua una prova di pre­screening per individuare specie di probabile interesse per la produzione di biomassa, potrebbe essere utile abbassare il livello di protezione (a=0.1) a vantaggio di una maggiore potenza del test. Quindi, è meglio correre il rischio di includere specie che potrebbero essere inferiori, piuttosto che eliminare specie che potrebbero rivelarsi di estremo interesse La potenza del test 1. diminuisce all’aumentare di a 2. Aumenta se l’effetto del trattamento è maggiore 3. Aumenta se la varianza diminuisce (incremento del numero delle osservazioni)
Analisi della varianza (ANOVA) Nella ricerca sperimentale, il confronto avviene spesso simultaneamente tra più di due gruppi di individui “ Non è corretto ricorrere al test t Student per ripetere l’analisi tante volte quanti sono i possibili confronti a coppie tra i singoli gruppi” Perché ? Con il t test 1. si utilizza solo una parte dei dati 2. la probabilità a prescelta per l’accettazione dell’ipotesi nulla è valida solamente per ogni singolo confronto L’analisi della varianza consente di effettuare il confronto simultaneo tra più medie mantenendo invariata la probabilità a prefissata
Novità introdotta dall’ANOVA: Permette di scomporre e di misurare l’incidenza delle diverse fonti di variazione sui valori osservati di due o più gruppi Permette la ripartizione della varianza totale della variabile dipendente nella varie componenti attribuibili a fonti di variabilità nota (variabili indipendenti) e non nota (errore) Esempio Con il t test Per confrontare l’effetto di due tossici su un gruppo di cavie questi dovevano essere raggruppati il più omogeneo possibile. Cioè gli animali dovevano essere raggruppati per sesso, età, dimensione, ecc. Quindi, le conclusioni sono limitate al gruppo di animali con le caratteristiche prescelte, senza la possibilità di estensione ad altri caratteri. Per comprendere l’incidenza degli altri caratteri si doveva ripetere l’esperimento variando un carattere alla volta. Con l’ANOVA Conoscendo le cause ed i diversi fattori, è possibile attribuire ad ognuna di essi la parte di effetto determinata e contemporaneamente ridurre la variabilità d’errore. Quindi, posso testare contemporaneamente l’effetto dei diversi fattori e le loro interazioni: 1) sesso 2) età 3) dimensioni
Il giudizio di significatività viene dedotto dal rapporto tra varianza apportata dal trattamento (oggetto d’indagine) e quella dovuta ai fattori non controllabili (errore o varianza dovuta al caso). Tale rapporto (F oss ) viene poi confrontato con la distribuzione di F (statistica di Fisher) (F tab ) Se F oss ≥ a F tab , alla probabilità prefissata (a=0.05 o a=0.01) L’ipotesi nulla può essere rifiutata ® almeno una delle medie è diversa dalle altre
Assunzioni ’errore e le osservazioni devono essere distribuite normalmente ed indipendentemente 2. le varianze dei campioni devono essere omogenee (omoscedasticità) 3. le varianze dei campioni non sono correlate alle rispettive medie 4. gli effetti principali devono essere additivi
1A. Distribuzione normale ed indipendente dell’errore Procedura 1. Costruire la tabella degli errori: ad ogni dato si sottrae la media generale, quella del trattamento e quella del blocco (se è un disegno a blocchi randomizzati) 2. Osservare l’andamento dell’errore: es. errori differenti tra i trattamenti indicano non indipendenza L’errore è simile nei blocchi 1 e 4, e 2 e 3, per cui non è distribuito in modo randomizzato Soluzione: trasformazione dei dati
1B. Le osservazioni devono essere distribuite normalmente Test di Kolmogorv­Smirnov Test negativo: trasformazione dei dati 2. Le varianze dei campioni devono essere omogenee (omoscedasticità) Test Hartley Test Cochran Test Bartlett Test Levene Test Bartlett si utilizza quando ci sono dati mancanti Test Levene è preferibile in quanto è il più robusto Test negativi: trasformazione dei dati
Comunque per osservare che le varianze sono omogenee è bene controllare graficamente la distribuzione dell’errore sia prima del test sia dopo aver trasformato i dati 4. gli effetti principali devono essere additivi Test di Tukey Trasformazione dei dati La trasformazione dei dati stabilizza le varianze, normalizza le distribuzioni e linearizza i rapporti fra le variabili Esistono diversi tipi di trasformazione: logaritmica, esponenziale, ecc. Considerazioni per la scelta del tipo di trasformazione: 1. La logaritmica ® effetto moltiplicativo dell’errore o quando la varianza è correlata alla media 2. radice quadrata ® rende le varianze omogenee 3. reciproci ® efficace quando la varianza aumenta in modo molto pronunciato rispetto alla media 4. trasformazioni angolari ® dati in proporzioni o percentuali
Analisi della varianza a un criterio di classificazione (ANOVA I) Caratteristicihe 1 fattore a più livelli Esempio 6
Source Sum­of­Squares FATTORE$ Error df Mean­Square F­ratio 0.50294 2 0.25147 2.53815 P 0.12043 1.18890 12 0.09908 P > 0.05 per cui si accetta l’ipotesi nulla, cioè le differenze sono dovuta al caso Praticamente Le tre zone non mostrano differenze significative nella quantità in ferro
Confronti multipli o a posteriori Quando il confronto statistico avviene fra più di due campioni e l’ANOVA mostra differenze significative, confrontano le medie per conoscere quali gruppi sono significativamente differenti e quali no I confronti possono avvenire fra singole medie o fra gruppi di medie Cultivar X Cultivar Y 20 Kg/ha azoto 80 Kg/ha azoto Confronto 1 X20 X80 Y20 Y80 Confronto semplice 2 3 X Y 20 40 Confronto complesso