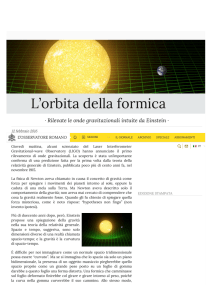
L’equazione dei campi gravitazionali di Einstein
a cura di Flavio Cimolin
(pagina a cura di Antonello Urso)
(ultimo aggiornamento: 22/10/2005)
Nel 1915 Albert Einstein trovò una generalizzazione della Relatività Ristretta applicabile a sistemi
di riferimento non inerziali (Relatività Generale). Lo spazio-tempo di Minkowski della Relatività
Ristretta infatti è incompatibile con l'esistenza della gravità. Un sistema di riferimento, che è
supposto inerziale per una particella situata lontano dalla Terra, in una regione dove il campo
gravitazionale è trascurabile, non sarà più inerziale quando la particella si troverà vicino alla Terra
Si può ottenere tuttavia una compatibilità approssimata tra i due sistemi a causa di una notevole
proprietà della gravitazione che prende il nome di principio di equivalenza: tutti i corpi di
dimensioni sufficientemente piccole che si trovano in un dato campo gravitazionale esterno cadono
con la stessa accelerazione, in modo indipendente dalla loro massa, e dalla loro composizione e/o
struttura.
Einstein per ricavare la sua formula fece uso della geometria di Riemann. L’equazione infatti
riporta al primo membro dei tensori (un tensore non è altro che un vettore con molteplici
componenti) di natura geometrica: due tensori di Riemann (indicati con la lettera R) che ci
forniscono informazioni sulla curvatura dello spazio, e il tensore metrico (indicato con la lettera g)
che ci fornisce informazioni sulla forma del tessuto spazio-temporale. Al secondo membro abbiamo
invece una costante χ per un tensore di natura fisica: il tensore energetico, che ci fornisce
informazioni sulla distribuzione nello spazio della massa e dell’energia. Quindi la formula non
esprime altro che il concetto: "Geometria = Fisica".
Una notevole conseguenza del principio di equivalenza è data dalla curvatura dello spazio-tempo:
se si pone una palla da bowling su un telone di gomma esso sprofonderà verso il basso intorno alla
palla, e le piccole biglie che prima si muovevano di moto rettilineo sopra il telone ora si
muoveranno di moto curvilineo, seguendo la curvatura del telone e saranno “attratte” verso la palla
di bowling. In altre parole, anziché attraverso un'interazione di tipo attrattivo in uno spazio piatto
come quello euclideo, Einstein viene ad interpretare la gravitazione come il moto inerziale delle
masse all'interno di un tessuto spazio-temporale incurvato, nel quale la geometria euclidea non vale
più. Due corpi quindi si attraggono solo per una proprietà geometrica, perché cioè deformano lo
spazio attorno a loro come per l’esempio della palla da bowling. Anche la luce segue allora nella
sua propagazione la curvatura dello spazio, e da questo Einstein dedusse che le grandi masse
devono essere in grado di attirare e di curvare anche i raggi di luce. La figura mostra la traiettoria di
http://www.matematicamente.it
Flavio Cimolin – L’equazione dei campi gravitazionali di Einstein
un fascio luminoso proveniente da una stella lontana che viene curvato dalla massa solare ed
intercettato da un osservatore sulla Terra.
La verifica sperimentale della deflessione dei raggi luminosi provenienti dalle stelle da parte del
Sole, ottenuta durante l'eclisse solare del 1919 rappresentò uno dei massimi trionfi della Relatività
Generale e procurò a Einstein una fama universale. Secondo la teoria, un raggio di luce che si
propaga attraverso lo spazio-tempo curvo in prossimità del Sole deve venire deflesso dalla sua
direzione iniziale di 1,75 secondi d'arco ogni volta che rasenta la superficie solare.
La teoria della Relatività Generale fu considerata per molto tempo un argomento di grande
impegno, adatto più per i matematici che per i fisici. Verso il 1960, tuttavia, cominciò a rinascere un
notevole interesse per la Relatività Generale, soprattutto a causa della scoperta di alcuni buchi neri
(che sono soluzioni particolari dell’equazione di Einstein) e la nascita di molteplici modelli
riguardanti la struttura delle stelle e dell’Universo. Oggi è considerata una branca di notevole
importanza dell’astrofisica e della cosmologia.
2
http://www.matematicamente.it