1. Definizioni e proprietà
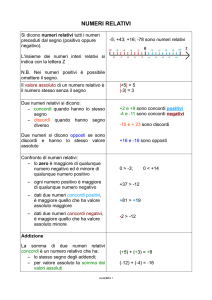
Numeri relativi: numeri il cui valore dipende dal segno che li precede.
+ 4 è un numero positivo, cioè maggiore di 0, perché preceduto dal segno “ + ”
(il segno + davanti ai numeri positivi è quasi sempre sottinteso: 4 vuol dire + 4)
- 3 è un numero negativo, cioè minore di 0, perché preceduto dal segno “ – “ .
Z = insieme degli interi : comprende numeri interi sia positivi che negativi .
Q = insieme dei razionali : comprende numeri razionali sia positivi che negativi
I = insieme degli irrazionali : comprende numeri irrazionali sia positivi che negativi
L'unione di Q e I forma l'insieme R dei numeri reali
REALI
Irrazionali
3,141592....
-1,414213....
Razionali
interi
1
-7
decimali
limitati
2 = 0,4
5
- 17 = -1,7
10
periodici
- 2 = -0,6
3
1 = 0,16
6
Valore assoluto o modulo: parte numerica senza considerare il segno.
Il valore assoluto si indica con “| | “ . Esempi : |+ 4| = 4 ; |-7|= 7
Numeri concordi: hanno stesso segno. Es. : + 3 e + 7; - 4 e - 6
Numeri discordi: hanno segno diverso. Es. : +2 e - 8
Numeri opposti: hanno segno diverso e stesso valore assoluto. Es. + 3 e -3
CONFRONTO DI NUMERI RELATIVI
1. Sulla retta dei numeri i negativi sono tutti a sinistra dello 0 e i positivi tutti a
destra dello 0. I numeri opposti sono da parti opposte rispetto allo 0.
2. Per confrontare tra di loro i numeri relativi devo ricordare che i numeri crescono
da sinistra verso destra: il numero minore è quello che sta più a sinistra.
Di conseguenza:
– ogni numero negativo è minore dello 0 e di tutti i numeri positivi: -20 < 0 < 17
– tra due numeri positivi è maggiore quello che ha valore assoluto maggiore: 76 > 22
– tra due numeri negativi è maggiore quello che ha valore assoluto minore: - 2 > - 17
2. LE QUATTRO OPERAZIONI FONDAMENTALI
Addizione e Sottrazione (Somma algebrica)
1. Numeri concordi: i valori assoluti si SOMMANO e il segno resta lo stesso
- 3 - 8 = - 11 ;
in pratica si calcola 3 + 8 e il segno resta -
+ 4 + 12 = + 16 ;
in pratica si calcola 4 + 12 e il segno resta +
2. Numeri discordi: i valori assoluti si SOTTRAGGONO e il segno è quello del numero
con il valore assoluto maggiore
-3+8=+5 ;
in pratica si calcola 8 - 3 e il segno è + perchè il valore assoluto
maggiore è del numero positivo + 8
+ 4 - 12 = - 8;
in pratica si calcola 12 - 4 e il segno è - perchè il valore assoluto
maggiore è del numero negativo - 12
NOTE:
1. tutte le eventuali proprietà delle operazioni (commutativa, associativa,
dissociativa, invariantiva) restano immutate.
2. le regole di sopra si applicano identiche per i numeri razionali.
es.
3 1 −3+2
1
− + =
=−
4 2
4
4
Moltiplicazione e Divisione
Il prodotto (o il quoziente) di due numeri relativi è un numero che ha:
– valore assoluto dato dal prodotto (o dal quoziente) dei valori assoluti
– segno + sei i due numeri sono concordi oppure segno – se i numeri sono discordi
Esempi:
concordi positivi:
(+ 5) x (+ 3) = + 15
(+ 15) : (+ 3) = + 5
concordi negativi:
(- 5) x (- 3) = + 15
(- 15) : (- 3) = + 5
discordi:
(- 5) x (+ 3) = (+ 3) x (- 5) = - 15
(- 15) : (+3) = (+15) : (-3)= - 5
Tabella riassuntiva:
x(:)
+
–
+
+
–
–
–
+
NOTE:
1. tutte le eventuali proprietà delle operazioni (commutativa, associativa,
dissociativa, distributiva, invariantiva) restano immutate
2. le regole di sopra si applicano identiche per i numeri razionali.
Esempi:
3 1 −3 ×1
3
− × =
=−
4 2 4 ×2
8
;
3 1
3
− 3× 2
6
− : =− ×2=
=−
4 2
4
4 ×1
4
3. PROPRIETA’ DISTRIBUTIVA DELLA MOLTIPLICAZIONE
1. RACCOGLIMENTO A FATTOR COMUNE
Da sinistra a destra → Proprietà distributiva
- 3 · (5 – 7 + 2 ) = ( -3 ) · 5 + (- 3) · (- 7) + (-3) · 2 = -15 + 21- 6 = 0
Da destra a sinistra ← Raccoglimento a fattor comune
esempio 1:
- 20 + 15 – 80 = (- 4 · 5) + (3 · 5) + (-16 · 5 ) = 5 · (- 4 + 3 – 16)
esempio 2:
13 + 21 – 7 = 13 · 1 + 3 · 7 + ( - 1 · 7) → Nessun fattore comune ai
tre numeri. Non si può
raccogliere.
2. USO DEI SEGNI E PARENTESI
Il “+ ” NON cambia i segni: quando ho il + davanti alle parentesi, posso eliminare le
parentesi e i segni dei numeri all'interno delle parentesi NON cambiano.
→ è una conseguenza della proprietà distributiva e delle regole della moltiplicazione:
davanti alla parentesi c'è il numero +1 che moltiplica i numeri nella parentesi
3 + ( + 4 – 2 + 7) = 3 + 1 x ( + 4 – 2 + 7 ) = 3 + 1 x (+ 4) + 1 x (- 2) + 1 x (+4) =
= 3 + 4 – 2 + 4 = + 12
Il “ - “ CAMBIA i segni: quando ho il – davanti alle parentesi, posso eliminare le
parentesi e i segni dei numeri all'interno delle parentesi SI INVERTONO.
→ è una conseguenza della proprietà distributiva e delle regole della moltiplicazione:
davanti alla parentesi c'è il numero -1 che moltiplica i numeri nella parentesi
3 – ( + 4 – 2 + 7) = 3 – 1 x ( + 4 – 2 + 7 ) = 3 + (-1) x (+ 4) + (-1) x (- 2) + (-1) x (+4) =
=3– 4 + 2 – 4=–5
4. POTENZA
ESPONENTE POSITIVO
Come conseguenza delle regole della moltiplicazione si ha che:
– base positiva → potenza sempre positiva
esempi: (+3)2 = (+ 3) · (+ 3) = + 9 ; (+2)3= (+2) · (+ 2) · (+ 2) = (+4) · (+ 2) = + 8
– base negativa → potenza positiva con esponente pari
→ potenza negativa con esponente dispari
esponente pari: (- 3)2= (-3) · (- 3) = + 9 ; (- 2)4 = (-2) · (- 2) · (- 2) · (- 2) = (+4) · (+ 4) = + 16
esponente dispari: (-3)3 = (-3) · (- 3) · (- 3)= (+9) · (- 3) = - 27
NOTE:
1. le proprietà delle potenze restano invariate.
2. le regole di sopra si applicano identiche per i numeri razionali.
es.
3 2
3
3
9
=− × − =
4
4
4 16
( ) ( )( )
−
3
3
3
3
3
9
3
27
= − × − × − = × − =−
4
4
4
4 16
4
64
( ) ( )( )( )
es.
−
( )
3. La radice quadrata di un numero positivo ammette due risultati opposti:
es.
√ 25=+5 o −5 perchè 5 ×5=25 e ( −5 ) × ( − 5 )=25
ESPONENTE NEGATIVO e NOTAZIONE SCIENTIFICA
Una potenza con base diversa da 0 e con esponente negativo si trasforma in una
potenza con base inversa ed esponente positivo.
Esempi:
3
4
−2
4 2 16
=
;
3
9
() ()
=
1
2
−3
( )
−
3
=( −2 ) =− 8 ;
4
( 2 )−4 = 1 = 1
2
16
()
1 3
1
10 =
=
=0,001
10
1000
−3
( )
Con l'ultimo esempio possiamo capire che la notazione scientifica può essere usata
non solo con potenze positive del 10 ma anche con potenze negative:
Esempi:
3.000.000 = 3 x 1.000.000 = 3 x 10 6
750.000 = 7,5 x 100.000= 7,5 x 10 5
1
= 3 x 10-6
1000000
0,000003 = 3 x 0,000001 =
3×
0,000075 = 7,5 x 0,00001=
3×
1
= 3 x 10-5
100000
NOTE:
→ ricorda che nella notazione scientifica il numero che moltiplica la potenza del 10
deve essere maggiore di uno e minore di 10!
→ le proprietà delle potenze restano valide anche con esponenti negativi
→ la notazione scientifica serve a fare i conti più velocemente:
0,000013 x 0,002 = 1,3 x 10 - 5 x 2 x 10 - 3 = 1,3 x 2 x 10 - 5 x 10 - 3 = 2,6 x 10
= 2,6 x 10 -5 - 3= 2,6 x 10
-8
- 5 + ( - 3)
=
TABELLA RIASSUNTIVA OPERAZIONI
OPERAZIONE
ADDIZIONE e
SOTTRAZIONE
REGOLA
ESEMPI
Segno: resta lo stesso
1) + 3 + 7 = + 10
Valori assoluti: si sommano
2) – 4 – 11 = – 15
NUMERI
CONCORDI
1 2 +5+ 6 + 11
=
3) + + =
3 5
15
15
5 3 − 10− 9
19
=−
4) − − =
9 6
18
18
ADDIZIONE e
SOTTRAZIONE
NUMERI
Segno: è quello del numero con
il valore assoluto maggiore
1) + 3 – 7 = – 4
2) – 5 + 12 = + 7
Valori assoluti: si sottraggono
3 1 + 9 −2 +7
=
3) + − =
4 6
12
12
DISCORDI
2 1 + 4 −5
1
=−
4) + − =
5 2
10
10
MOLTIPLICAZIONE Segno:
E
DIVISIONE
1) + 3 · (+ 7) = + 21 ; + 15 : (+ 3) = + 5
→ positivo se numeri concordi
2) – 2 · (– 5) = + 10 ; – 40 : ( – 5) = + 8
+ · +=+
; + : +=+
3) – 10 · (+ 3) = – 30 ; + 20 : (– 2) = – 10
- · -=+
; - : -=+
→ negativo se numeri discordi
+ · -=-
1
4
1
7
1× 7
7
=+
4) + : + =+ × + =+
3
7
3
4
3×4
21
( )
5)
; + : -=+
4
3
4
2
4×2
8
− : − =− × − =+
=+
5
2
5
3
5 ×3
15
( )
Valori assoluti: si moltiplicano o
dividono
6)
USO DEI SEGNI
Il “ + “ NON cambia i segni dei
numeri nelle parentesi
Il “ - “ INVERTE i segni dei
numeri nelle parentesi
( )
( )
2
1
2
2 ×5
2
− : + =− × ( +5 )=−
=−
3
5
3
3 ×1
15
( )
1) – 3 + ( – 5 + 4 – 7) = – 3 – 5 + 4 – 7 = – 11
2) – 3 – ( – 5 + 4 – 7) = – 3 + 5 – 4 + 7 = + 5
POTENZA
ESPONENTE
POSITIVO
base positiva → potenza
positiva
base negativa : 2 casi
1. esponente pari:
potenza positiva
2. esponente dispari: potenza
negativa
POTENZA
ESPONENTE
NEGATIVO
1) ( +2 )+3=( +2 ) × ( +2 ) × ( +2 )=+8
+1
3
+2
( ) =( +13 ) × ( +13 )= +19
2)
3) ( −2 )+2=( − 2 ) × ( −2 )=+ 4
4) ( −2 )+3=( − 2 ) × ( −2 ) × ( −2 ) =−8
Si trasforma in potenza con:
→ base INVERSA
→ esponente OPPOSTO
+3
( ) = +18
−3
+1
1) ( +2 ) =
2
3)
( )
−
1
5
=−
−2
2
3
+1
( ) ( ) =− 23
−
3
2
−1
2)
+2
=( −5 ) =+25