Assiomi per i numeri reali Gli assiomi [A1]

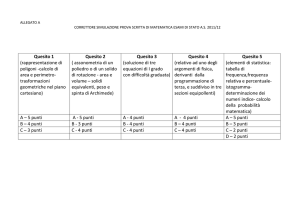
Assiomi per i numeri reali
Gli assiomi [A1]-[A5] relativi ad Addizione
Gli assiomi [M1]-[M5] relativi a Moltiplicazione
L’assiome [D] di Distributività di moltiplicazione rispetto addizione
Gli assiomi [O1]-[O4] di Ordine
L’assiome di Completezza: l’assiome del limite superiore
[
[
[
[
[
Elenco degli assiomi per R
I numeri reali R è un corpo ordinato completo, ossia essi sono caratterizzati dagli assiomi seguenti:
Assiomi di addizione
A1] Per ogni due elementi a, b ∈ R esiste un’operazione ben definita detto la loro “somma” ed indicata
da a + b.
A2] Per ogni terno a, b, c ∈ si ha a + (b + c) = (a + b) + c.
A3] Per ogni paio di elementi a, b ∈ R vale a + b = b + a.
A4] Esiste un elemento 0 ∈ R tale che per ogni a ∈ R vale a + 0 = a.
A5] Per ogni a ∈ R esiste un elemento (che si indica con −a) tale che
a + (−a) = 0.
Assiomi di moltiplicazione
Indichiamo con R\{0} la collezione di tutti gli elementi di R diversi da zero, ossia il complemento del
insieme {0} in R.
[ M1] Per ogni due elementi a, b ∈ R esiste un’operazione ben definita detto la loro “prodotto” ed indicata
da a · b (o spesso anche da ab).
[ M2] Per ogni terno a, b, c ∈ R vale a · (b · c) = (a · b) · c.
[ M3] Per ogni coppia a, b ∈ R vale a · b = b · a.
[ M4] Esiste un elemento 1 ∈ R tale che per ogni a ∈ R vale a · 1 = a.
[ M5] Per ogni a ∈ R\{0} esiste un elemento (che si indica con a−1 ) tale che
a · a−1 = 1.
Assiome di Distribuitiva di moltiplicazione rispetto ad addizione
[ D] Per ogni terno a, b, c di elementi di R vale a · (b + c) = a · b + a · c.
Assiomi di Ordine
[ O1 ] Su R si ha una relazione < tale che per ogni coppia a, b di elementi di R vale esattamente una
delle alternative seguenti: a ≤ b oppure a = b oppure b < a.
[ O2 ] Se a, b, c ∈ R e valgono sia a ≤ b che b ≤ c allora vale a ≤ c.
[ O3 ] Se a, b ∈ R ed a < b allora per ogni c ∈ R vale a + c < b + c.
[ O4 ] Se a, b ∈ R soddisfanno a < b e c ∈ R soddisfa 0 < c allora a · c < b · c.
Come si fa al solito si scrive a ≤ b per indicare che a < b oppure a = b.
Assiome di Completezza
[ Limite Superiore ] Se S è un sottoinsieme non-vuoto di R tale che esiste un elemento B ∈ R per cui
vale s ≤ B per ogni s ∈ S, allora esiste un elemento L di R tale che L è un limite superiore minimale
per S, cioè tale che
P er ogni s ∈ S si ha s ≤ L.
S e B ∗ è qualsiasi elemento di R tale che per ogni s ∈ S si ha s ≤ B ∗ allora B ≤ B ∗ .
1
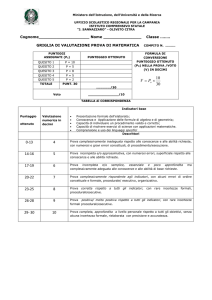
Analisi Matematica I
Esercizi per la prova scritta di 18-01-2010
Sia n1 n2 n3 n4 n5 n6 = N , il numero di matricola. (Esempio: se il numero di matricola è 534772, allora
n1 = 5, n2 = 3, n3 = 4, . . . , n6 = 2.
1.
Se n6 è pari svolgere quesito a); se n6 è dispari svolgere quesito b).
a) Sia z un numero reale tale che z + r = r per OGNI numero reale r. Mostrare (usando gli assiomi
per i numeri reali) che z = 0. Basta scrivere poche righe, ma con giustificazione assiomatica per ogni riga.
b) Sia u un numero reale tale che ur = r per OGNI numero reale r. Mostrare (usando gli assiomi per
i numeri reali) che u = 1.
2.
Con la notazione introdotta sopra, se n5 è pari svolgere quesito a); se n5 è dispari svolgere quesito b).
a) Trovare una “formula chiusa” per
Sn = 1 − 3 + 5 − · · · + (−1)n−1 (2n − 1)
e dare una dimostrazione di tale formula tramite induzione matematica.
a) Trovare una “formula chiusa” per
Sn = 2 − 4 + 6 − · · · + (−1)n−1 2n
e dare una dimostrazione di tale formula tramite induzione matematica.
3.
Con la notazione introdotta sopra, se n4 è pari svolgere quesito a); se n4 è dispari svolgere quesito b).
a) Studiare la funzione f (x) = | tan(x)|. In particolare, dire dove la funzione è derivabile e calcolare la
sua derivata quando esiste. Dire pure dove la seconda derivata esiste e calcolarla quando esiste. Dire dove
la funzione è crescente e dove essa è decrescente, e specificare dove essa è convessa e dove è concava.
b) Studiare la funzione f (x) = | cot(x)|. In particolare, dire dove la funzione è derivabile e calcolare la
sua derivata quando esiste. Dire pure dove la seconda derivata esiste e calcolarla quando esiste. Dire dove
la funzione è crescente e dove essa è decrescente, e specificare dove essa è convessa e dove è concava.
4.
Con la notazione introdotta sopra, se n3 è pari svolgere quesito a); se n3 è dispari svolgere quesito b).
R∞
2
a) Calcolare (in forma concettuale) −∞ e(−t−1) dt.
R∞
2
b) Calcolare (in forma concettuale) −∞ e(−t+1) dt.
5. Con la notazione introdotta sopra, se n6 è ≤ 4 svolgere quesito a); se n6 è ≥ 5 svolgere quesito b).
a) Calcolare la serie di Fourier della funzione f (x) che è periodica con periodo 2π ed è definita da
f (x) =
n
0
1
se −π ≤ x ≤ 0
se 0 < x < π.
b) Calcolare la serie di Fourier della funzione f (x) che è periodica con periodo 2π definita da
f (x) =
n
1 se −π ≤ x ≤ 0
0 se 0 < x < π.
2