3^ lezione
3^ LEZIONE MATEMATICA
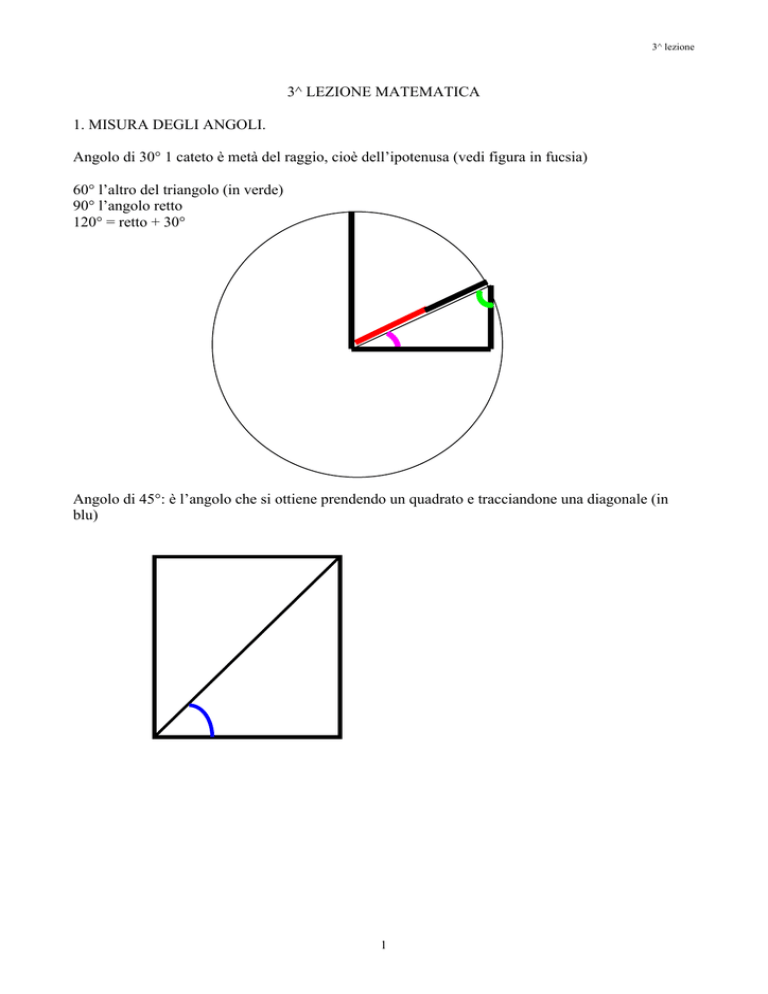
1. MISURA DEGLI ANGOLI.
Angolo di 30° 1 cateto è metà del raggio, cioè dell’ipotenusa (vedi figura in fucsia)
60° l’altro del triangolo (in verde)
90° l’angolo retto
120° = retto + 30°
Angolo di 45°: è l’angolo che si ottiene prendendo un quadrato e tracciandone una diagonale (in
blu)
1
3^ lezione
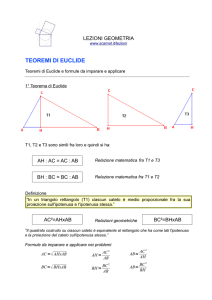
2. Triangoli rettangoli: teoremi di Pitagora ed Euclide
Teorema di Pitagora: a2 = b2 + c2, ovvero il quadrato costruito sull'ipotenusa è la somma dei
quadrati costruiti sui cateti.
1° Teorema di Euclide: b2 = b1·a, c2 = c1·a, ovvero il quadrato costruito su un cateto è
equivalente al rettangolo che ha per lati l'ipotenusa e la proiezione del cateto sull'ipotenusa; o
ancora un cateto è medio proporzionale tra l'ipotenusa e la sua proiezione sull'ipotenusa.
2° Teorema di Euclide: h2 = b1·c1, ovvero il quadrato costruito sull'altezza relativa
all'ipotenusa è uguale al rettangolo che ha per lati le proiezioni dei cateti sull'ipotenusa; o
ancora l'altezza relativa all'ipotenusa è media proporzionale tra le due proiezioni dei cateti
sull'ipotenusa.
Modalità per disegnare un triangolo rettangolo: all’interno di una circonferenza, con
l’ipotenusa sul diametro.
“o se del mezzo cerchio far si puote
triangol sì ch'un retto non avesse.”
Dante Alighieri, Divina Commedia, Paradiso, XIII canto,
versi 101-102
Dante vuol dire che, in una semicirconferenza, prendendo un
lato del triangolo sul diametro (CB) e prendendo un punto A
in modo arbitrario sulla circonferenza, il triangolo ABC è
rettangolo (in A c’è l’angolo retto). AC e AB sono i cateti e
BC è l’ipotenusa.
Inscrivibilità in una semicirconferenza: Un triangolo rettangolo si può sempre inscrivere in
una semicirconferenza; di conseguenza la mediana relativa all'ipotenusa è la metà
dell'ipotenusa ed è il raggio del cerchio circoscritto.
2