ELEMENTI DI EUCLIDE, LIBRO VI:
Le figure simili e le proporzioni in geometria
Richiami dal libro VI di Euclide:
Definizione I del libro VI: due figure poligonali si dicono simili se hanno angoli
uguali e lati che li definiscono corrispondentemente in proporzione.
Proposizione 3 del VI libro: (teorema della bisettrice dell’angolo interno), in un
triangolo la bisettrice di un angolo divide il lato su cui cade in parti proporzionali agli
altri due lati; questa proposizione può anche essere invertita.
Proposizione 6 libro VI: criterio di similitudine tra triangoli
Proposizione 8 libro VI: Primo e secondo teorema di Euclide
Proposizione 10 VI libro (è una costruzione geometrica):
è possibile dividere un segmento in un numero qualunque di parti uguali, usando solo
riga e compasso.
Si noti che questa proposizione generalizza la proposizione 10 del I libro: bisecare
un segmento, mentre La proposizione 9del I libro bisecare un angolo, non può essere
generalizzata: non si può trisecare un angolo con il solo uso di riga e compasso . Per
dimostrare questa impossibilità c'è voluta la teoria di Galois (secolo XIX)
Proposizione 28 VI libro: è data la soluzione dell'equazione di secondo grado, sotto
la condizione che il discriminante sia non negativo.
Proposizione 31 VI libro: generalizzazione del teorema di Pitagora a figure “nei
triangoli rettangoli, la figura costruita sul lato che sottende l'angolo retto è uguale alle
figure simili e similmente costruite sui lati che contengono l'angolo retto”.
TEOREMA DI TALETE
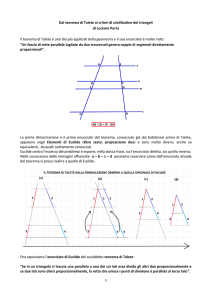
“Un fascio di rette parallele tagliate da due trasversali genera coppie di segmenti
direttamente proporzionali”.
prese tre parallele a,b,c tagliate due rette trasversali r e r’ rispettivamente nei punti
A,B, C e A’, B’, C’, allora il rapporto tra i segmenti omologhi dell’una e dell’altra è
sempre costante:
AB:A’B’ = BC: B’C’
Inoltre
Il teorema di Talete compare negli Elementi di Euclide (proposizione 2 del VI
libro) nella seguente forma:
Se una linea retta è disegnata parallela ad uno dei lati di un triangolo, allora taglia
proporzionalmente i lati del triangolo.
Dimo (prop VI,2):
Euclide dimostra il teorema di Talete indirettamente, mediante le proporzionalità fra
le aree dei triangoli:
Sia dato un triangolo ABC, tagliato da un segmento DE parallelo a uno dei suoi lati
(in questo caso BC). Si ha per la prop VI,2 che
BD:AD=CE:AE
I due triangoli BDE e CDE sono equiestesi, hanno cioè la stessa area, perché hanno
stessa base e stessa altezza. Consideriamo ora l’area del triangolo ADE, si ha:
A(BDE):A(ADE)=A(CDE):A(ADE)
Poiché i triangoli BDE e ADE hanno la stessa altezza uscente dal vertice D, sulle
basi BE e AE rispettivamente si ha anche:
A(BDE):A(ADE)=BD:DA
Analogamente
A(CDE):A(ADE)= CE:EA
Pertanto:
BD:AD=CE:AE .
Nota: dalla proposizione VI,2 segue il teorema di Talete, nel caso in cui le due
trasversali r e s si incontrino in un punto (che corrisponde al vertice A del triangolo
ACB), una volta che esso venga tagliato da più rette parallele al lato opposto ad A.
Se r e s sono parallele tra loro allora la prop VI,2 non si può applicare, ma si usano i
risultati già noti sui parallelogrammi.
Triangoli simili
Come applicazione del teorema di Talete si trovano i criteri di similitudine dei
triangoli (la definizione di similitudine di Euclide è riportata sopra).
primo criterio di similitudine dei triangoli :
Due triangoli, aventi ordinatamente angoli congruenti, sono simili.
secondo criterio di similitudine dei triangoli :
Due triangoli, aventi coppie di lati proporzionali e l’angolo loro compreso
congruente, sono simili.
terzo criterio di similitudine dei triangoli :
Due triangoli, aventi ordinatamente lati in proporzione, sono simili.
Primo teorema di Euclide:
In un triangolo rettangolo il cateto è medio proporzionale tra l'ipotenusa e la
proiezione del cateto stesso sull'ipotenusa.
AC:BC = BC: CH
Ovvero: BC2=AC .CH
Dimo:
Basta osservare che i triangoli ABC e BCH hanno tutti gli angoli congruenti, quindi
sono simili .
Secondo teorema di Euclide:
In un triangolo rettangolo, l'altezza relativa all'ipotenusa è media proporzionale tra le
proiezioni dei cateti sull'ipotenusa.
CH:BH = BH: HA
Ovvero: BH2=CH.HA
Dimo:
Basta osservare che i triangoli BCH e ABH sono simili, perché gli angoli HCB e
ABH sono congruenti, in quanto BAH è complementare di BCA.
Nota: negli Elementi il teorema di Pitagora precede i teoremi di Euclide, ed entrambi
dipendono dal quinto postulato (si tratta di usare rette parallele, univocamente
definite). Ci sono dimostrazioni dei teoremi di Euclide che usano il teorema di
Pitagora, ed è lecito, e ci sono dimostrazioni del teorema di Pitagora che usano i
teoremi di Euclide, in questo caso dovremmo assicurarci che il teorema di Pitagora
non viene utilizzato a sua volta per dimostrare i teoremi di Euclide, né i criteri di
similitudine, ovvero il teorema di Talete, altrimenti si produce un cortocircuito logico.