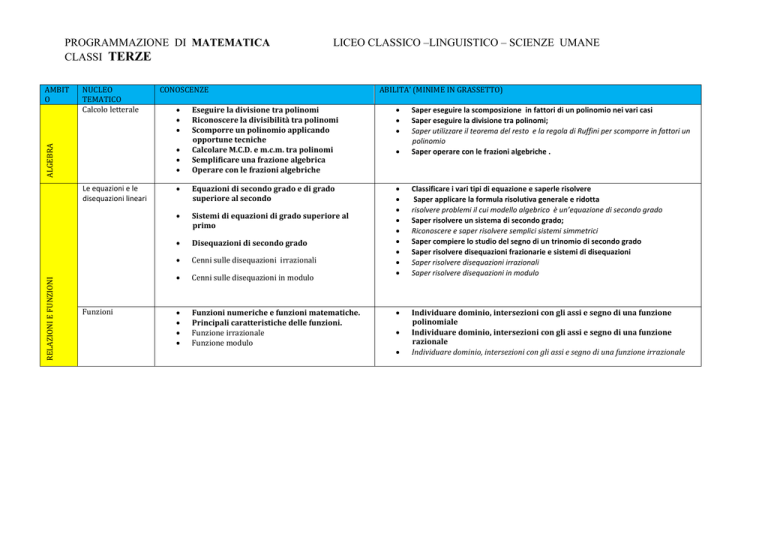
PROGRAMMAZIONE DI MATEMATICA
CLASSI TERZE
NUCLEO
TEMATICO
Calcolo letterale
ALGEBRA
AMBIT
O
RELAZIONI E FUNZIONI
CONOSCENZE
Funzioni
ABILITA’ (MINIME IN GRASSETTO)
Eseguire la divisione tra polinomi
Riconoscere la divisibilità tra polinomi
Scomporre un polinomio applicando
opportune tecniche
Calcolare M.C.D. e m.c.m. tra polinomi
Semplificare una frazione algebrica
Operare con le frazioni algebriche
Saper eseguire la scomposizione in fattori di un polinomio nei vari casi
Saper eseguire la divisione tra polinomi;
Saper utilizzare il teorema del resto e la regola di Ruffini per scomporre in fattori un
polinomio
Saper operare con le frazioni algebriche .
Equazioni di secondo grado e di grado
superiore al secondo
Sistemi di equazioni di grado superiore al
primo
Disequazioni di secondo grado
Cenni sulle disequazioni irrazionali
Cenni sulle disequazioni in modulo
Classificare i vari tipi di equazione e saperle risolvere
Saper applicare la formula risolutiva generale e ridotta
risolvere problemi il cui modello algebrico è un’equazione di secondo grado
Saper risolvere un sistema di secondo grado;
Riconoscere e saper risolvere semplici sistemi simmetrici
Saper compiere lo studio del segno di un trinomio di secondo grado
Saper risolvere disequazioni frazionarie e sistemi di disequazioni
Saper risolvere disequazioni irrazionali
Saper risolvere disequazioni in modulo
Funzioni numeriche e funzioni matematiche.
Principali caratteristiche delle funzioni.
Funzione irrazionale
Funzione modulo
Individuare dominio, intersezioni con gli assi e segno di una funzione
polinomiale
Individuare dominio, intersezioni con gli assi e segno di una funzione
razionale
Individuare dominio, intersezioni con gli assi e segno di una funzione irrazionale
Le equazioni e le
disequazioni lineari
LICEO CLASSICO –LINGUISTICO – SCIENZE UMANE
Coordinate
cartesiane e Retta
(richiami)
GEOMETRIA
Circonferenza
Parabola
GEOMETRIA
Ellisse
Coordinate cartesiane sul piano cartesiano.
Punto medio di un segmento.
Baricentro di un triangolo.
Distanza tra due punti.
Area di un triangolo
Equazione lineare in x e y. Forma implicita
della retta.
Condizione di parallelismo e perpendicolarità
tra due rette.
Retta per un punto.
Distanza di un punto da una retta.
Simmetria assiale.
Alcuni luoghi geometrici: asse di un segmento.
La circonferenza come luogo geometrico,
equazione cartesiana ed elementi
caratterizzanti.
Intersezioni di una circonferenza con una
retta. Rette tangenti.
Condizioni per determinare l’equazione di una
circonferenza.
Tracciare il grafico di una circonferenza di data equazione.
Determinare l’equazione di una circonferenza dati alcuni elementi.
Stabilire la posizione reciproca retta-circonferenza e circonferenzacirconferenza.
Determinare l’equazione delle tangenti ad una circonferenza.
Risolvere i problemi di geometria analitica sulla circonferenza.
La parabola come luogo geometrico, equazione
cartesiana ed elementi caratterizzanti.
Equazione della parabola con asse di
simmetria parallelo all’asse y e all’asse x.
Intersezioni di una parabola con una retta.
Rette tangenti.
Condizioni per determinare l’equazione di una
parabola.
Disequazioni di secondo grado con uso della
parabola.
L’ellisse come luogo geometrico.
Equazione e proprietà dell’ellisse.
Intersezione di un’ellisse con una retta e condizione
di tangenza.
Condizioni per determinare l’equazione di
un’ellisse.
Individuare gli elementi caratterizzanti una parabola.
Tracciare il grafico di una parabola di data equazione.
Determinare l’equazione di una parabola dati alcuni elementi
Stabilire la posizione reciproca retta-parabola.
Trovare le rette tangenti ad una parabola.
Risolvere problemi di geometria analitica sulla parabola.
Individuare gli elementi caratterizzanti una ellisse.
Tracciare il grafico di una ellisse di data equazione.
Determinare l’equazione di una ellisse dati alcuni elementi.
Stabilire la posizione reciproca retta-ellisse.
Trovare le rette tangenti ad una ellisse.
Risolvere problemi di geometria analitica sull’ellisse.
Saper determinare le coordinate del punto medio di un segmento e la
distanza tra due punti
Calcolare e utilizzare il punto medio, la lunghezza di un segmento, il
baricentro di un triangolo.
Saper risolvere semplici problemi di geometria analitica
Passare da grafico di una retta alla sua equazione e viceversa.
Individuare, nell’equazione, il coefficiente angolare della retta.
Determinare l’equazione di una retta dati alcuni elementi.
Stabilire la posizione di due rette, anche utilizzando la condizione di
parallelismo e di perpendicolarità.
Calcolare la distanza tra punto e retta.
Calcolare perimetro e area di un triangolo di un poligono.
Determinare l’asse di un segmento.
Iperbole
DATI E
PREVISIONI
Probabilità
L’iperbole come luogo geometrico.
Equazione e proprietà dell’iperbole.
Iperbole equilatera.
Intersezioni di un’iperbole con una retta e
condizioni di tangenza.
Condizioni per determinare l’equazione di
un’iperbole.
L’iperbole traslata.
La funzione omografica.
Individuare gli elementi caratterizzanti una iperbole.
Tracciare il grafico di una iperbole di data equazione.
Determinare l’equazione di una iperbole dati alcuni elementi.
Stabilire la posizione reciproca retta-iperbole.
Trovare le rette tangenti ad una iperbole.
Determinare le equazioni di iperboli traslate.
Tracciare il grafico di iperboli traslate e di funzioni omografiche.
Risolvere problemi di geometria analitica sull’iperbole.
Calcolo combinatorio: combinazioni,
disposizioni, permutazioni
Definizione classica di probabilità
Probabilità totale
Probabilità contraria
Probabilità condizionata
Calcolare la probabilità di eventi semplici
Utilizzare la probabilità della somma logica e del prodotto logico di eventi
Calcolare la probabilità condizionata
PROGRAMMAZIONE DI MATEMATICA
CLASSI QUARTE
.
AMBITO
NUCLEO TEMATICO
Angoli e funzioni goniometriche
GEOMETRIA
RELAZIONI E FUNZIONI
Formule goniometriche
Equazioni e disequazioni
goniometriche
Esponenziali e logaritmi
ALGEBRA
CONOSCENZE
Misura degli angoli
Definizione e rappresentazione
delle funzioni seno, coseno e
tangente.
Rappresentazione delle funzioni
secante, cosecante e cotangente.
I valori delle funzioni
goniometriche di angoli
particolari.
Funzioni goniometriche inverse.
Archi associati.
Formule goniometriche (addizione,
sottrazione, duplicazione, bisezione,
parametriche, prostaferesi, Werner).
Risoluzione dei triangoli con
l’uso della goniometria
LICEO CLASSICO –LINGUISTICO – SCIENZE UMANE
ABILITA’
Saper misurare gli angoli in gradi sessagesimali e in radianti.
Saper individuare gli angoli sulla circonferenza goniometrica.
Conoscere il significato geometrico di seno, coseno e tangente e
cotangente.
Conoscere i valori delle funzioni goniometriche degli angoli notevoli e di
angoli particolari.
Risolvere espressioni goniometriche.
Conoscere definizioni e saper calcolare espressioni con le funzioni
goniometriche inverse
Conoscere le relazioni fra angoli associati e saperle utilizzare nel calcolo
di espressioni.
Saper dimostrare e utilizzare le formule di addizione sottrazione,
duplicazione, bisezione, parametriche, prostaferesi, Werner.
Equazioni goniometriche
elementari.
Equazioni goniometriche lineari ed
omogenee.
Disequazioni goniometriche.
Saper risolvere le equazioni elementari in seno, coseno e tangente .
Saper risolvere le equazioni lineari, omogenee e le disequazioni
goniometriche.
Triangoli rettangoli
Triangoli qualsiasi e teoremi
(corda, dei seni e dei coseni).
Applicazioni (area di un triangolo).
Dimostrare e saper applicare i teoremi sulla risoluzione dei triangoli
rettangoli.
Dimostrare e saper applicare il teorema sul calcolo dell’area di un triangolo
qualsiasi.
Dimostrare e saper applicare i teoremi sui triangoli qualsiasi.
Risolvere problemi.
Conoscere le proprietà delle potenze con esponente intero, razionale,
reale.
Conoscere il grafico della funzione esponenziale.
Saper risolvere semplici equazioni esponenziali.
Conoscere i logaritmi e le loro proprietà e il grafico della funzione
logaritmica.
Saper calcolare il valore di espressioni logaritmiche ed esponenziali.
Saper risolvere semplici equazioni logaritmiche.
Risolvere disequazioni logaritmiche ed esponenziali.
Potenze con esponente reale.
La funzione esponenziale.
Equazioni esponenziali.
I logaritmi e loro proprietà.
La funzione logaritmica.
Equazioni logaritmiche.
Disequazioni esponenziali e
logaritmiche.
DATI E PREVISIONI
Probabilità e calcolo
combinatorio
Disposizioni, permutazioni,
combinazioni.
I coefficienti binomiali.
Probabilità della somma di eventi.
Probabilità condizionata.
Probabilità del prodotto di eventi,
Teorema di Bernoulli, Teorema di
Bayes.
Conoscere le definizioni e saper calcolare le disposizioni semplici e con
ripetizione, le permutazioni semplici e con ripetizione, il fattoriale di un
numero, le combinazioni semplici e con ripetizione, i coefficienti
binomiali.
Conoscere la definizione di probabilità (concezione classica).
Saper definire la probabilità di un evento e dell’evento contrario, la
probabilità della somma di eventi (teorema della probabilità totale), la
probabilità condizionata (teorema), la probabilità del prodotto di eventi
(teorema della probabilità composta).
Conoscere e saper applicare il Teorema di Bernoulli (prove ripetute) e il
Teorema di Bayes .
PROGRAMMAZIONE DI MATEMATICA
CLASSI QUINTE
.
RELAZIONI E FUNZIONI
AMBITO
NUCLEO TEMATICO
LE PROPRIETA’
DELLE FUNZIONI
CONOSCENZE
Le funzioni reali di variabile
reale.
Il dominio il codominio
L’iniettività, la suriettività, la
biettività, l’inversa di una
funzione.
La composizione di funzioni.
La monotonia
Funizioni pari e dispari
LIMITI
Successioni e progressioni.
Funzioni.
Funzioni continue.
IL CALCOLO DEI
LIMITI
Operazioni sui limiti.
Forme indeterminate.
Limiti notevoli
Punti di discontinuità di una
funzione
LICEO CLASSICO –LINGUISTICO – SCIENZE UMANE
ABILITA’
Conoscere le definizioni di dominio e codominio di una
funzione,
Saper rappresentare il grafico di una funzione definita per casi,
Saper individuare dominio e codominio a partire dal grafico di
una funzione,
Saper calcolare il dominio di definizione di funzioni
algebriche (razionali intere e fratte). (cenni ad Irrazionali,
goniometriche, Logaritmiche ed esponenziali solo se studiate le
equazioni e disequazioni)
Conoscere le definizioni e saper riconoscere le proprietà di
iniettività, suriettività e biiettività di una funzione a partire
dal grafico.
Saper calcolare l’espressione della composizione di due funzioni e
conoscere le proprietà dell’operazione.
Conoscere le tipologie di funzioni monotone (crescente,
decrescente).
Conoscere e saper individuare le funzioni pari e dispari.
Conoscere la definizione di successione e il principio di induzione.
Esempi.
Conoscere la definizione di successione convergente e divergente.
Conoscere le progressioni aritmetiche e le relazioni fra i termini.
Esempi.
Conoscere le progressioni geometriche e le relazioni fra i termini.
Esempi.
Conoscere le definizioni di intervalli ed intorni, di punti
isolati e punti di accumulazione.
Conoscere e saper calcolare e saper verificare il limite di una
funzione in un punto finito.
Conoscere la definizione di funzione continua.
Saper calcolare il limite destro e sinistro.
Conoscere la definizione di asintoto verticale.
Conoscere e saper calcolare e saper verificare il limite di una
funzione all’infinito.
Conoscere la definizione di asintoto orizzontale.
Conoscere i teoremi di unicità, permanenza del segno e confronto
Saper calcolare gli asintoti verticali, orizzontali e obliqui di
una funzione razionale.
Saper tracciare il grafico probabile di una funzione razionale
(irrazionale, esponenziale, logaritmica, goniometrica)
Saper riconoscere e classificare i punti di discontinuità di
una funzione a partire dal grafico
Saper calcolare i punti di discontinuità di una funzione
LE DERIVATE
PUNTI STAZIONARI
RELAZIONI E FUNZIONI
INTEGRALI
GEOMETRIA
ANALITICA NELLO
SPAZIO
La derivata di una funzione.
La retta tangente al grafico di
una funzione.
Continuità e derivabilità.
Le derivate fondamentali.
Teoremi sul calcolo delle
derivate: Rolle, Lagrange,
Cauchy, De L’Hopital
La derivate di ordine superiore
Definizione di punti
stazionari
Calcolo di punti stazionari:
massimo, minimo, flesso.
L’integrale indefinito.
L’integrale definito.
Applicazioni degli integrali alla
fisica.
Conoscere il concetto di derivata e significato geometrico
Conoscere e saper calcolare le derivate fondamentali
Saper utilizzare i teoremi sulle derivate per il calcolo di
derivate di funzioni somma, differenza, prodotto, quoziente,
composte.
Saper riconoscere punti stazionari graficamente
Saper determinare i punti stazionari per funzioni semplici
con l’uso delle derivate
Conoscere la differenza tra integrale definito indefinito
Saper calcolare integrali indefiniti
Saper calcolare integrali definiti
Riconoscere le applicazioni degli integrali alla fisica
Le coordinate cartesiane nello
spazio.
Piano.
Retta .
Sfera.
Conoscere e saper usare le formule della distanza tra punti, del
punto medio di un segmento,
Conoscere e saper calcolare l’equazione generale di un piano e di
alcuni piani particolari,
Conoscere la condizione di parallelismo e di perpendicolarità fra
piani,
Conoscere e saper usare la formula della distanza punto-piano,
Conoscere e saper calcolare l’equazione della retta generale e in
altre forme (retta passante per due punti, equazione frazionaria e
parametrica),
Conoscere le condizioni di parallelismo e di perpendicolarità tra
rette
Conoscere e saper calcolare l’equazione di una superficie sferica.












