Geometria del piano come linguaggio formale La

Geometria del piano come linguaggio formale
La geometria non euclidea
Enrico Gregorio
Introduzione
Gli assiomi della geometria enunciati da Euclide sono stati ritenuti, per secoli,
verità evidenti e necessarie. Nel diciannovesimo secolo, questo modo di pensare
è cambiato.
Perché?
Ci sono molti motivi. Il problema delle parallele è stato certamente una
spinta, ma non è l’unico.
Si possono distinguere almeno tre punti di vista, che si ritrovano proprio
nei tre personaggi più importanti nella ideazione della geometria non euclidea:
Gauss, Bolyai e Lobačevskij.
Gauss
Le ricerche di Gauss sul problema delle parallele nascono dai suoi risultati di
geometria differenziale e dal riconoscimento che, su superfici curve, non è sempre
evidente quale sia la linea più breve che congiunge due punti. Se chiamiamo
“rette” queste linee, accadono cose diverse che sul piano. Per esempio, sulla sfera
le linee più brevi sono i cerchi massimi; due cerchi massimi si incontrano sempre,
in due punti. Dunque sulla sfera non è vero che esistono “rette” parallele.
Sul cilindro (quali sono le linee più brevi?) accade qualcosa di più complicato.
Alcune di queste linee si incontrano, altre no. In effetti succede qualcosa di simile
al piano: per un punto esterno a una “retta” si può condurre una “retta” che
non incontra quella data.
Bolyai
János Bolyai camminò secondo la tradizione, ma non prese paura delle conseguenze strane che derivano dall’assumere che la parallela non sia unica. Alcune
sono notevoli. Se la parallela non è unica, non esistono triangoli di area arbitraria: esiste un limite superiore all’area di un triangolo, una volta fissata l’unità
di misura.
Altre stranezze: alcuni cerchi sono quadrabili; in alcuni quadrati la diagonale
è commensurabile con il lato; due triangoli simili sono uguali.
In effetti uno dei punti fondamentali del lavoro di Bolyai era di dimostrare
che, assumendo la non unicità della parallela, alcuni cerchi sono quadrabili.
1
Lobačevskij
La visione della geometria di Lobačevskij era diversa. Cercava infatti di derivare
gli assiomi da concetti primitivi diversi: quelli di corpo e di distanza. Per
esempio definiva un piano come luogo delle intersezioni di due fasci di sfere
concentriche.
Per capirlo forse è meglio pensare al piano usuale. Fissiamo due punti distinti A e B; poi pensiamo a due circonferenze di uguale raggio, una con centro in A
e l’altra con centro in B. Se queste si intersecano, consideriamo i punti di intersezione. Se ora facciamo variare il raggio, i punti che otteniamo appartengono
a una retta e, anzi, sono tutti i punti di quella retta.
Lo stesso faceva Lobačevskij nello spazio per ottenere i piani; da quelli poteva
definire le circonferenze come intersezione di un piano con una sfera e poi le rette
nel piano.
Da nessuno dei suoi assiomi risultava necessario assumere l’unicità della
parallela.
Poincaré e Klein
Le teorie esposte da Bolyai e Lobačevskij sono accettabili?
La domanda non ha un vero senso, se non precisiamo che cosa significa “accettabile”. Se “accettabile” vuol dire “non contraddittorio”, allora la geometria
non euclidea è accettabile.
Questo fu dimostrato da Poincaré e Klein che fornirono modelli della geometria non euclidea all’interno della geometria euclidea. Dunque, se la geometria
euclidea è accettabile, anche quella non euclidea lo è.
Discuteremo di questo punto più avanti. Per ora vediamo che cosa serve
per dire che una teoria è “non contraddittoria”. Dobbiamo necessariamente
formalizzarla, cioè creare un linguaggio formale che la descriva e verificare che,
dai suoi assiomi, non si possono ricavare contraddizioni.
2
Capitolo 1
Un linguaggio formale per
la geometria piana
Cerchiamo un linguaggio formale per descrivere la geometria del piano e nel
quale siano esprimibili gli assiomi euclidei. Di fatto rinunceremo a parecchi degli
assiomi di Hilbert, limitandoci a una trattazione semplificata; scopo di queste
note è di mostrare come si possa formalizzare la geometria in modo analogo a
quanto fatto per l’aritmetica.
1.1
La struttura
L’insieme che vogliamo considerare intuitivamente come universo non è quello
dei punti del piano, come inizialmente si potrebbe pensare. L’insieme adatto
consiste dei punti e delle rette. Introdurremo quindi due relazioni unarie che ci
diranno quando un elemento dell’universo è un punto o una retta.
Come altra relazione binaria avremo l’appartenenza. Avremo anche relazioni ternarie per esprimere il fatto che due punti “stiano nello stesso semipiano
rispetto a una retta” e per esprimere che “un punto di una retta sta fra altri
due punti della stessa retta”.
Introdurremo altre relazioni, quando necessario.
1.2
Il linguaggio
Simboli propri del linguaggio saranno:
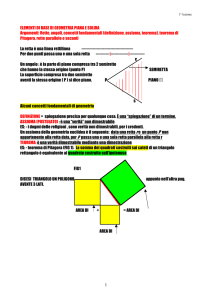
• ‘=’, simbolo di relazione binaria (l’uguaglianza);
• ‘P’, simbolo di relazione unaria (intuitivamente, “è un punto”);
• ‘R’, simbolo di relazione unaria (intuitivamente, “è una retta”);
• ‘A’, simbolo di relazione binaria (intuitivamente, “appartiene alla retta”);
• ‘H’, simbolo di relazione ternaria (intuitivamente, “due punti sono dalla
stessa parte rispetto a una retta”);
3
• ‘F’, simbolo di relazione ternaria (intuitivamente, “un punto sta fra altri
due”).
Prima di proseguire, il lettore è invitato a provare a scrivere gli enunciati
degli assiomi di Euclide in questo linguaggio.
1.3
Assiomi
Considereremo solo strutture nelle quali alcune formule siano interpretate come
vere.
Assioma 1. Solo un punto può appartenere a una retta:
∀v0 ∀v1 →Av0 v1 ∧Pv0 Rv1
Se x appartiene a y, allora x è un punto e y è una retta. Si tratta di un
assioma che semplifica la scrittura degli assiomi seguenti.
Assioma 2. Per due punti passa una retta:
∀v0 ∀v1 →∧Pv0 Pv1 ∃v2 ∧Rv2 ∧Av0 v2 Av1 v2
Possiamo dare la lettura intuitiva: se x e y sono punti, allora esiste una retta
r tale che i punti x e y appartengano a r. Notiamo che, in ogni struttura in cui
questa formula sia vera, ogni punto appartiene ad almeno una retta.
Assioma 3. Su una retta devono esserci almeno due punti distinti:
∀v0 →Rv0 ∃v1 ∃v2 ∧Av1 v0 Av2 v0
La lettura di queste formule diventa molto complicata se non si introducono
abbreviazioni. Perciò ne introdurremo via via.
Assioma 4. Per due punti distinti passa una sola retta:
∀v0 ∀v1 ∀v2 ∀v3 →∧¬=v0 v1 ∧∧Av0 v2 Av1 v2 ∧Av0 v3 Av1 v3 =v2 v3
Se i punti distinti x e y appartengono alle rette r e s, allora r = s.
Abbreviazione 1. retta(xyr) sta per: ∧AxrAyr, dove x, y e r sono termini.
Notiamo che i termini sono solo le variabili, visto che non introduciamo nel
linguaggio alcun simbolo di costante. L’assioma 4 si può allora esprimere
∀v0 ∀v1 ∀v2 ∀v3 →∧¬=v0 v1 ∧retta(v0 v1 v2 )retta(v0 v1 v3 )=v2 v3
Diamo ora gli assiomi di ordinamento, basati sul concetto di “stare fra”.
Uno di questi asserisce l’infinità della retta.
Assioma 5. Se il punto A sta fra B e C, allora A, B e C sono tre punti distinti
di una retta:
∀v0 ∀v1 ∀v2 →Fv0 v1 v2 ∧∃v3 ∧∧Av0 v3 Av1 v3 Av2 v3 ∧∧¬=v0 v1 ¬=v0 v2 ¬=v1 v2
4
Assioma 6. Se il punto A sta fra B e C, allora A sta fra C e B:
∀v0 ∀v1 ∀v2 →Fv0 v1 v2 Fv0 v2 v1
Assioma 7. Se A e B sono punti distinti di una retta, allora esiste un punto
C tale che B sta fra A e C:
∀v0 ∀v1 →¬=v0 v1 ∃v2 Fv1 v0 v2
L’assioma 7 dice che una retta che passa per A e B contiene almeno un punto
oltre B, cioè che è prolungabile indefinitamente. Scambiando A con B vediamo
che è prolungabile in entrambi i versi. Inoltre a ogni retta appartengono infiniti
punti, perché a ogni retta appartengono almeno due punti (assioma 3).
Da questo momento, eviteremo di scrivere gli assiomi come formule e useremo
un linguaggio meno formale. Il lettore può provare a scrivere da sé le formule
necessarie.
Assioma 8. Se A, B e C sono punti distinti di una retta, allora al più uno sta
fra gli altri due.
L’assioma 8 dice che la retta è aperta; si pensi infatti a una circonferenza,
dove non è possibile definire uno “stare fra” (Figura 1.1).
B
A
C
Figura 1.1: Tre punti su una linea chiusa
Assioma 9. Se A, B e C sono tre punti non allineati e r è una retta che non
passa per alcuno di essi ma passa per un punto del segmento AB, allora la retta
r passa per un punto del segmento AC o passa per un punto del segmento BC.
Sembrerà strano che la necessità di questo assioma sia stata riconosciuta solo
alla fine del diciannovesimo secolo, da M. Pasch. Il lettore cerchi di scrivere con
precisione la formula che esprime che una retta passa per un punto del segmento
determinato da due punti.
Il concetto di semipiano, al quale abbiamo legato il simbolo di relazione
ternaria H, serve per definire il concetto di angolo. Non entreremo nei dettagli,
ma scriveremo solo l’assioma che esprime le proprietà dei semipiani.
Assioma 10. Se r è una retta e A e B sono punti distinti del piano non
appartenenti a r, allora A e B sono dalla stessa parte rispetto alla retta r
(formalmente Hv0 v1 v2 , dove v0 sta per A, v1 per B e v2 per r) se e solo se il
segmento AB non contiene punti della retta r.
Come si vede, l’assioma non si scrive in modo molto facile, la formula
richiesta è piuttosto lunga.
C’è un terzo gruppo di assiomi che riguarda la congruenza, ma non li enunceremo. Fra essi si prendono la proprietà transitiva della congruenza fra segmenti
e la proprietà riflessiva della congruenza fra angoli. Come è noto, si usa qui
la parola congruenza per evitare la parola uguaglianza, in modo da non far
assumere ai concetti primitivi significati che non hanno.
5
1.4
Continuità
Un altro gruppo di assiomi è molto importante, quello degli assiomi che parlano
della continuità della retta. Perché lo sono?
Pensiamo alla costruzione con riga e compasso del punto medio di un segmento AB. Con centro in A si traccia la circonferenza di raggio AB e con
centro in B si traccia la circonferenza di raggio BA. Queste due circonferenze
si incontrano in due punti C e D. La retta CD incontra la retta AB nel punto
medio di AB.
Ma è vero che le due circonferenze si incontrano? Usiamo un sistema di
coordinate in cui A sia l’origine e B abbia coordinate (1, 0). Le due circonferenze
hanno equazioni
x2 + y 2 − 1 = 0,
x2 + y 2 − 2x = 0.
Il sistema fra queste due ha soluzioni
√ !
1
2
,
,
2 2
√ !
1
2
,−
2
2
e, senza supporre la continuità della retta, non possiamo dedurre che queste
soluzioni siano coordinate di punti del piano.
Tuttavia parlare della continuità ci porterebbe troppo distante dall’obiettivo
di queste note, che è di discutere dei modelli della geometria non euclidea.
1.5
L’assioma delle parallele
Dagli assiomi precedentemente enunciati seguono molte proprietà: per esempio si può definire il concetto di rette perpendicolari e dimostrare il seguente
enunciato.
Teorema 1. Se A è un punto e r è una retta, allora esiste una e una sola retta
s passante per A e perpendicolare a s.
Si può allora eseguire una nota costruzione (si veda la Figura 1.2). Si considera una retta r e un punto A non appartenente a essa. Si traccia la perpendicolare p da A alla retta r e poi la perpendicolare s per A alla retta p. Chiamiamo
s
A
r
B
C
p
Figura 1.2: Esistenza della parallela
B il punto in cui la retta p incontra la retta r. Se r e s si incontrassero in
un punto C, per questo punto C passerebbero due perpendicolari alla retta p,
contro il Teorema 1.
6
Teorema 2. Se A è un punto non appartenente alla retta r, allora esiste una
retta s passante per A che non incontra la retta r.
Questo risultato permette di stabilire che rette parallele esistono: abbiamo
trovato una costruzione che permette di tracciarne una passante per un punto
dato.
Problema. Una proprietà che ci aspettiamo del parallelismo è che: se a è
parallela a b e b è parallela a c, allora a è parallela a c.
Il lettore provi ad analizzare questo problema e a dimostrare la proprietà
usando solo la definizione e le proprietà già note.
1.6
Unicità della parallela
Se la parallela b e la parallela c sono state costruite secondo lo schema della
Figura 1.2, allora è chiaro che le rette a e c non si incontrano.
Ma chi ci dice che quella sia l’unica costruzione possibile di rette parallele?
È una, certo. Chi dice che non possiamo trovarne una diversa?
Se abbiamo provato a dimostrare la proprietà transitiva del parallelismo
usando solo la definizione, ci troviamo a dover ammettere che non è facile.
Infatti, non solo non è facile: è impossibile. Lo vedremo parlando di geometria non euclidea.
Ricordiamo infatti che una formula (la proprietà transitiva del parallelismo)
è conseguenza logica di un insieme di formule (i nostri assiomi fino a qui) se e
solo se è vera in ogni struttura. Faremo allora un esempio di una struttura nella
quale sono veri tutti gli assiomi, ma non è vero che la parallela sia unica.
Siamo sicuri che Euclide stesso aveva analizzato il problema con cura. Infatti
le prime proposizioni del suo libro sono dimostrate senza usare l’assioma delle
parallele. Per esempio, molte dimostrazioni sui triangoli sono più facili usando
il fatto che la somma degli angoli è un angolo piatto. Invece Euclide non lo usa
e fa una certa fatica, proprio perché è conseguenza dell’assioma delle parallele.
Lo stesso assioma delle parallele non è enunciato nel modo che si trova spesso:
dato un punto A non appartenente a una retta r esiste una e una sola parallela
s a r passante per A. Invece Euclide lo enuncia più o meno cosı̀:
Due rette che, tagliate da una trasversale, formano angoli la cui
somma è minore di un angolo piatto si incontrano dalla parte in cui
la somma degli angoli è minore di un angolo piatto.
Si può vedere la Figura 1.3 nella quale si deve poi pensare di ruotare la retta
più in alto in senso antiorario. Il punto di incontro si sposta sempre più verso
destra. Quando non ci sarà più intersezione?
Come si vede, la risposta non è chiara. Non è possibile dire che non si avrà
intersezione solo quando la somma degli angoli è un angolo piatto. Cosı̀ Euclide
è stato costretto a prendere questa intuizione come assioma.
Nella formalizzazione è meglio evitare di parlare di somma di angoli e di
“incontrarsi dalla parte dove la somma è minore di un angolo piatto”.
7
Figura 1.3: L’assioma delle parallele secondo Euclide
Assioma 11. Se A è un punto non appartenente alla retta r, allora esiste al
massimo una retta s passante per A che non incontra la retta r.
Insieme al teorema che asserisce l’esistenza (Teorema 2), questo assioma dice
che la parallela è una e una sola.
1.7
Asserzioni equivalenti
Durante i secoli ci sono stati molti tentativi di dimostrare l’assioma delle parallele a partire dagli altri. Nessuno c’è riuscito e ora sappiamo il perché.
Rette equidistanti
Un tentativo fu quello di definire parallele due rette equidistanti. Chiaramente,
in questo modo, la parallela è unica. Ma c’è un problema: il luogo dei punti di
un semipiano equidistanti dalla retta origine del semipiano è una retta?
Dire di sı̀ è equivalente all’assioma delle parallele.
Triangoli simili
In geometria euclidea si possono considerare triangoli simili. Ammettere che
esistano triangoli simili non congruenti è equivalente all’assioma delle parallele.
Somma degli angoli interni
Legendre ha dimostrato la seguente asserzione:
Se esiste un triangolo nel quale la somma degli angoli interni è un
angolo piatto, allora vale l’assioma delle parallele.
8
Area
In geometria euclidea si possono immaginare triangoli di area grande quanto si
vuole. Con gli assiomi di continuità è possibile dare la definizione di area di un
triangolo. Gauss ha dimostrato che:
Se, per ogni area assegnata, esiste un triangolo che ha area maggiore,
allora vale l’assioma delle parallele.
Curiosamente, è possibile dimostrare (senza usare l’assioma delle parallele)
che l’area del cerchio cresce al crescere del raggio.
9
Capitolo 2
La geometria non euclidea
Il primo a considerare l’idea di derivare conseguenze dalla negazione dell’assioma
delle parallele fu Girolamo Saccheri nel diciottesimo secolo. Il suo piano era:
• supporre che non valga l’assioma delle parallele;
• dedurre conseguenze da questo;
• trovare una contraddizione.
Il suo lavoro fu veramente pregevole, ma rovinato dal fatto che credette di
avere trovato la contraddizione. Invece si sbagliava.
2.1
Il quadrilatero di Saccheri
Saccheri partiva da un quadrilatero come in Figura 2.1. Si considerano due
punti A e B sulla retta r; si tracciano le perpendicolari a in A e b in B alla retta
r. Su a e su b si prendono i punti C e D in modo che AC sia congruente a BD.
Per simmetria, i due angoli segnati con la croce sono congruenti.
a
b
C
D
A
B
r
Figura 2.1: Il quadrilatero di Saccheri
Ora, i casi sono tre:
• gli angoli sono acuti;
• gli angoli sono retti;
• gli angoli sono ottusi.
10
La terza eventualità si scarta subito. Infatti già in Euclide si trova la dimostrazione che la somma di due angoli di un triangolo non può superare un
angolo piatto e, di conseguenza, la somma degli angoli interni di un quadrilatero
convesso non può superare due angoli piatti.
La seconda eventualità corrisponde al caso dell’unicità della parallela: Saccheri sapeva che, se accade il secondo caso in un quadrilatero, allora accade in
tutti.
Rimane dunque da trovare una contraddizione partendo dalla prima eventualità, che Saccheri chiama inimica hypothesis anguli acuti (la sua opera, “Euclides
ab omni naevo vindicatus” è scritta in latino; significa “Euclide emendato da
ogni imperfezione”).
Fra le prime conseguenze che trovò fu, per esempio, che la misura dell’angolo dipende dalla lunghezza del segmento AC e che il difetto angolare, cioè la
differenza fra l’angolo piatto e la somma degli angoli interni di un triangolo, è
proporzionale all’area.
Altre conseguenze sono che per tre punti non allineati può non passare alcuna
circonferenza: questo fatto è equivalente all’assioma delle parallele!
Pensò di avere trovato la contraddizione cercata nel comportamento delle
perpendicolari alle rette; purtroppo il suo ragionamento non era corretto.
2.2
Lo sviluppo della geometria non euclidea
Si parte dall’assioma che nega quello delle parallele.
Assioma 12. Esistono una retta r, un punto A non appartenente a r e due
rette a e b passanti per A che non incontrano la retta r.
Tutti gli altri assiomi rimangono esattamente uguali.
Consideriamo allora una retta qualunque r e un punto A non appartenente
a r. Sappiamo che certe rette passanti per A incontrano r e che almeno due
rette passanti per A non la incontrano.
Un momento! L’assioma 12 dice questo per una certa retta e per un certo
punto, non per tutte le rette e tutti i punti. Ma Saccheri e Legendre hanno
dimostrato che basta che l’unicità della parallela non valga per un punto e
una retta perché non valga per tutte. Dunque (assumendo anche tutti gli altri
assiomi) l’assioma 12 è equivalente al seguente teorema.
Teorema 3. Se r è una retta e A è un punto non appartenente a r, allora
esistono almeno due rette a e b passanti per A che non incontrano r.
Immaginiamo allora di cominciare dalla perpendicolare p da A alla retta r e
di farla ruotare in senso antiorario. A un certo momento la retta non incontra
più la retta r. Continuando a ruotare arriveremo alla perpendicolare s a p,
che certamente non incontra r (si veda la Figura 2.2). L’angolo segnato con
la crocetta divide le rette che abbiamo considerato in due classi: quelle interne
all’angolo incontrano la retta r, quelle esterne non la incontrano. La retta a che
separa le due classi si chiama parallela a r passante per A. Ovviamente questa
retta di separazione, cioè la parallela, non incontra r; perché?
Notiamo che c’è la retta simmetrica ad a rispetto alla retta p ha la stessa
proprietà nell’altro semipiano. Dunque esistono due rette che si possono chiamare parallele a r passanti per A. Però ci sono infinite rette passanti per A
11
A
s
a
r
Figura 2.2: Angolo di parallelismo
che non incontrano r: la definizione di parallela non è più “una retta che non
incontra r”.
Una conseguenza di tutto questo è che ci sono due versi del parallelismo. Si
può dimostrare (ma non è molto facile) il risultato seguente.
Teorema 4. Se a è parallela a b in un certo verso e b è parallela a c nello stesso
verso, allora a è parallela a c nello stesso verso.
c
b
a
Figura 2.3: Transitività del parallelismo
C’è un problema a guardare figure come la Figura 2.3: che non siamo abituati
a pensare in modo non euclideo. Se evitiamo di pensare che la retta b incontri
la retta a, come saremmo portati a fare, ma che sia parallela a essa (secondo la
definizione), e che la c sia parallela a b, quindi anche ad a allora vediamo subito
il fatto che l’angolo di parallelismo dipende dalla lunghezza di un segmento.
Questo angolo di parallelismo diminuisce al crescere della lunghezza e, quando
questa lunghezza diventa grandissima, l’angolo diventa piccolissimo.
Per motivi di continuità, esisterà un punto A esterno alla retta r tale che
l’angolo di parallelismo sia metà di un angolo retto. Questa è il fatto forse più
sorprendente della geometria non euclidea:
Esiste una unità di misura naturale delle lunghezze.
Per esempio possiamo prendere proprio un segmento in modo che l’angolo di
parallelismo sia esattamente metà dell’angolo retto. Questa unità di misura è
definita in modo assoluto, solo da proprietà geometriche.
In geometria euclidea non è possibile trovare una lunghezza campione definibile in modo assoluto e, se ci pensiamo, il motivo è che dato un triangolo ne
12
possiamo pensare un altro simile a esso e di grandezza arbitraria. In geometria
non euclidea non esistono triangoli simili che non siano uguali.
Definiamo più precisamente l’angolo di parallelismo. Se ci riferiamo alla
Figura 2.2, possiamo indicare con x la misura del segmento di perpendicolare
da A alla retta r; sia Π(x) la misura dell’angolo che la retta parallela a forma
con la perpendicolare. Si può dimostrare che
Π(x)
tan
= e−x/k ,
2
dove k è un numero reale positivo. Questa è la formula dimostrata per la prima
volta da Lobačevskij e Bolyai.
La costante k è caratteristica di tutte le formule della geometria non euclidea.
Prendiamo una situazione in cui x è molto piccolo rispetto a k. Allora x/k
è vicino a zero, quindi e−x/k è vicino a 1 e dunque Π(x) è vicino a un angolo
retto!
Che cosa significa questo? Che se ci limitiamo a una regione molto piccola
dello spazio, la geometria non euclidea è indistinguibile da quella euclidea. Infatti Gauss provò a misurare gli angoli interni di un triangolo, prendendo come
vertici le cime di tre montagne lontane fra loro. Che cosa concluse? Entro gli
errori sperimentali la somma degli angoli è un angolo piatto.
Questo non vuol dire che la geometria dello spazio è euclidea. Al massimo
il risultato può essere interpretato dicendo che la costante k è grande rispetto
alle misure di quelle distanze. Ma non possiamo andare oltre; se consideriamo
triangoli più grandi, con stelle, per esempio, gli errori sperimentali diventano
maggiori.
2.3
Il modello di Klein
Vogliamo trovare un’interpretazione del linguaggio della geometria del piano
nella quale tutti gli assiomi che abbiamo enunciato siano veri. Come assioma
delle parallele prenderemo l’Assioma 12.
Fisseremo una circonferenza Γ del piano euclideo.
2.3.1
I punti e le rette
Gli elementi dell’universo sono i punti interni alla circonferenza Γ e le corde della
stessa circonferenza (Figura 2.4). Abbiamo disegnato qualche punto e qualche
Γ
Figura 2.4: L’universo della struttura.
retta; ricordiamo che gli elementi dell’universo devono essere sia punti che rette.
13
2.3.2
Uguaglianza
Il simbolo di relazione ‘=’ è interpretato come sempre con l’identità.
2.3.3
Punti
Il simbolo di relazione ‘P’ è interpretato come “essere un punto interno a Γ.
2.3.4
Rette
Il simbolo di relazione ‘R’ è interpretato come “essere una corda di Γ”.
2.3.5
Appartenenza
Il simbolo di relazione ‘A’ è interpretato come “il punto appartiene alla corda”.
2.3.6
Semipiani
Il simbolo di relazione ‘H’ è interpretato come “i due punti stanno dalla stessa
parte della retta su cui giace la corda”.
2.3.7
Stare fra
Il simbolo di relazione ‘F’ è interpretato come “il punto sta fra gli altri due,
come nella geometria euclidea, ma solo per i punti interni a Γ.
È un facile esercizio mostrare che tutti gli assiomi che abbiamo enunciato sono veri in questa struttura. Illustriamo l’Assioma 12 con la Figura 2.5. Abbiamo
Γ
Figura 2.5: L’assioma delle parallele non euclideo.
segnato una retta (quella più in basso), un punto e due rette che non incontrano
la retta data. Quella che “sembra” incontrarla è una parallela (nella definizione
della geometria non euclidea); infatti il punto euclideo dove si incontrano non
appartiene alla nostra struttura perché sta sulla circonferenza Γ.
2.4
La distanza nel modello di Klein
Potrebbe rimanere un’incertezza: che nella struttura che abbiamo considerato
non si possano verificare gli assiomi della congruenza. Non abbiamo lo spazio
per trattarli, ma vogliamo vedere come è possibile definire una distanza nel
modello di Klein.
14
Consideriamo quattro punti distinti A, B, C e D di una retta. Ora stiamo
parlando della retta euclidea; su questa retta fissiamo un ordinamento e quindi
parleremo di misure con segno per i segmenti.
Definiamo il birapporto di questi quattro punti come
(ABCD) =
m(AC) · m(BD)
m(AD) · m(BC)
dove m(XY ) denota la misura con segno del segmento XY . Se fissiamo sulla retta un sistema di ascisse, nel quale le ascisse di A, B, C e D sono rispettivamente
a, b, c e d, avremo
(c − a)(d − b)
.
(ABCD) =
(d − a)(c − b)
Vediamo come cambia il birapporto permutando i quattro punti. Le possibili permutazioni
sono 24. Per prima cosa, osserviamo che se scambiamo fra loro A con B e C con D il birapporto
non cambia (cambiano i segni sia di numeratore che di denominatore). Analogamente se
scambiamo A con C e B con D e di nuovo scambiamo le coppie ottenute.
Ponendo r = (ABCD) abbiamo allora
(ABCD) = (CDAB) = (BADC) = (DCBA) = r.
Se invece scambiamo solo A con B, il birapporto si inverte:
(BACD) = (CDBA) = (ABDC) = (DCAB) =
1
.
r
Se scambiamo B con C, abbiamo invece
(ACBD) = (BDAC) = (CADB) = (DBCA) = 1 − r.
Mettendo insieme con i precedenti, abbiamo allora
(ADBC) = (BCAD) = (CBDA) = (DACB) = 1 −
1
r−1
=
,
r
r
1
,
1−r
r
.
(DABC) = (BCDA) = (ADBC) = (CBAD) =
r−1
(CABD) = (BDCA) = (ACDB) = (DBAC) =
Se scriviamo l’espressione esplicita del birapporto quando C = A, otteniamo evidentemente 0; questo è in accordo con il fatto che
(CBAD) =
r
r−1
che vale per r = 0.
Analogamente, se B = A l’espressione per il birapporto dà 1, in accordo con il fatto che
(BACD) =
1
.
r
Se vogliamo considerare il caso di A = D siamo in imbarazzo: l’uguaglianza da soddisfare,
siccome
(DBCA) = 1 − r,
sarebbe r = 1 − r, mentre l’espressione (ABCA) non ha senso perché il denominatore è 0.
Poniamo allora (ABCA) = ∞. Vogliamo che valgano ancora le regole sulle permutazioni dei punti; quindi, siccome (ABDC) = 1/(ABCD) e abbiamo già posto (ABAD) = 0,
dobbiamo porre 1/∞ = 0.
Poiché (DBCA) = 1 − (ABCD), dobbiamo porre 1 − ∞ = ∞.
Poiché (ADBC) = 1 − 1/(ABCD) e abbiamo già posto (AACD) = 1, dobbiamo porre
1 − 1/∞ = 1, che è in accordo con 1/∞ = 0.
Poiché (DBAC) = 1/(1 − (ABCD)) e abbiamo già posto (ABAD) = 0, dobbiamo porre
1/(1 − ∞) = 0 (che ancora va in accordo con le regole 1 − ∞ = ∞ e 1/inf ty = 0).
15
Poiché infine (ADBC) = (r − 1)/r e abbiamo posto (AACD) = 1, dobbiamo porre
(∞ − 1)/∞ = 1.
Non daremo significato a nessun’altra espressione contenente il simbolo ∞.
A che ci serve il birapporto? Sembrerà strano, ma serve proprio a definire
una distanza nel modello di Klein (oltre a tante altre cose). Supponiamo di
avere tre punti A, B e C di una corda U V della circonferenza Γ. Supponiamo
che i punti siano in quest’ordine (Figura 2.6). Ora è piuttosto facile dimostrare
Γ
U
A
B
C
V
Figura 2.6: Birapporti.
che:
(ACU V ) = (ABU V )(BCU V )
e questo dà il modo di definire la distanza cercata:
mK (AB) = | log(ABU V )|
in modo che
mK (AC) = mK (AB) + mK (BC).
Si provi che il limite di mK (AB) è infinito, quando il punto B si avvicina al
punto V .
16