Approfondimento 4.10
La valutazione statistica di skewness e curtosi
Quando si valuta la distribuzione delle risposte ad item di tipo Likert, oltre alla valutazione visiva
della forma della distribuzione in base all’istogramma, ci si basa anche sulle statistiche descrittive
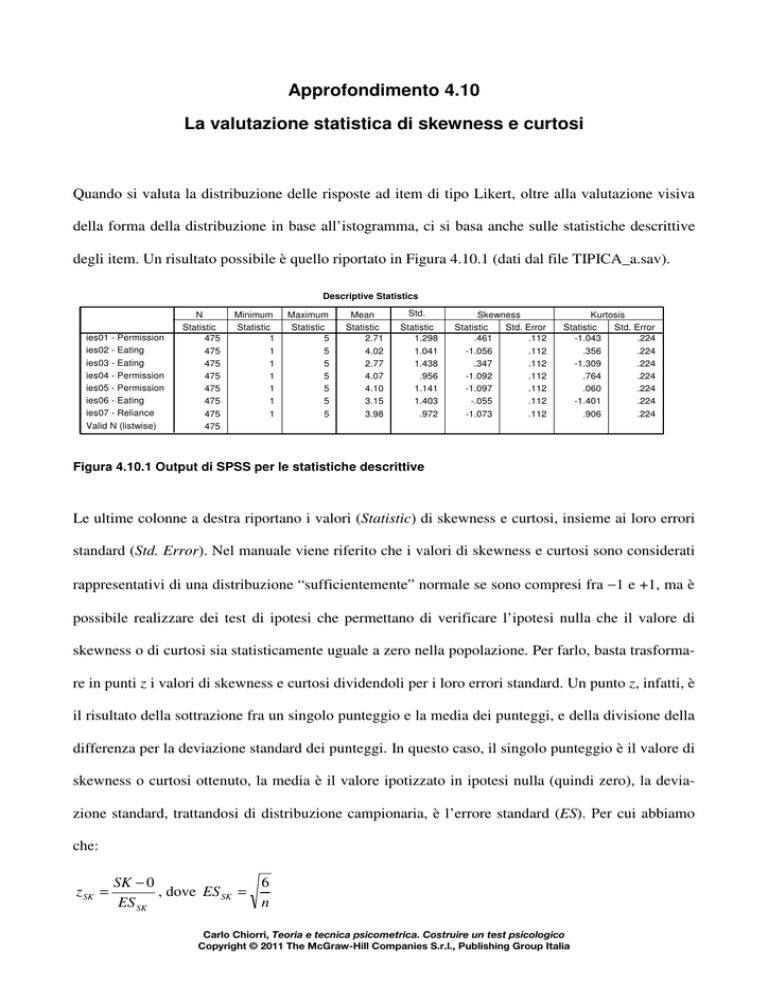
degli item. Un risultato possibile è quello riportato in Figura 4.10.1 (dati dal file TIPICA_a.sav).
Descriptive Statistics
ies01 - Permission
ies02 - Eating
ies03 - Eating
ies04 - Permission
ies05 - Permission
ies06 - Eating
ies07 - Reliance
Valid N (listwise)
N
Statistic
475
475
475
475
475
475
475
475
Minimum
Statistic
1
1
1
1
1
1
1
Maximum
Statistic
5
5
5
5
5
5
5
Mean
Statistic
2.71
4.02
2.77
4.07
4.10
3.15
3.98
Std.
Deviation
Statistic
1.298
1.041
1.438
.956
1.141
1.403
.972
Skewness
Statistic
Std. Error
.461
.112
-1.056
.112
.347
.112
-1.092
.112
-1.097
.112
-.055
.112
-1.073
.112
Kurtosis
Statistic
Std. Error
-1.043
.224
.356
.224
-1.309
.224
.764
.224
.060
.224
-1.401
.224
.906
.224
Figura 4.10.1 Output di SPSS per le statistiche descrittive
Le ultime colonne a destra riportano i valori (Statistic) di skewness e curtosi, insieme ai loro errori
standard (Std. Error). Nel manuale viene riferito che i valori di skewness e curtosi sono considerati
rappresentativi di una distribuzione “sufficientemente” normale se sono compresi fra −1 e +1, ma è
possibile realizzare dei test di ipotesi che permettano di verificare l’ipotesi nulla che il valore di
skewness o di curtosi sia statisticamente uguale a zero nella popolazione. Per farlo, basta trasformare in punti z i valori di skewness e curtosi dividendoli per i loro errori standard. Un punto z, infatti, è
il risultato della sottrazione fra un singolo punteggio e la media dei punteggi, e della divisione della
differenza per la deviazione standard dei punteggi. In questo caso, il singolo punteggio è il valore di
skewness o curtosi ottenuto, la media è il valore ipotizzato in ipotesi nulla (quindi zero), la deviazione standard, trattandosi di distribuzione campionaria, è l’errore standard (ES). Per cui abbiamo
che:
z SK =
6
SK − 0
, dove ES SK =
ES SK
n
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.10 – La valutazione statistica di skewness e curtosi
z KU =
KU − 0
, dove ES SK =
ES KU
2
24
n
Per decidere se è troppo improbabile che sia vera l’ipotesi nulla che il valore di skewness o curtosi
sia uguale a zero nella popolazione fissiamo un livello di probabilità (ad esempio α=,05) e individuiamo il corrispondente valore di z critico per ipotesi alternativa bidirezionale [nel caso α=,05, z
critico = ±1,96; in Excel =INV.NORM.ST(,025)].
Se calcoliamo i valori di z per l’item ies01, otteniamo che:
z SK −ies 01 =
0,461 − 0
= 4,12
0,112
z KU −ies 01 =
− 1,043 − 0
= −4,66
0,224
In entrambi i casi, il valore di z calcolato, in valore assoluto, è maggiore dello z critico, per cui saremmo portati a rifiutare l’ipotesi nulla e ad accettare quella alternativa che i valori di skewness e
curtosi non siano uguali a zero nella popolazione. Il problema, con questo tipo di test statistico, è
che l’ampiezza campionaria ha un peso enorme nel risultato: il campione sul quale stiamo lavorando, infatti, è composto da 475 soggetti, e per come è realizzato il test di significatività saremmo portati a considerare inadeguato un valore di skewness che all’interno della gamma compresa fra −1 e
+1.
Nei casi in cui il test statistico è influenzato da un’eccessiva (o troppo ridotta) ampiezza
campionaria, è utile calcolare la dimensione dell’effetto. Nel caso di un test generico z, la dimensione dell’effetto r si calcola:
r=
z
n
Nel caso specifico di skewness e curtosi, la formula si semplifica:
rSK
SK − 0
6
n = SK
=
6
n
rKU
KU − 0
24
n = KU
=
24
n
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.10 – La valutazione statistica di skewness e curtosi
Per l’item ies01 avremo quindi che rSK =
3
0,461
− 1,043
= −0,21
= 0,19 e rKU =
6
24
Presi in valore assoluto, i due valori di r possono essere interpretati in base alle linee guida di Tabella 4.10.1.
Tabella 4.10.1 Linee guida per l’interpretazione della dimensione dell’effetto r
Valore assoluto di r
< 0,10
0,10 < r < 0,30
0,30 < r < 0,50
r > 0,50
Dimensione dell’effetto
Trascurabile
Piccola
Moderata
Grande
La dimensione dell’effetto è dunque piccola sia per la skewness che per la curtosi dell’item ies01, il
che significa che c’è una deviazione da zero, ma che non appare così rilevante come invece farebbe
pensare il test di significatività.
Una situazione simile si verifica se si applica il test di normalità di Fisher (Kanji, 2006)1.
Tale test si basa sull’elevare al quadrato i valori di skewness e curtosi trasformati a punti z, sommarli e confrontare il risultato con un valore di chi-quadrato critico con due gradi di libertà − la distribuzione chi-quadrato, si ricorda, non è altro che la distribuzione di probabilità che si ottiene elevando la quadrato i punti z e sommandoli. L’ipotesi nulla è che nella popolazione la distribuzione dei
punteggi nell’item sia normale, e quindi si dovrebbe ottenere un valore di chi-quadrato uguale a zero.
Se fissiamo il livello di significatività α a ,05, il chi-quadrato critico è 5.99 [in Excel =
INV.CHI(,05;2)]. Calcoliamo il chi-quadrato calcolato per l’item ies01:
X2(ies01) = (4,12)2 + (−4,66)2 = 38,69
Il valore di chi-quadrato calcolato è superiore a quello di chi-quadrato critico, il che, nuovamente, ci
porterebbe a rifiutare l’ipotesi nulla che la distribuzione dei punteggi nella popolazione sia normale.
Anche il test del chi-quadrato, però, è noto essere pesantemente influenzato dall’ampiezza campionaria. Calcoliamo la dimensione dell’effetto w:
1
Kanji, K. G. (2006). 100 Statistical Test. Londra: Sage.
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.10 – La valutazione statistica di skewness e curtosi
w=
4
X2
38,69
=
= 0,29
n
475
La Tabella 4.10.2 riporta le linee guida per l’interpretazione di questo indice di dimensione
dell’effetto.
Tabella 4.10.2 Linee guida per l’interpretazione della dimensione dell’effetto w
Valore assoluto di w
< 0,10
0,10 < w < 0,30
0,30 < w< 0,50
w > 0,50
Dimensione dell’effetto
Trascurabile
Piccola
Moderata
Grande
Possiamo quindi concludere che lo scostamento da una distribuzione normale dell’item ies01 appare
piccolo.
In generale, quando si valuta la normalità della distribuzione di un item a partire dai valori di
skewness e curtosi, si guarda soprattutto al fatto che essi siano compresi fra −1 e +1. Se invece la
valutazione di skewness e curtosi riguarda il punteggio totale al test, allora è opportuno utilizzare il
test di D’Agostino-Pearson di cui si parla nel Capitolo 6 del manuale.
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia