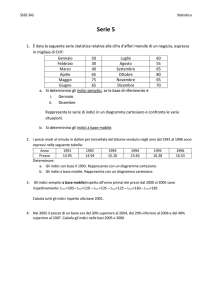
Sintesi dei dati in una tabella
•
•
•
Misure di variabilità (cap. 4)
Misure di forma (cap. 5)
Statistica descrittiva (cap. 6)
Sintesi dei dati
Spesso si vuole effettuare una sintesi dei
dati per ottenere indici che misurino gli
aspetti più rilevanti.
◦ Indici di posizione (misure di tendenza
centrale: medie, mediana, moda, quartili e
percentili cap. 3: scorsa lezione)
◦ Indici di variabilità (cap. 4)
◦ Indici di forma (cap.5)
Le misure (indici) di variabilità
I valori medi (nelle varie forme) condensano i dati in un solo valore
(spesso indicato come centro della distribuzione).
Purtroppo non è sufficiente per rappresentare le osservazioni
effettuate. Quindi si affiancano indici che forniscono informazioni
sulla dispersione, cioè sulla distanza delle osservazioni dal valore
medio.
Minore è la distanza delle osservazioni dal centro
• maggiore è la rappresentatività del valore medio
• minore è la variabilità
Se l’indice di variabilità è nullo allora tutti
i valori sono uguali tra loro.
Per analizzare la distribuzione, occorre:
◦ Calcolare valore medio
◦ Valutare la dispersione:
Calcolare quanto distano le osservazioni dal valore
medio
Calcolare quanto distano i valori tra loro
Vedremo:
Campo di variazione, varianza, scarto quadratico medio
Campo di variazione (range)
E’ la differenza tra l’osservazione più piccola e
quella più grande
In Excel usiamo max e min
Nella cella scriviamo (se A1:E2 è la matrice dati)
=MAX(A1:E2)-MIN(A1:E2)
PROVATE VOI SU UNA
TABELLA PRECEDENTE
Varianza
E’ la media dei quadrati degli scarti dalla media aritmetica
1
n
2
( xi - x )
1
n 1
In Excel usiamo la funzione VAR(num1;num2;…) se gli
argomenti sono un campione della popolazione. Se si tratta di tutta
la popolazione, si usa la funzione VAR.POP
Come sempre, i valori testo e logici sono ignorati. Se si vuole
considerarli, usare la funzione MEDIA.VALORI
PROVATE VOI SU UNA
TABELLA PRECEDENTE
Scarto quadratico medio o deviazione standard
La varianza esprime un indice in funzione del quadrato dell’unità di
misura delle osservazioni.
E’ preferibile calcolare la radice quadrata della varianza, detta
deviazione standard (per mantenere la stessa unità di misura).
=
1
n
2
(
x
x
)
i
n 1 1
In Excel si usa la funzione DEV.ST(num1;num2;…) se gli
argomenti sono un campione della popolazione. Se si tratta di tutta
la popolazione, si usa la funzione DEV.ST.POP
Come sempre, i valori testo e logici sono ignorati. Se si vuole
considerarli, usare la funzione DEV.ST.VALORI
PROVATE VOI SU UNA
TABELLA PRECEDENTE
Sintesi dei dati
Spesso si vuole effettuare una sintesi dei
dati per ottenere indici che misurino gli
aspetti più rilevanti.
◦ Indici di posizione (scorsa lezione; cap. 3)
◦ Indici di variabilità (cap. 4)
◦ Indici di forma (cap.5)
Misure di forma
Si tratta di misure che evidenziano se una
distribuzione è simmetrica rispetto ad un
valore e se risulta più o meno appiattita
Vedremo
Asimmetria e curtosi (appiattimento)
rispetto ad alcune distribuzione note
Asimmetria (skewness)
Indica l’assenza di specularità rispetto all’asse di
simmetria della distribuzione
Esistono diversi indici di asimmetria
Si possono usare media aritmetica, moda e mediana
(x, Mo, Me) per verificare se una distribuzione è
asimmetrica o meno
◦ Se coincidono, è simmetrica
◦ Se Mo<Me< x, è asimmetrica positiva (coda verso destra)
◦ Se x < Me<Mo, è asimmetrica negativa (coda verso sinistra)
Asimmetria in Excel
Usa l’indice di simmetria aF (proposto da Fisher), in cui al denominatore
compare la deviazione standard
Si tratta della funzione
ASIMMETRIA(num1;num2;…)
di almeno 3 argomenti e tale che la deviazione standard sia diversa da zero; se così
non è, viene restituito un errore
◦ aF = 0 simmetrica rispetto la media aritmetica
◦ aF > 0 asimmetrica a destra
◦ aF < 0 asimmetrica a sinistra
Esempio asimmetria positiva
Data la seguente tabella di voti riportati da 18 studenti
N. casi
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
voti
3
4
4
4
4
4
4
4
5
5
5
6,5
6,5
7
7
8
8
9
Analisi dati
Per convenzione, se la coda più lunga è a destra della media (cioè esistono molti valori
con forti scarti positivi e pochi valori con deboli scarti negativi) si parla di asimmetria
positiva e si vuole che il valore dell'indice di asimmetria assuma segno positivo.
Media = 5,4
Asimmetria = 0,61
Il valore di asimmetria è maggiore di zero, quindi la curva si presenta così:
PROVIAMO
Curtosi
Fa riferimento alla maggiore o minore gibbosità di una
distribuzione, in prossimità del suo massimo (e quindi alla
lunghezza delle code)
Per valutare l’aspetto della curva, si paragona ad una curva
«normale» (teorica nota) avente stesse frequenza
complessiva, media e deviazione standard
Si usa un altro indice di Fisher, che coinvolge la deviazione
standard al denominatore: vale 0 se la curva è normale;
positivo o negativo se è più appuntita o meno di una
normale
In Excel è la funzione CURTOSI(num1;num2;…) di
almeno 4 argomenti e tale che la deviazione standard sia
diversa da zero; se così non è, viene restituito un errore
CURTOSI: leptocurtica
In nero la curva «normale» mesocurtica
CURTOSI: platicurtica
distribuzione
platicurtica
In nero la curva «normale» mesocurtica
Principali indici statistici
I grafici finora analizzati ci danno informazioni qualitative; possiamo
quantificarle ricorrendo ai seguenti indici.
Sianox1 , x2 ,..., xn
n osservazioni numeriche
MODA
di posizione
MEDIANA
MEDIA
QUARTILI E PERCENTILI
SCARTO QUADRATICO MEDIO
INDICI
di dispersione
VARIANZA
RANGE
di forma
ASIMMETRIA (SKEWNESS)
CURTOSI ( KURTOSIS)
di dispersione
di posizione
•media:
Indici: Schema riassuntivo
x
x
i
i
N
•moda: punto di max della distribuzione
•mediana: valore sotto al quale cadono la metà dei valori campionari. Si
dispongono i dati in ordine crescente e si prende quello che occupa la posizione
centrale (N dispari) o la media dei 2 valori in posizione centrale (N pari)
•varianza
•deviazione standard
•range
s2
i
s
xi x
2
N 1
R xmax xmin
di di forma
>0 coda a ds
•skewness (coeff. di asimmetria)
<0 coda a sin
=0 simmetrica
•curtosi: misura quanto la distribuzione è appuntita
> 0 più appuntita
< 0 meno appuntita
Statistica descrittiva (cap.6)
Molti indici trattati finora sono generati
automaticamente da Excel, usando Statistica
descrittiva del menù Analisi dei dati.
Proviamo
◦ Etichette nella prima riga/Etichette nella prima
colonna: deselezionarle se l’intervallo non contiene
etichette (altrimenti selezionare quella appropriata,
come nell’esempio 6.3)
Esempio 6.1
PROVIAMO
La tabella seguente riporta il peso in grammi di un campione
di 100 tavolette di cioccolato.
Proviamo a richiamare la funzione Riepilogo statistiche
Media
Errore standard
Mediana
Moda
99,79652336
0,010062453
99,79312502
#N/D
Deviazione standard
Varianza
campionaria
Curtosi
Asimmetria
Intervallo
Minimo
Massimo
Somma
Conteggio
Più grande(1)
Più piccolo(1)
0,100624532
0,010125296
0,083114239
0,069723767
0,484818884
99,55261744
100,0374363
9979,652336
100
100,0374363
99,55261744
Non
esistono
duplicati
Esempio 6.3
PROVIAMO
La tabella seguente riporta la quantità (in quintali) di
semilavorati stoccati in un magazzino negli ultimi 9 anni.
Proviamo a richiamare la funzione Riepilogo statistiche
• selezionare
le celle escludendo la prima colonna
•Etichette nella prima riga/Etichette nella prima
colonna: selezionare l’opzione appropriata